群论笔记 09
Table of Contents
Cat 9.1 Natural transformations
3 most important things in category: 1. definition of category 2. definition of functor 3. definition of natrual transformation
the most most important is (3), (1)(2) is just nessary background knowledge.
category - structure functor - preserve the structure, model a cat in another cat.
compare diff image given by the functors.
natural trans are mappings between functors, — alse preserve the structure.
take into these 2 functor's structure and presever.
so ,what is mapping between functors( remember that, functor is a type constructor with fmap inside )
for objects in Cat C
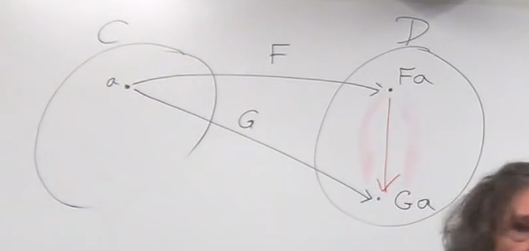
Figure 1: mapping between 2 functors
for other object in C I do the same thing. I find the images of this object and pick a morphism between them.
then I create a whole family of morphisms, these individual morphism is called the component of the natural transformation, — component of /alpha at object of a, notice that object a is in the Cat C, but component /alpha is in Cat D.
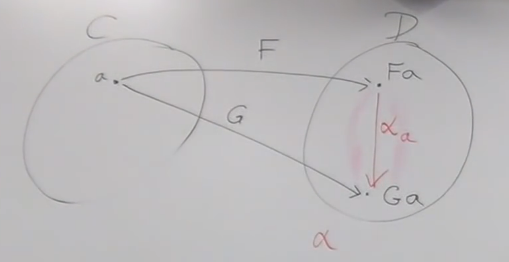
Figure 2: component of natrual trans
- for morphism in Cat C
is there some relation between the Ff and Gf?
[notice] natrual trans is not have to exist between any functors.
we are now pay more attention to the 2 kinds of morphism in Cat D: * the component of NT(relation between two type constructor of same object in C) - in picture below, /alpha\_a : Fa->Ga and /alpha\_b : Fb->Gb * the mophism of original Cat and its mapping in target Cat - in picture below, Ff and Gf
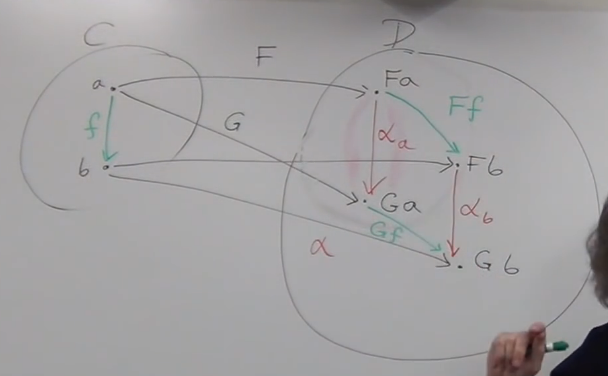
Figure 3: the 'beautiful' Rectangle
Natural transformation describe a mapping between 2 functors, means these two functors are somehow similar, somehow related.So there must be some relations between these 4(2 components and 2 morphism mappings) — THEY ARE COMPOSABLE
α_b * Ff = Gf * α_a
is called Naturality conditoin, and this rectangle is called Naturality Square.
α\_b and α\_a is called Natural Transformation
How Strong is the naturality is ?
that's depends very much on the structure of the category.In some categories there are lots of morphisms between objects like set — morphism rich category.
If we draw these 4 ojbects( set, type constructor ): Fa, Fb, Ga, Gb
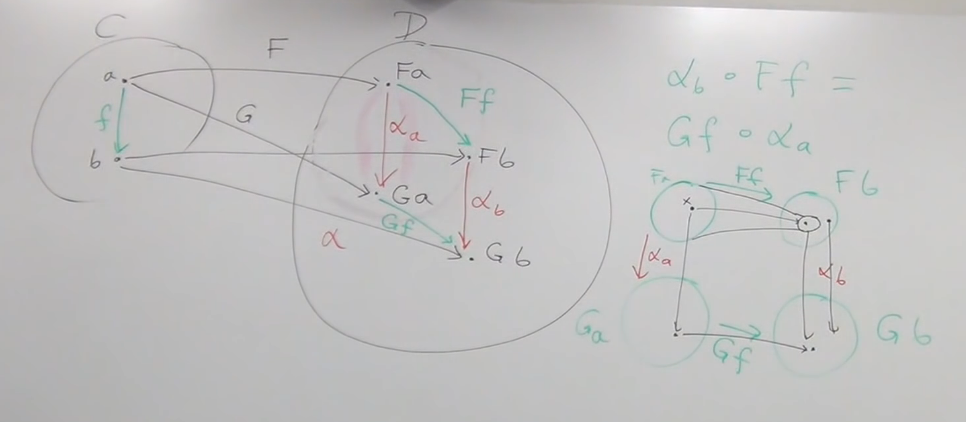
Figure 4: 4 type costructors
Natural trans vs. commutative graph
In mathematics, we often say that: from Cat C, we can find the object a can be mapping to a morphism of Cat D; and similarly, morphism of Cat C can be mapping to a Naturality Squre in Cat D.
natural transformation can be something like higher-level thant the commutative graph. So you just can say "there is a Natural trans between 2 functors", then this means that "there are some commutative graphs,these Naturality squares"
and we will have a second semaster lectures, introducing "limit, colimit" — defined on the basis of Natural trans, of course they also can be defined by the commutative graphs. But Natural Trans is a higher-level 'language' to describe. And we can find that product and coproduct are just special cases of limit and colimit.
components of a Natural Trans are morphisms, and you know that morphisms are functions, function can shrunk information — can lose information. If you map one functor into another functor using a natural trans, there maybe lot of information will lost.
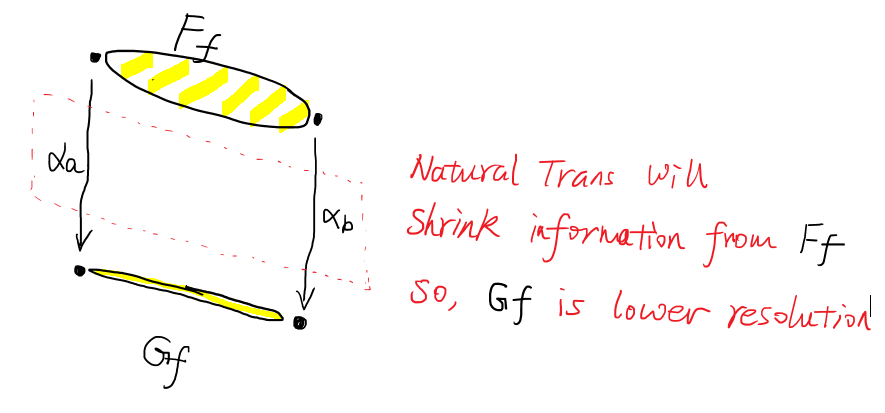
Figure 5: Natural Trans will shrink information
Natural Trans acts like sampling from a high resolutin picture, and get a low resolution picture.
Natural Transformation can invertibel
seriously :| then you find that: you have some mapping, and you have a invertible mapping:
- function and invertible function will lead to a definition of isomorphism, and a isomorphic objects.
- Natural Trans and invertible Natural Trans must will lead to something — isomorphic functors.
so natural transfomation, is also natural isomorphism.
Natural transformation is just a bunch of morphisms, that means there will be bunch of isomorphism.
Move further, means that all of components are invertible morphism, means every component is isomorphism.
Natural isomorphism are really important.
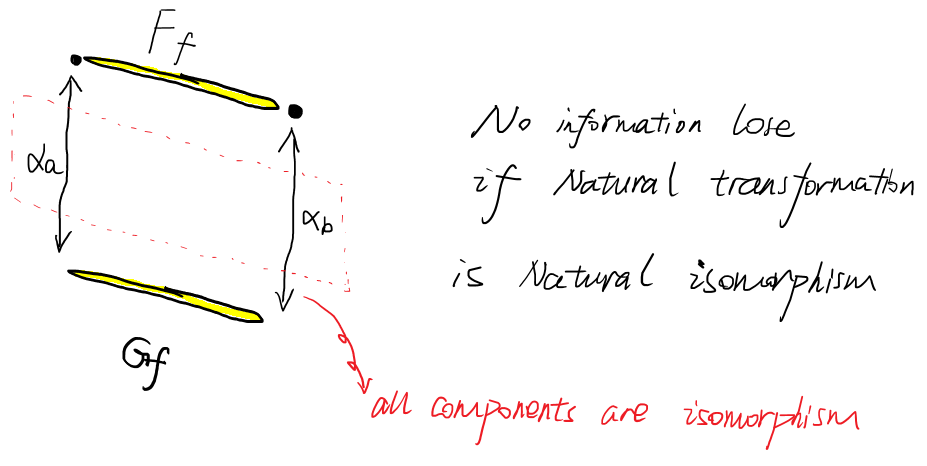
Figure 6: Natural isomorphism
Natural Trans in programming
Functor is mapping between categories, and in Haskell it's endofunctor mapping from ONE category to itself.
Natural transformation is a family of morphisms between two endofunctors.
Family of morphisms, morphism is functin, family of functions that parameterize by a type — which is called polymorphic function.
seriously :|
So,
naturally transformation is a polymorphic function
alpha:: forall a. Fa -> Ga
Notice the difference between polymorphic function and ad-hoc polymorphism. * polymorphic function : apply one function for all type.
ad-hoc polymorphism : (overriding) can apply different function for
different type.
Why I emphasize "apply one function for all types."?
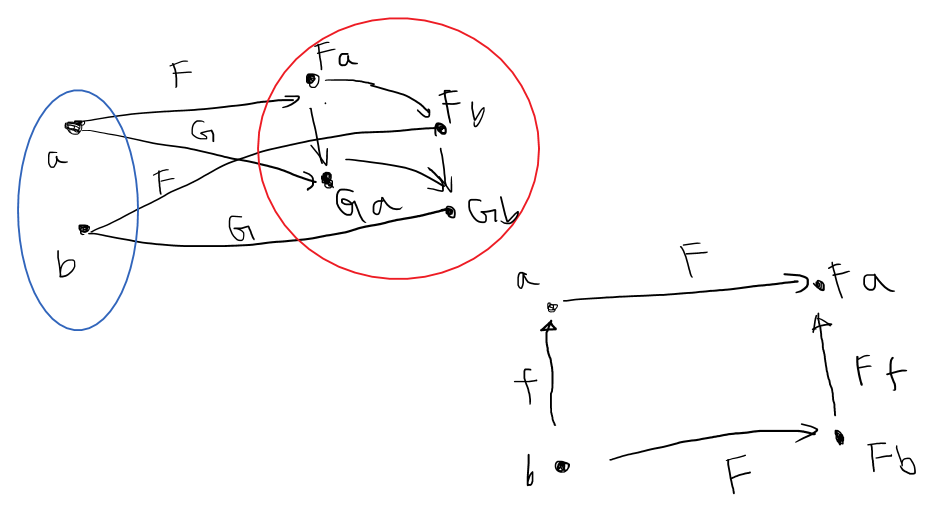
Figure 7: Natural Transform illustration
fmap :: (a->b) -> (Fa->Fb)
alpha:: forall a. Fa -> Ga
α_b * Ff = Gf * α_a
α_b * fmap_F f = fmap_G f α_a is the interpretation of the Naturality
Condition.
Fb->Gb * Fa->Fb = Ga->Gb * Fa->Ga
but α can be applied for all types
or we can say: 1. because of parametric polyphism, Fa->Fb; Ga->Gb; -
like some scala codes List[Int].map() = List[Double] or
Option[String].map() = Option[Int] - every kind of type constructor
will have its own implementation of fmap 2. because of polymorphic
function, Fb->Gb; Fa->Ga - for all type a
alpha:: forall a. Fa -> Ga alpha * fmap f = fmap f * alpha
by the TWO KINDS OF POLYMORPHISM, the naturality condition is automatically satisfied
example
define a safeHead
safeHead :: [a]->Maybe a //this is a F[a]->G[a] a NaturalTransformation safeHead [] = Nothing safeHead (x:xs) = Just x
and it'll automatically find the different implemention of fmap by
different invocator, this scenario List and Maybe. So the whole
naturality condition will automatically satisfied.

Figure 8: naturally condition
How Natural Transformation save lots of computing time
This will give you a intuition that category theory can be used in
programming in a very practical way. You see that from picture above,
apply fmap to a List is very expensive. But if compiler knows
natural transformation, then convert fmap of List, to fmap of a
Maybe, this will save a lot of computing resource
Intuition of functor
So we know that why call a functor a container, because fmap apply to a container will ONLY modify content inside of the container, it will NEVER change the shape of container.
Intuition of natural transformation
On the opposite side, the natural trans NEVER modify the contents of the container, what it ONLY dose is change the shape of the container, repackages the container.
fmap :: (a->b) -> (Fa->Fb)
alpha:: forall a. Fa -> Ga
The ubiquitous of natural transformation
we use polymorphic function a lot, is it a natural transformation?
fn:: a->[a]
function from a to List[a], yes it's a natural transformation:
- type a to type a: is just a identity functor on a
so fn:: a->[a] is truely a natural transformation
fn:: [a]->Int
Like computing the length of a List, it's also a natural transformation,
because the a is constant functor, it will ignore its type argument.
So, in general if you have a polymorphic function from an ADT to
another ADT, it's a natural transformation.
because ADT as showed before, are functors.
Cat 9.2 bicategories
Giving you a large large view of category, as far as professor can do. Diving into deep math.
when you think about mapping, you should ask several questions:
Natural transformation composition
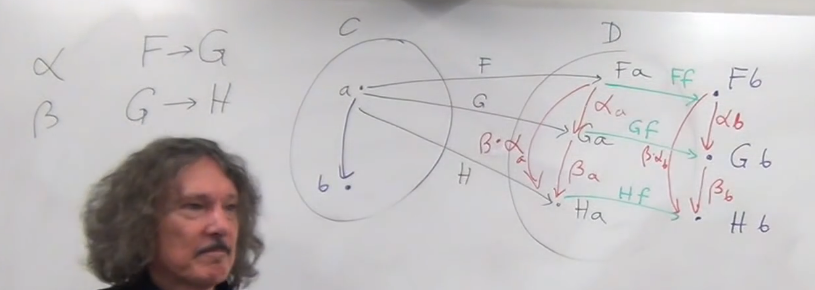
Figure 9: multi-natural transformation
before that we must check the Naturality condition:
Hf * (β * α_a) ? (β * α_b) * Ff=
Diagram chasing, you must make sure all the Naturality condition satisfied.
Composition
of course, NT is bunch of morphism, morphism of course is composable, so dose the NT.
But, hold on, what are we talking about? Mappings of Functors, and Functor is mapping of 2 category.
*when refer to a mapping of some thing, you must ask yourself, can I take this "something" back to the basic concept of "object" of category.*
In this scenario, yes we can:
- NT -> morphism
- functor -> object
- ??? -> category
??? = [C, D]

Figure 11: [C,D] = D\^C
So this scenario: * NT is morphism; * functor is object;
remeber "Category of Category" is a "Cat". remeber that, * functor is the morphism of Cat. * category is the object of Cat.
Cells and 2-category
https://postimg.cc/image/xbly6vrrv/
2-category : has move further one step than "Cat"—category of category, which is the pair category as object.
Hom-set of Cat is set of Functors; Cat often think as a Category of small Category.
Hom-set are trully a set. And then set can be seen as a Category, then we get [C,D] — 2-category.
but wait a minite, in the Category of Category, we have 2 objects: C and D, then [C,D] must also be in the same category with C and D. So:

Figure 12: [C,D] in same Cat with C and D
something like the set: * set = {a,b,c,d} * a ∈ set * c ∈ set * {a,c} ∈ set
Exponential ?

Figure 13: [C,D]
but functor of category, is a exponential ADT,
?????? why [C,D] = D\^C

Figure 14: why [C,D] = D\^C
by the partial function, we can see some glue of [C,D] = D\^C, this should be marked as TODO, I ignore the details of this, when this taught at previous lectures, need reviewing.
categorical products as pairs of elements and categorical products with universal construction and projections, they will give you the same result.
the category of functor category[C,D] is same as the D\^C, we start with a product category CXD,and then do the universal construction and we get the exponential objects.
Can we build something instead hom-sets of hom-objects
vertical composition

Figure 15: vetical composition
Is there the natural trans between G * F and G'*F'

Figure 16: G/F and G'/F'
and the answer is "Yes"

Figure 17: Natural trans between G/F and G'/F'
and it's called β * α.
Interchange law
horizon composition and vertical compoisition

Figure 18: composition of vertical and relation with horizon composition
skipped, too long to draw
but definition of 2-category involves both vertical composition and horizon composition of two cells ,and the interchanging law.
we can get isomorphism from the vertical composition ??? They are called left and right unitor.
2-category vs. bicategory
So, if we start defining the stuff up to isomorphsim, then suddenly from a 2-category we are getting into something called bicategory.
the diff between 2-category and bicategory: * in a bicategory categorical laws are up to isomorphism. * 2-category is more strict than bicategory, becasue categorical laws is equale * bicategory is relaxed version of 2-category.
coherence law
can not understand, so skipped!!
Lets just talk about bicategory
what if we have a category in which all morphism are inverted.If morphism in a category are all inverted, this category is called groupoid.
So if you start doing the same thing with groupoid,instead of categories, turn out that you can have like n-groupoids and coherence laws are simple for groupoids.
so the groupoid people say to catgory people,you're wrong direction. The correct thing to do is work with groupoid, and in particular if you go with high enough, you know at some point you say well, what's wrong with infinity. infinity groupoid.
infinity groupoid would be something has zero cells – objects . one cells morphism between them, two cells morphism between morphims, three cells between morphisms of morphisms and … so on to inifinity.
It turns out this is exactly the structure of the famous homotopy type theory.
homotopy type theory said that groupoid are the way to go, not categories.
