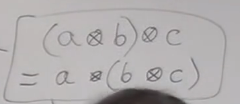群论笔记 10
Table of Contents
Cat 10.1 Monads
Intuition and Definition of monads
Think a basic an important question, why we need function in programming?
we really need functions, because we can structure our program.
we really need functions, because we can decompose and recompose our program.
and both these terms, are the basic concept of our category theory, and is the most important concept in category.
Monad is all about the composing stuff.
. in haskell is used to composint simple function, whose output match
the latter one's input. >=> in hasekll is used to composing function
whose output type is embellished — like logging, with string
embellished inside , the logging are Kleisli arrow.
so we should unpack the return type before we can send it to the next function.
One more step, when we use ">=>" to compose, we can make some decision before composing, maybe we dont want call the next functions at all.
. | >=> |
id | return |
we have a return because we may want some intuision from imperative
programming.
. and id — means identity and composition , can build a category of
functions. >=> and return — means identity and composition , can
build a category of Kleisli.
Signiture of >=>
class Monad m where // m is a type constructor (>>=) :: m a -> (a->mb) -> mb return :: a -> ma // identity Kleisli arrow class Functor m => Monda m where join :: m(ma) -> ma return :: a -> ma // lifting a value
// f g (>=>) :: (a->mb)->(b->mc) -> (a->mc) // m is a functor f >=> g = λ a -> let mb = f a // in ... // in mb >>= g // in ... we must define a function like below // f (>>=):: m a -> (a->mb) -> mb ma >>= f = join (fmap f ma) // m is a functor, it let f unboxing to modify inside and boxing to give back without changing the shape of container. join :: m(ma) -> ma // like List[List] -> List

Figure 1: >=> and >>=
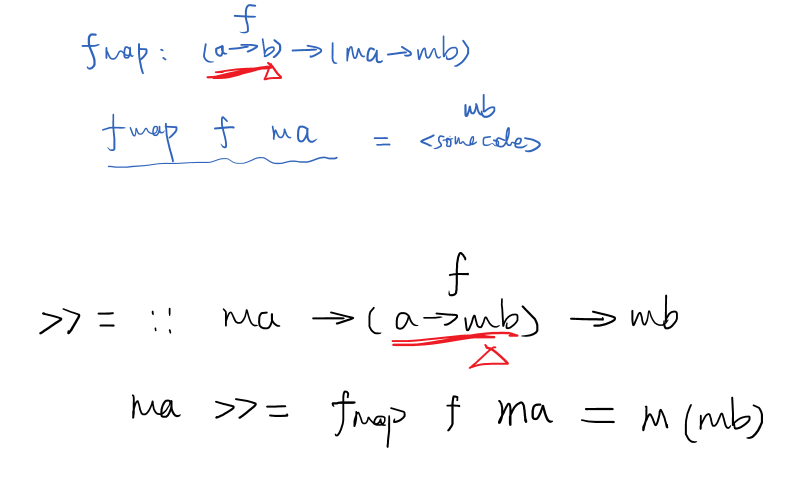
Figure 2: fmap applied to get m(mb)
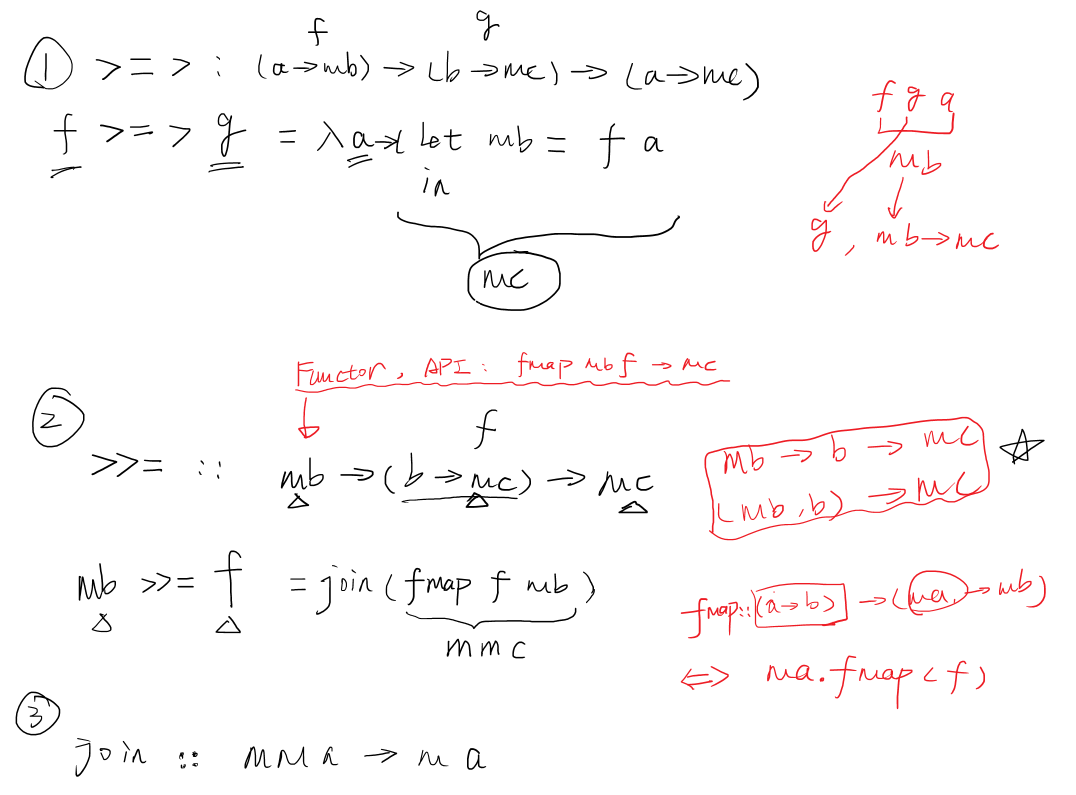
Figure 3: 3 important functions in Monad
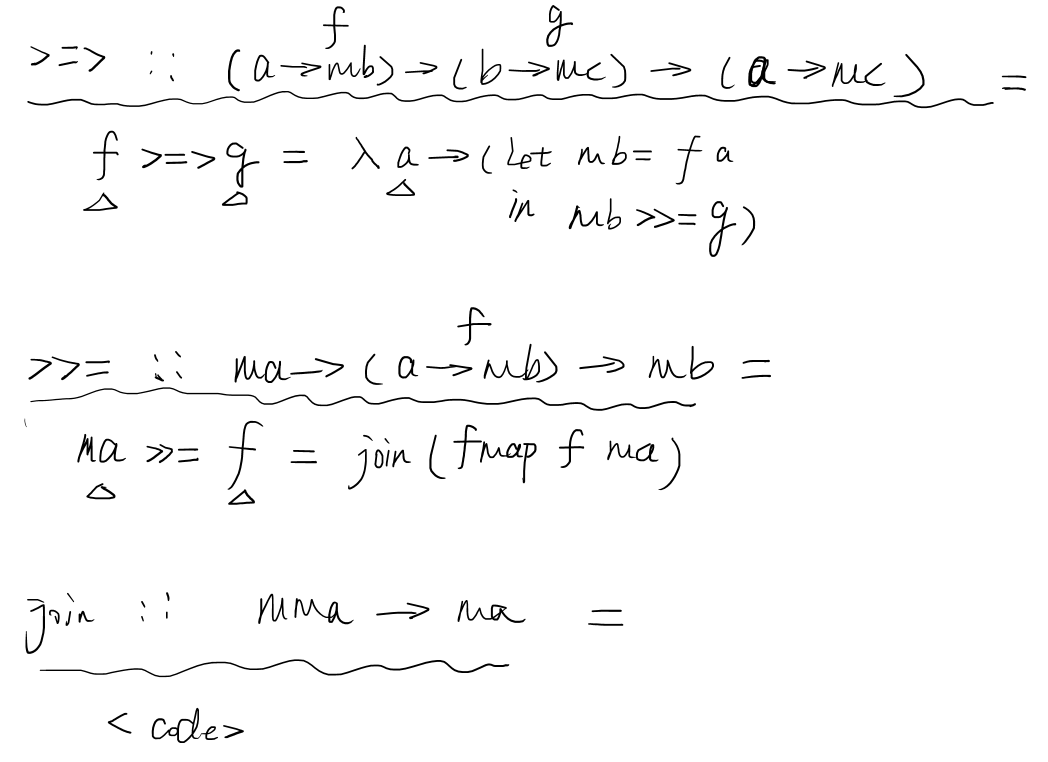
Figure 4: 3 important functions in Monad
note that: type name and variable name are in different name space of Haskell, so we have type name "a" "mb"and a variable in λ function also named "a" "mb", that's OK, no error trigged
>>= is called bind >=> called fish symbol
notice that there is some type-mismatch, and this is where our embellishment come from.
note that: we should not modify the content inside of the container directly, because it's a type variable, we have nothing information about what exactly type it is , so if we want to modify it, we should define extra function to do that.
note that: if you have a monad, you can use join and Kleisli arrow,
they are defined default inside a monad
why we using these monads, what problem they solve
provide composition for Kleisli arrows, but why Kleisli arrows? we have see an example of creating logging things using Kleisli arrows. so really the magical of the monad is not in what monad is — monad is just composition, the magic is why Kleisli arrows is so useful? what kind of problems that they solve?
so it turns out and that was like a big discovery, one paper, and one implemention in Haskell.
In functional programming language, everything is pure function, as a programmer we know that pure functions CANNOT express everything —: * no side effect,but basic input and output is 'side effect', they are not pure * same input must return same output, but when you get a char from stdin, everytime what you get might different. * global state * function with exception * …
these are important.
But, luckyly verything above can be turned into pure calculations *as long as you replace regular functions with functions that return embellished results*. So all the side effects can be translated into some kinds of embellishment of the result of a function and the function remains the pure function. But it produces more than the result, it produces a result that's hidden embellished encapsulated in some way.
The most interesting things is that, when a imperative programmer implement something using impure function ,and a functional programmer comes and says I can do it in pure function — only with output type a little different.*But Monad is still not coming by now.*
If I have a huge nubmer of this kind of functions(from imperative impure to functional pure just with a embellishment of return type), how can I do composing?
or
If I have a biiiiiiiiiiig function of this kind, how can I split them into little pieces.
Then, Monad comes!
Monad says that, you can take this gigantic computations and split into small pieces, do them separately, and compose this stuff. This is Monad.
So, one example of somthing that's usually not done using impure functions is functions that are not defined for all arguments — partial functins. eg, square root is defined ONLY for positive integers,
- you can blow up whole program 2. throw an exception — this is not
functional way, sqroot:: int -> double, but you give an exception type
- return a Maybe — functional way
Examples of Monad
Maybe Monad
a -> b a -> Maybe b
If we have many function of this kind, we can compose them.Let's define join for them.
join:: Maybe(Maybe a) -> Maybe a join ( Just (Just a)) = Just a join _ = Nothing
f :: a-> Maybe b (>>=) :: ma -> (a -> mb) -> mb Nothing >>= f = Nothing Just a >>= f = f a return a = Just a
Nothing >> f = Nothing= acts like a short circuit, if the first f
failed, it will return nothing directly. This is same as a exception.
3 laws have to be satisfied
from introduction above, we know that a Monad must has 3 parts: 1. Functor 2. join 3. return
fish symbol >=> : 1. associative 2. identity(right/left)
3 laws — assoc + right id + left id. have to be satisfied in order to make Kleisli composition.
all these 3 definitions are using category theory, but really everybody
uses the one with join, except things they don't call it with
join,they don't call it with return, they don't call it functor,
or M. They call it T.
remake the symbol of functor and 2 functions
Translation m - T join - μ return - η
These Greek leters — 'μ','η'. are Natural Transformation.
- return is a polymorphic function,
a -> maa -> mais a natural transformation- a — identity functor
- ma — functor too
return function is just a component of Natural transformation:
Id -> T
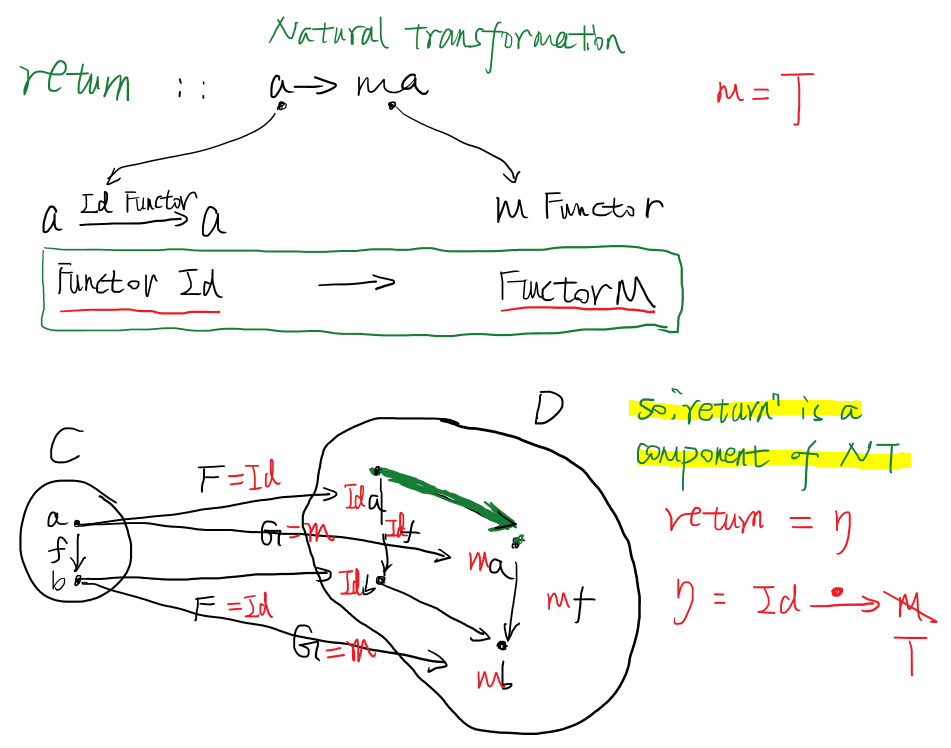
Figure 5: prove return is component of a NT(Functor:Id -> Functor:m)
notation that, picture above has a flaw, T is must be endofunctor means that from C to C, not C to D, because mm:
if m: C->D; then mm:?
so T is endofunctor
join function is just double application of a functor, this is just
the composition of a functor with itself.
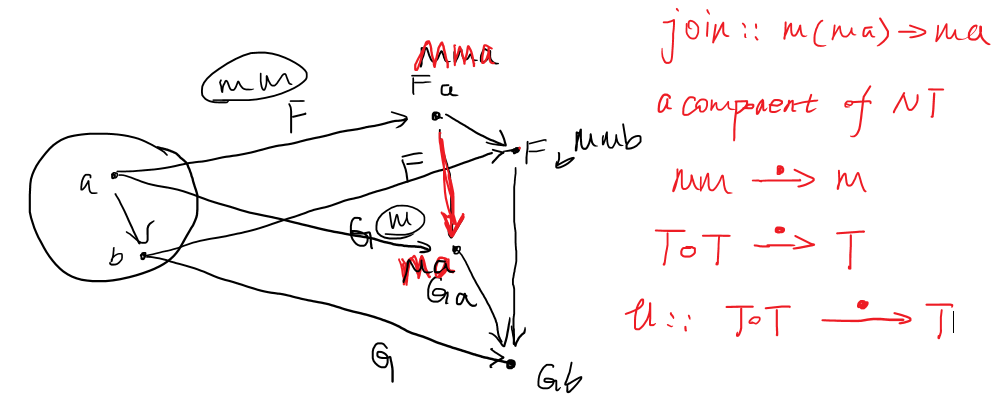 > notation that,
picture above has a flaw, T is must be endofunctor means that from C to
C, not C to D, because mm: > > if m: C->D; > then mm:? > > so T is
endofunctor
> notation that,
picture above has a flaw, T is must be endofunctor means that from C to
C, not C to D, because mm: > > if m: C->D; > then mm:? > > so T is
endofunctor
NT in Category theory vs. NT in Haskell
we dosen't explicitly say something is NT because of polymorphic function, specific NT will automatically decided by the invocatot, which is called "free theory" in haskell.
redefine monad by new symbol
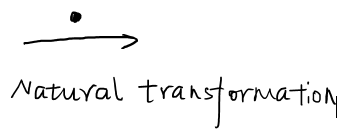
Figure 6: symbol of natural transformation

Figure 7: Natural transformation laws
So monad T, is a functor T and 2 natural transformations eta and
mu, PLUS the 3 laws for these things, else we can not build a
Kleisli category(guarantee the associativity, identity, composibility.)
Monad = T + 2 + 3 Monad = T23
[Notice that] First of all, T is endofunctor, it has to be a endofuncto,if T want from C to D, then we could not apply to T again — join function: T ◦ T -> T.
2-D diagram: composing two NTs in 2 direction
[Notice that] * • in natural transformation is vertical compose * ◦ in natural transformation is horizontal compose
proving law 1: Monad associativity by mu and eta
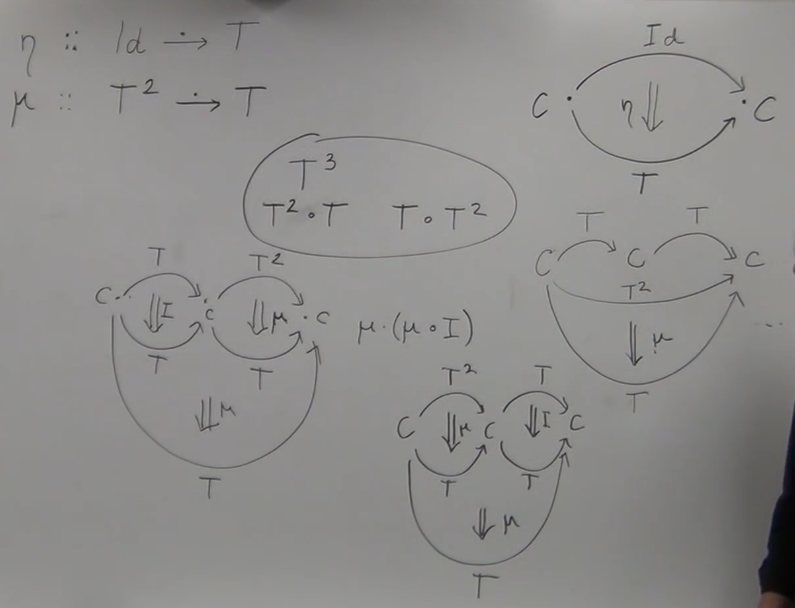
Figure 8: composition of NT -1
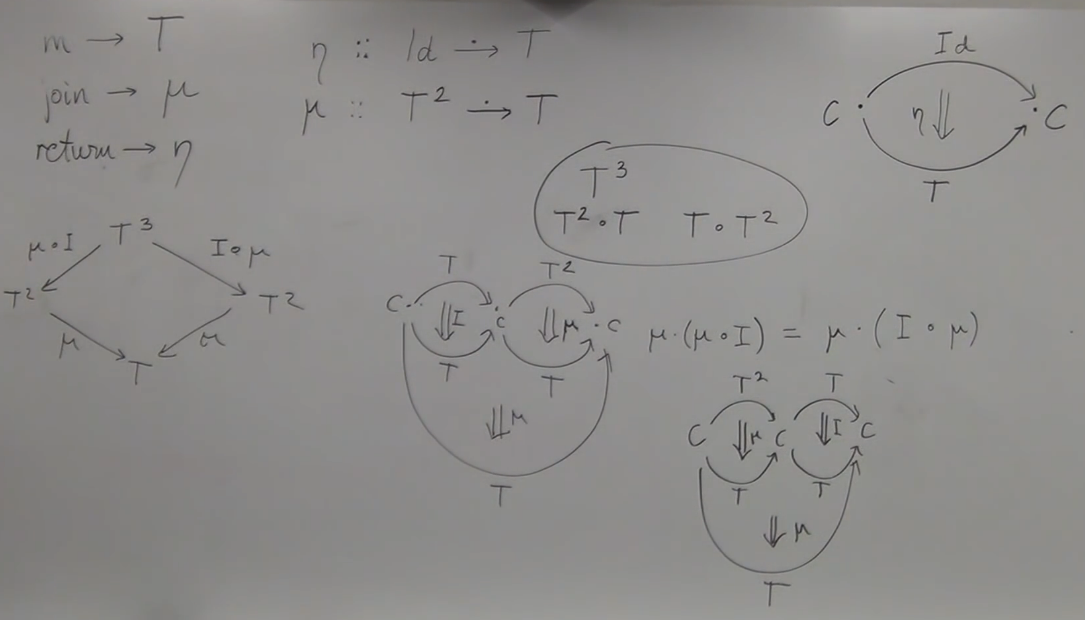
Figure 9: composition of NT -2
μ • (μ ◦ I) = μ • (I ◦ μ)
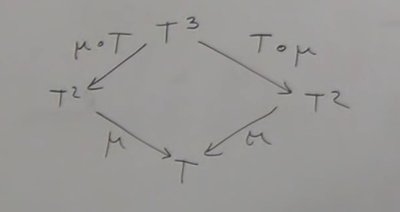
Figure 10: In a Short diagram
proving law 2,3: Monad right/left id by mu and eta
[Notice that] Usually we use T directly short for I. So, if you see
somewhere using this T ◦ μ instead of I ◦ μ, you should know that
they are the same meaning.
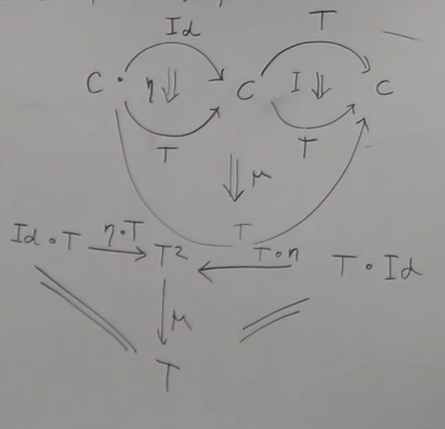
Figure 11: eta is identity (right and left)
this gives us that, eta is Id
we prove these 3 laws of Monad — assoc + r id + l id, in terms of /mu and /eta.
Cat 10.2 Monoid in the category of endofunctors
So, now you can say:
Monad is the monoid in the category of endofunctors
recall all these 3 concept: 1. Monad = T23 - T : a enfofunctor - 2 : eta and mu are Natural trans - eta: Id ->. T - mu : T\^2 ->. T - 3 : laws of Monad: 1. assoc : mu • (mu ◦ I) = mu • (I ◦ mu) 2. L id: Id ◦ T = T 3. R id: T ◦ Id = T 2. monoid - every monoid is a single object category - 2 laws of Monoid: - identity: a append id = a - assoc: a append ( b append c) = (a append b) append c - eg. "List forms a monoid under append with identity empty list" 3. Category of endofunctors - endofunctor: from Category C to C - every objects of Category is a endofunctors - every morphism of Category is a natural transformations
how to get away from set in Monoid — a more general definition of
Monoid
:CUSTOM_ID: how-to-get-away-from-set-in-monoid-a-more-general-definition-of-monoid
lifting the abstraction of set to a category.
mu :: (a, a) -> a / def(int,int):int eta :: () -> a / def(unit):int
mu and eta are morphism of Cartesian product category, input type of mu is product, input type of eta is terminal object.
take Monoid laws into account: assoc laws: mu( mu(x,y), z) = mu( x, mu(y,z)) identity laws: mu( eta(), x) = x mu( x, eta()) = x
you should remember that:
product category has pair as object, has also pair functions as morphism, some like a bifunctor.
Taking a pair type — the product in haskell, is monoidal up to 3 isomorphism: 1. α(can be implemented by case match clause) 2. λ(just name of function,not λ terms in haskell) 3. ρ
Monoidal category is just a straightforward generalization of this.It's a category in which we have categorical product and terminal object. But we can do more, why product, why not coproduct, it could be also a monoidal thing — it was associative up to isomorphism and it had a unit which is a void empty set.
So ,in general we can have a monoidal category and the only requirement for it is that it has a tensor product and identity object. Monoidal category has a bifunctor and this object I — identity object.
So, If we have a monoidal category we have a more general definition of a monoid.
we can define a monoid to be an object of Monoidal category with 2 morphism: * object m in Monoidal category * mu :: m ⊗ m -> m * eta :: I -> m
pair | product | tensor product |
set category | catesian category | monoid category |
everytime lifting abstraction up a little bit, everytime more general.