lec-17 Deep Generative Model
Table of Contents
- 1. Deep Generative Model
- 2. GAN(生成对抗网络)
- 3. Go on GAN
- 4. Improving GAN
- 5. 1) Basic idea of GAN
- 6. 数学解释
- 7. 2) Unified Framework
- 8. 3) WGAN
- 9. Improved version (gradient penalty)
- 10. 5) Energy-based GAN
- 11. Review: Chat-bot
- 12. RL
- 13. SeqGAN
- 14. how to improve seqGAN
1 Deep Generative Model
>>> Richard Feynman ----------------------------------------------------- what i cannot create, i do not understand. 我没法创造的东西,说明我不够理解。 -----------------------------------------------------
让机器自己学习创造
Generative Models 大概的三个方法:
- Pixel RNN
- VAE - Variational Autoencoder
- Generative Adversarial Network
1.1 VAE
1.1.1 普通 autoencoder
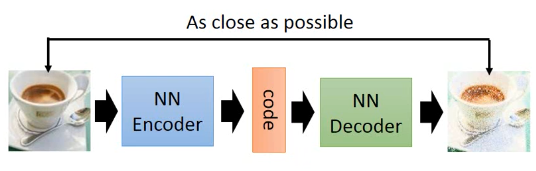 这是训练 autoencoder 的过程
这是训练 autoencoder 的过程
我们希望这个过程中训练出来的 decoder 可以实现随便给一个 code 就能通过 decoder 生成一个图片,这样可以做,但效果不好
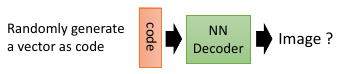
1.1.2 改进 autoencoder — VAE
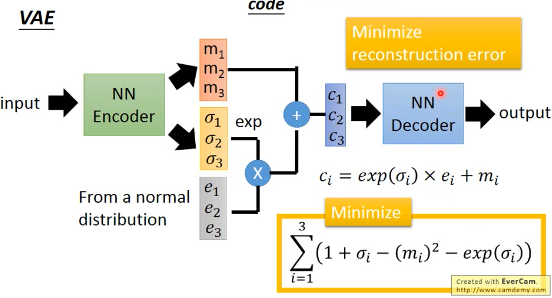 要同时最小化兩個公式【注】ppt 中,下面的公式写错了, 括号里面要加负号
要同时最小化兩個公式【注】ppt 中,下面的公式写错了, 括号里面要加负号

1.1.3 VAE 生成细节控制
我想把宝可梦压缩到 10 维度按照 AVE 的模型训练之后,得到 decoder 我采用类似【生物课】试验的方法:依次固定其中的 8 维度,在另外 2 维度上均匀变化用这样的方法,研究每一个维度上的意义,如果我能把 10 个维度的意义都搞清楚我就可以通过选择不同的 code,来生成不同的宝可梦图片 Pick two dim, and fix the rest eight
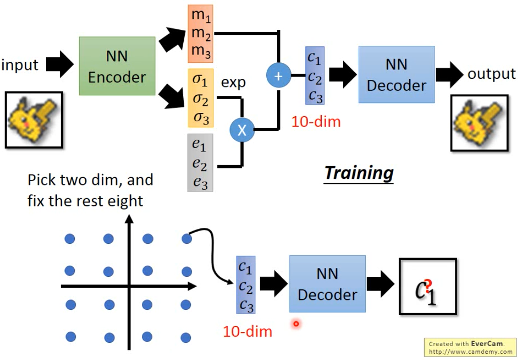
选取其中 2 dim

选取另外的 2 dim

1.1.4 用 VAE 来写诗
因为 sentence 是句子,所以要结合 RNN 来使用
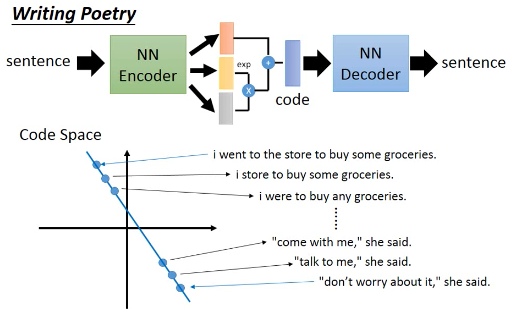
Ref: http://www.wired.co.uk/article/google-artificial-intelligence-poetry Samuel R. Bowman, Luke Vilnis, Oriol Vinyals, Andrew M. Dai, Rafal Jozefowicz, Samy Bengio, Generating Sentences from a Continuous Space, arXiv prepring, 2015
1.2 Why VAE?
1.2.1 Intuitive Reason
假设 code 是一维度的
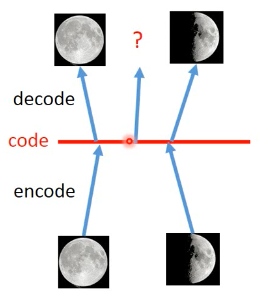
如果我们在已经知道的两张图片对应的 code 点中间做 decoder 能得到在满月和弦月之间的月相么?很难,因为 deep auto-encoder 是非线性的。而我们希望的月相,介于满弦之间是一种线性的映射关系。
AVE 可以做到,AVE 相当于加入了 noise,在加入 noise 之后,原来的一个 code 映射一张图片,变成一个 【code 区间】都会映射同一张图片。所以:
[code 区间 1] ---> 满月 [code 区间 2] ---> 弦月
区间 1 和区间 2 之间的 code 点怎么办呢?
通过 mean square error, 让他最像满月也最像弦月,那他有可能产生介于满弦之间的月相所以,如果用原来的 auto-encoder 你在 code 上 random sample 的点,不像是真实的 image 。但是在 AVE 上,在 code 上 random sampble 得点,有很大可能 reconstruct 回不错的图片。

1.2.2 理性认识
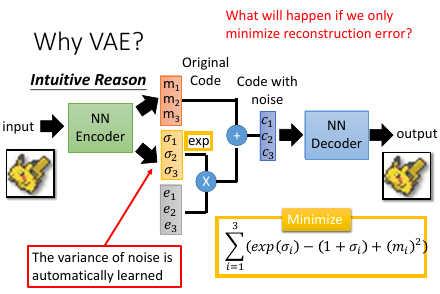
e 是从 normal distribution sample 出来的, variance 本来是固定的 但是乘以不同的 σ 之后呢, variance 就有所改变. variance 决定了 noise 的大小。而 variance(亦即σ)是从 encoder 产生的。也就是说这个 NN 会自动 learn 出这个 variance 应该是多大。 m 是原始 code c 是加上 noise 之后的 code σ 代表 noise 的 variance,取 exp 确保他是一个正值,确保他可以被看成 variance.
但只有这些是不够的,因为这个 variance 是 NN 自己学的,要最小化 reconstruction error, NN 一定会让这个 variance=0 .就变回最基本的 auto-encoder 了
所以要对 variance 加一个限制,不让他变的太小。
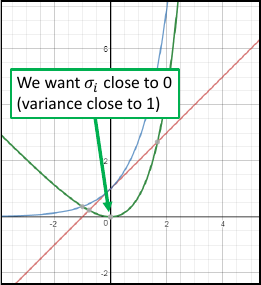 蓝色线是 exp(σ)
红色线是 1+σ两者相减是绿色线,这个绿色函数最小值是 σ=0 那一点也就是说 loss-fn 取最小值时,σ = 0
当 σ=0 时, variance = exp(σ) = 1
所以 variance 最小为 1.
也就是说 loss-fn 取最小值时, variance = 1
也就是通过修改 loss-fn 就使得 variance 不会太小
蓝色线是 exp(σ)
红色线是 1+σ两者相减是绿色线,这个绿色函数最小值是 σ=0 那一点也就是说 loss-fn 取最小值时,σ = 0
当 σ=0 时, variance = exp(σ) = 1
所以 variance 最小为 1.
也就是说 loss-fn 取最小值时, variance = 1
也就是通过修改 loss-fn 就使得 variance 不会太小
 这里的 m2 就是 L2-regular, 用来防止训练出的 m 太稀疏
这里的 m2 就是 L2-regular, 用来防止训练出的 m 太稀疏
>>> loss-fn ---------------------------------------------------- loss-fn 就像是钱坤袋,你堆模型的任何要求,都可以把這些要求转换 成数学语言,然后丢进钱坤袋中,模型就像电脑一样,会给你执行出你要 的结果。 果真,算法就是数学,这里的钱坤袋就是算法,而模型就是电脑。 ----------------------------------------------------
1.3 正式的数学解释
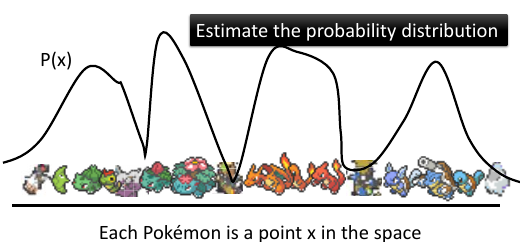
目标: 产生宝可梦的图片已知: 一堆高维空间中的点
 参考概率视角下的分类问题参考 Distributed Representation
某一组样本点就是由一个高维空间中的概率分布产生的,只要获得了这个概率分布,我们就可以自己生成样本点。同样的道理,如果我们能找到这堆宝可梦图片(图片也是一种像素表示的高维空间样本点)的概率分布 P(x),我们就能自己生成图片。
参考概率视角下的分类问题参考 Distributed Representation
某一组样本点就是由一个高维空间中的概率分布产生的,只要获得了这个概率分布,我们就可以自己生成样本点。同样的道理,如果我们能找到这堆宝可梦图片(图片也是一种像素表示的高维空间样本点)的概率分布 P(x),我们就能自己生成图片。
P(某个图片) 值较高 ---> 图片出现概率高 ---> 像是人设计的图片 ---> 图片正常 P(某个图片) 值较高 ---> 图片出现概率低 ---> 不是人设计的图片 ---> 图片诡异
1.3.1 Gaussian Mixture Model
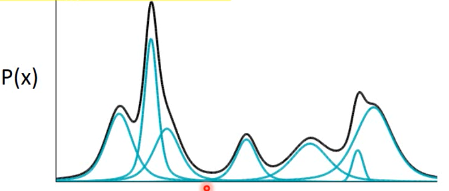
比如我们有一个很复杂的分布(黑色)。可以把他理解成 很多个高斯(绿色)用不同的 weight 合成的 只要高斯分布足够多,就可以产生任何复杂的分布。
>>> 混合高斯模型公式
-----------------------------------------------------
P(x) = P(x ⋂ m1) + P(x ⋂ m3) + P(x ⋂ m3) ...
= P(m1)P(x|m1) + P(m1)P(x|m1) + P(m1)P(x|m1) ...
= ΣP(mi)P(x|mi)
-----------------------------------------------------
+-------------------+--------------------+
| m4 +----------+----------+ m1 |
| | | | |
| | x ⋂ m1 | .... | |
+--------+----------+----------+---------+
| m5 | | | m2 |
| | | | |
| | | | |
+--------+----------+----------+---------+
| m6 | | | m3 |
| | | | |
| +----------+----------+ |
+-------------------+--------------------+
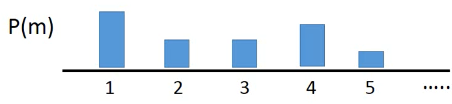
怎么 sample data 呢?
- 先选择高斯编号
- 再从那个高斯中 sample
跟基本混合模型是一样的,一旦决定使用哪一个高斯,剩下的事情就和混合模型没关系了,只跟这个被选中的高斯由关系。
 m 表示第幾個高斯
x|m 表示从第 m 个高斯中抽取样本
m 表示第幾個高斯
x|m 表示从第 m 个高斯中抽取样本
混合高斯分布,还有其他很多东西要决定: mixture 的数目如果已经决定了这个数目,那么 input: dataset outpu: 每个小高斯的 weight,μ,Σ这个可以用 EM Algorighm 来解,也有特定的程序包可以做, 总之很简单。
这样之后每一个样本点的产生概率,都可以用 数个小高斯 来表示,这个很像分类问题中的 Distributed Representation: Distributed representation is better than cluster
eg. 小志是这样的英雄 | 强化系 | 0.70 | | 放出系 | 0.25 | | 变化系 | 0.05 | | 操作系 | 0.00 | | 特质系 | 0.00 |
>>> VAE 的本质 ---------------------------------------------------------------------- *所以 VAE 就是 Gaussian Mixture Model 的 distributed representation 版本* ----------------------------------------------------------------------
1.3.2 加强版高斯混合模型
上面的高斯混合模型,是使用【有限个】高斯来合成一个复杂的分布: P(x) = ΣP(m)P(x|m) P(m) 相当于第 m 个高斯的权重(选择第 m 个高斯的概率)
>>> 无数个高斯
----------------------------------------------------------------------
1) 先选择高斯编号:m
2) 再从那个高斯中 sample:x
----> 1) 从 Normal 分布中 sample 出一个实数(编号):z
----> 2) 根据这个实数的某个 func 产生某个高斯分布,从这个高斯分布中 sample:x
基础版的高斯混合模型是 [指定幾個高斯]
而加强版的高斯混合模型是 [利用 normal 分布来生成高斯]
高斯.mean = μ(z)
高斯.var = σ(z)
两者的本质是一样的: 基本混合模型 m 决定了 高斯的 mean 和 variance
加强混合模型 z 决定了 高斯的 mean 和 variance
----------------------------------------------------------------------
z 的每一个 dimension 都代表了他要 sambple 的那个东西的某种特质

1.3.3 利用神经网络
现在怎么找到这两个函数呢?
 也就是输入 z-space 一个点,输出 x-space 的 mean 和 variance 是多少跟基本混合模型是一样的,一旦决定使用哪一个高斯,剩下的事情就和混合模型没关系了,只跟这个被选中的高斯由关系。这里也是一样,z 一旦被选出来,那根据高斯.mean = μ(z)
高斯.var = σ(z)
这个高斯也就确定了,那么 P(x) 也就确定了
也就是输入 z-space 一个点,输出 x-space 的 mean 和 variance 是多少跟基本混合模型是一样的,一旦决定使用哪一个高斯,剩下的事情就和混合模型没关系了,只跟这个被选中的高斯由关系。这里也是一样,z 一旦被选出来,那根据高斯.mean = μ(z)
高斯.var = σ(z)
这个高斯也就确定了,那么 P(x) 也就确定了
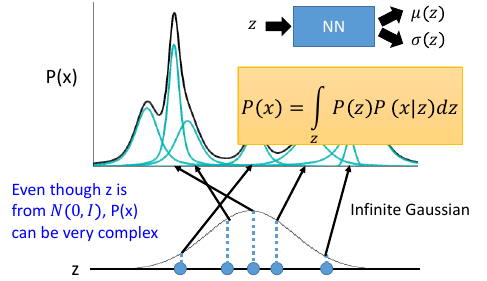 那 z 能否不用 normal distribution,能不能让 z 是更复杂的分布?完全可以,z 可以是任何分布,但是由于 NN 是很强的,它可以实现任何函数所以 z 只用 normal distribution 就足够了。
那 z 能否不用 normal distribution,能不能让 z 是更复杂的分布?完全可以,z 可以是任何分布,但是由于 NN 是很强的,它可以实现任何函数所以 z 只用 normal distribution 就足够了。
1.3.4 Maximizing Likelihood
如何利用神经网络找到这兩個函数呢?

>>> 基本混合模型与加强混合模型 --------------------------------------------------------------- P(x) = ΣP(mi)P(x|mi) - 先选 m, 然后找到 m 对应的分布,产生 x 点的概率就是 m 对应的分布产生的 - P(mi), (μi,σi) , P(x|(μi,σi)) P(x) = ∫P(z)P(x|z)dz - 先生成 z, 然后根据 z 生成某个分布,产生 x 点的概率就是 m 对应的分布产生的 - P(z) ,(μ(z),σ(z)) ,P(x|(μ(z),σ(z))) ---------------------------------------------------------------
注意 这里的 L=ΣlogP(x) 是 'likelihood',不是 loss-fn 这里的 x 就是我们手上已经有的宝可梦的图片,我们要通过最大化 likelihood 来让 NN 学到 μ(z) σ(z) [注意,这里学到这两个函数的意思就是,input-layer 是 z,output 就是两个与 z 同维度的向量,其中一个向量是 μ向量,一个是 σ向量]
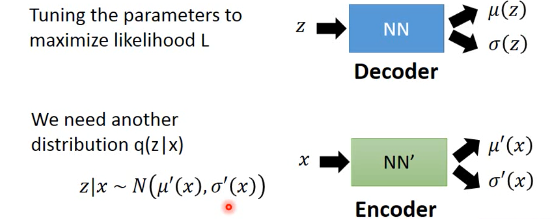 其实从 z 得到 x-space 的 mean 和 variance 就是 Decoder
从 x 得到 z-space 的 mean 和 variance 就是 Encoder
其实从 z 得到 x-space 的 mean 和 variance 就是 Decoder
从 x 得到 z-space 的 mean 和 variance 就是 Encoder

[qqq] ------------------------------------------------------ 注意 ∫q(z|x)dz = 1 . why? ∫q(z|Ω)dz = 1 条件概率中的 'x' 'Ω'就相当于‘国界’,表示我仅仅考虑这个范围内的 z. 所以 logP(x) = ∫q(z|x)logP(x)dz 是一个恒等式。 对于任何 q(z|x) 都适用,同时也说明一个重要的事实,Likelyhood 的取值 跟 q(z|x) 一點关系都没有。 这个重要的事实 下面会起到决定性的优化作用。 ------------------------------------------------------
1.3.5 KL divergence
KL divergence 用来表示两个分布的【相似性】,他是一个【距离】的概念,衡量了两个分布的【距离】
>>> 相似性 similarity
-----------------------------------------------------
相似性到目前为止:
: 两个向量是否相似:inner-product
: 两个分布是否相似:cross entropy
: 自己跟自己是否相似:how concentrate(cross entropy)
: ==> 两个分布的距离是否相近:KL divergence(公式与 cross entropy 有点像)
-----------------------------------------------------
距离永远 >= 0
KL 永远 >= 0
KL 越大代表这两个分布越不像;
KL =0, 如果这亮哥分布完全一样;
由于 KL 永远大于零
所以 ∫q(z|x)log(P(z,x)/q(z|x)) 就是 likelihood 的 lower-bound
在这个公式中 P(z) 是已只知的
Lb --- lower bound of Likelihood
知道這些,仍然没有任何作用,有可能我最大化 Lb 的时候 Likelyhood 还在下降
因为毕竟仅仅是个 [下界] 而已。
1.3.6 引入 q(z|x)
引入 q(z|x) 恰好可以解决这个问题:因为 q(z|x) 是与 Likelyhood 没有任何关系的,不论 q(z|x) 是多少,Likelyhood 都不会受影响(logP(x) = ∫q(z|x)logP(x)dz 是一个恒等式)但是 q(z|x) 却可以影响 Likelyhood 的下界:Lb,这无形中,也就影响了 KL 的大小。当你 maximize q(z|x) 的时候,就是在 maximize Lb, 就是在 minimize KL. 然后 Lb 会与 Likelyhood 越来越接近。
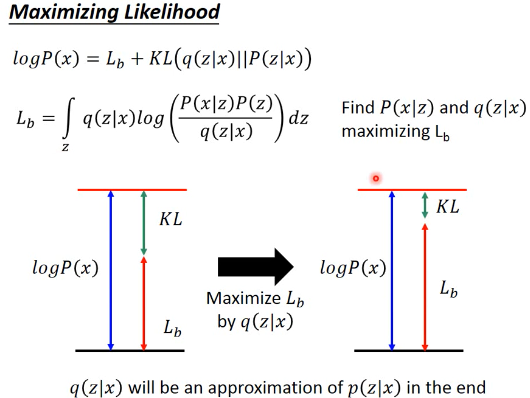
Likelyhood = Lb + KL Likelyhood 只与 P(x|z) 正相关 Lb 与 P(x|z) 和 q(z|x) 正相关 固定 P(x|z) 时,Likelyhood 不变 固定 P(x|z) 同时最大化 q(x|z) ---> Likelyhood 不变,最大化 Lb ---> 也就是在最小化 KL ---> 随着 KL 越来越小,KL 是衡量 q(z|x) 和 P(z|x) 分布之间的距离,所以两个分布会越来越近 ---> 而且,随着 KL 越来越小 , Lb = Likelyhood ---> keep KL ~~ 0 , 提升 Lb 就是在提升 Likelyhood
所以现在的方法就变成:Find P(x|z) and q(z|x) maximizing Lb 下面就是对 Lb 进行化简
 化简之后,可以得到另一个 KL: KL(P(z) || q(z|x)) = -KL(q(z|x) || P(z)),
而之前讲过:
Decoder : P(z|x) : P 就是 Decoder
Encoder : q(x|z) : q 就是 Encoder
所以最小化 KL(q(z|x) || P(z)) 就是最大化 Lb
最小化 KL(q(z|x) || P(z)) 也就是调整 Encoder 让他产生的 distribution
与 一个 normal distribution:P(z),越接近越好,而 P(z) 是已知的他与
化简之后,可以得到另一个 KL: KL(P(z) || q(z|x)) = -KL(q(z|x) || P(z)),
而之前讲过:
Decoder : P(z|x) : P 就是 Decoder
Encoder : q(x|z) : q 就是 Encoder
所以最小化 KL(q(z|x) || P(z)) 就是最大化 Lb
最小化 KL(q(z|x) || P(z)) 也就是调整 Encoder 让他产生的 distribution
与 一个 normal distribution:P(z),越接近越好,而 P(z) 是已知的他与
 的作用是一致的 Minimize KL(q(z|x) || P(z)) = Minimize Σ(exp(σ)-(1+σ)+m2)
的作用是一致的 Minimize KL(q(z|x) || P(z)) = Minimize Σ(exp(σ)-(1+σ)+m2)
1.3.7 结合这个,再回头看整体公式


视角一: -------------------------------------------------------------------- 我们想生成某种满弦之间的月相,原始 auto-encoder 由于非线性的关系,是搞不定的。 所以我们引入 AVE,他为什么 work 呢?因为他加入了 noise,让满弦 with noise 同时去‘夹’这个图片的生成。这是产生 AVE 的网络结构的原因,但是如果仅仅去最小化 reconstruction error 来优化参数,这个网络结构会直接把 noise 的 variance 取零。 所以, 加入一些限制来让 noise 的 variance 最小为 1. 视角二: -------------------------------------------------------------------- 这之后通过对生成模型的交叉理解,知道我们要找的其实就是一个可以产生这样样本月相的 概率分布。只不过这个概率分布可能很复杂,是由须多小的高斯分布混合而成---高斯混合模型。 通过对高斯混合模型的理解,得到 P(x|z) 就是 Decoder,q(z|e) 就是 Encoder 的结论。 利用对 q(z|e)引入,固定 likelyhood 提升 Lb 的方法,使得 Lb~~Likelyhood.问题 变成 只要 q(z|e) 能逼近 P(z) 就能最大化 Lb,也就可以最大化 Likeylyhood. 视角一 + 视角二: -------------------------------------------------------------------- 依据 P(x|z) 就是 Decoder,q(z|e) 就是 Encoder 这个结论,视角二,也可以被归结到 视角一 提供的 NN 结构中解决。 logP(x) = ∫q(z|x)logP(x)dz 把 q(z|x) 看成权重,把 log(P(x|z))看成某个变量 这个式子整体就是一个 权重版平均(期望),只不过权重不是固定的,而是某个分布中 sample 出来的。
logP(x) = ∫q(z|x)logP(x)dz
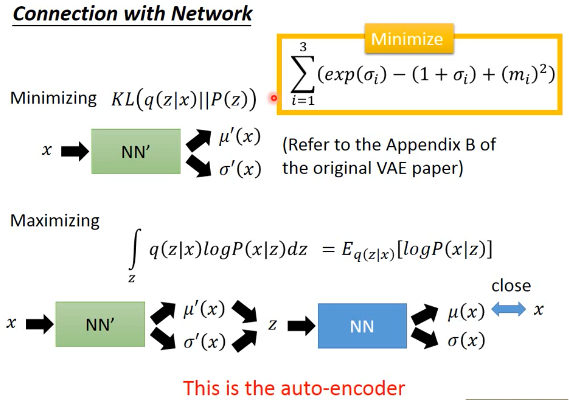 问题最后变成:
input 一个 x 产生两个 vector,共同组成一个分布,从分布中 sample 一个 z
再由这个 z 产生另外两个 vector,组成另一个分布,使得代表 mean 的那个 vector
跟原来的 x 越接近越好。为甚么?因为你最后 z 产生的分布就是某个简单的高斯分布,而 x 要想最大几率,就是让这个高斯分布的 mean 接近 x.越接近,x 产生的概率越大。
问题最后变成:
input 一个 x 产生两个 vector,共同组成一个分布,从分布中 sample 一个 z
再由这个 z 产生另外两个 vector,组成另一个分布,使得代表 mean 的那个 vector
跟原来的 x 越接近越好。为甚么?因为你最后 z 产生的分布就是某个简单的高斯分布,而 x 要想最大几率,就是让这个高斯分布的 mean 接近 x.越接近,x 产生的概率越大。
又是从 x -> x,所以整体就是一个 auto-encoder
1.3.8 Conditional VAE
让 VAE 可以生成‘风格相似’的图片(比如手写数字)给 VAE 看一个 digit,他会把这个手写数字的特性抽取出来(比如笔画粗细等地概念)接下来,你在丢进 encoder 的时候 , 你一方面给他一个关于这个手写数字的特性的一个分布, 另外一方面告诉他这是什么数字, 你就可以根据这一个 digit,生成跟他‘风格相似’的 digit [这个跟 stanford cs20si lec-6 讲的东西很像:内容和风格]
1.3.9 Problems of VAE
VAE 的一个最大的问题就是,他从来没有学习如何产生【看起来像人做的】图片。他学的仅仅是,如何产生一个跟 smaple 中某张 or 某幾張越接近越好的图片。对 VAE 来说,他对下面两张图片的评价是一样的。但是很明显,人类认为左边的更好,VAE 就只知道【算量】---太理性,而人还知道【算性】---理性+感性
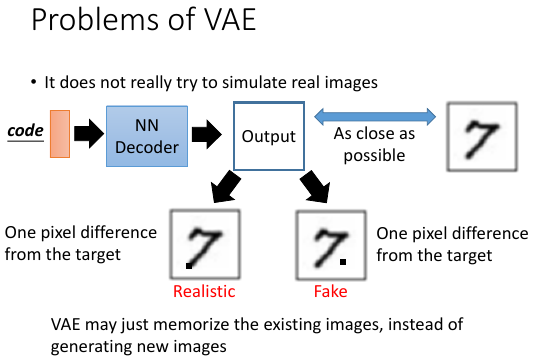
2 GAN(生成对抗网络)
>>> 李红义老师之前的将可录像,关于 RBM 和 Gibbs Sampling
Restricted Boltzmann Machine: http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/RBM (v2).ecm.mp4/index.html Gibbs Sampling: http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/MRF (v2).ecm.mp4/index.html
>>> Lan Goodfellow tutorial about GAN (李红义老师极力推荐)
• Author: Ian Goodfellow • Paper: https://arxiv.org/abs/1701.00160 • Video: https://channel9.msdn.com/Events/Neural- Information-Processing-Systems- Conference/Neural-Information-Processing- Systems-Conference-NIPS-2016/Generative- Adversarial-Networks • You can find tips for training GAN here: https://github.com/soumith/ganhacks
2014 年才出来的技术 Ian J. Good fellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio, Generative Adversarial Networks, arXiv preprint 2014
2.1 拟态的演化
枯叶蝶的进化过程
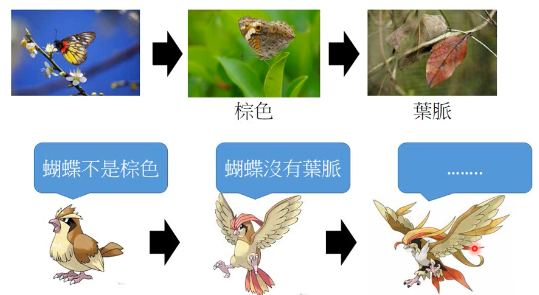
The evolution of generation
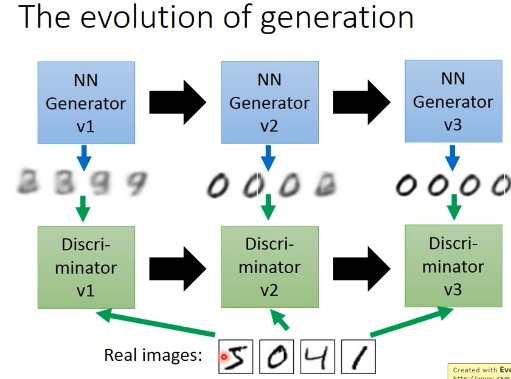 鉴别器会根据 本代生成器产生的图片 和 样本中的图片,来调整自己的参数,保证自己可以查出 生成器图片的瑕疵。
鉴别器会根据 本代生成器产生的图片 和 样本中的图片,来调整自己的参数,保证自己可以查出 生成器图片的瑕疵。
生成器会根据 上一代生成器 和 上一代鉴别器 做改进再生成图片,保证自己的图片可以骗过 上一代鉴别器。
注意生成器从来没有看过样本数据,第一代生成器基本是 random 生成。他的毕生目标只是为了骗过鉴别器。所以它可以生成 样本中没有的图片。这是 GAN 得以 work 的根本。
2.2 鉴别器
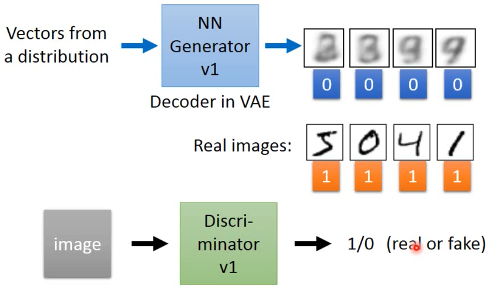
鉴别器和生成器都是 NN, 生成器特别像 VAE,他的输入也是某个分布中 sample 出来的 code
然后经过生成器生成图片。
鉴别器就是把 生成的图片都 label 为 0.
把 样本的图片都 label 为 1.
他们共同组成了 一个 labelled dataset 成为训练集。
接下来就是一个 binary classification 问题,训练好鉴别器的 NN 之后,输入一个新的图片
输出这个图片的标签是 0 or 1.
2.3 生成器
生成器怎么更新换代呢?主要的工作就是【成功欺骗】上代鉴别器把生成器与鉴别器连在一起形成一个 NN,目标是整个 NN 的输出结果尽量接近 1 但是我们只要 生成器做 update, 保持鉴别器的参数不变 Fix the discriminator
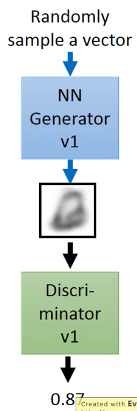
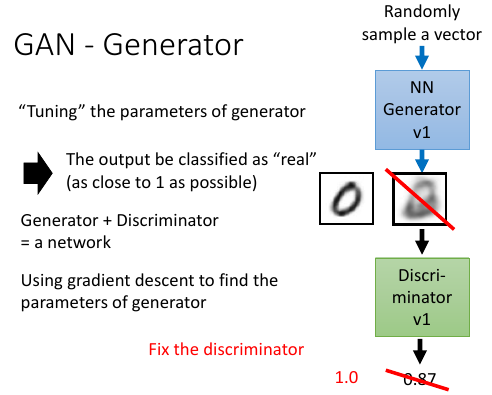
>>> loss-fn -------------------------------------- 这里对 NN 的额外要求并没有被做进 loss-fn 中 而是 Fix 住 NN 的一部分来实现 这里提供了一种思路: *神经网络可以只更新一部分.* --------------------------------------
2.4 GAN - toy example
z-space 就是 decoder 的输入, 一个 hiden variable 生成器的目标就是骗过鉴别器,所以他重新调整之后会朝着左边移动向着鉴别器输出的分类概率值更大的方向移动。
Demo: http://cs.stanford.edu/people/karpathy/gan/
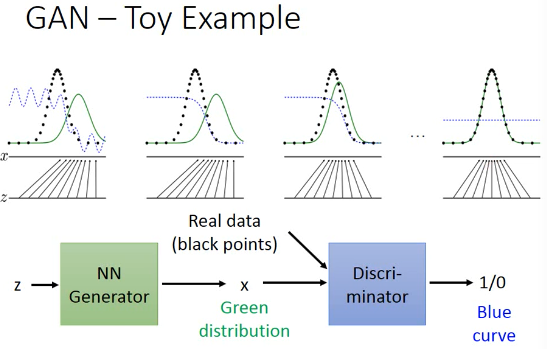
>>> 如何让某种分布向某个方向移动? -------------------------------------- 这里的 GAN 模型很好的给出了一种,让某种分布自动 的变成另一种分布的方法。 --------------------------------------
但是有两个问题,至今无解:
- 不知道新的生成器到底会向那个方向移动多少,有可能一下就移过头了,所以需要【非常小心的调整】 参数。
- 不知道鉴别器是否是正确的,如果鉴别器显的很强能一直找到瑕疵,这不代表鉴别器很好,有可能是生成器太弱了,反之也是。
所以真正在做 GAN 的时候,你会一直不断的让生成器生成一些图片看看是否比以前更好。 GAN 非常难以训练但是他就像大绝招,一旦能熟练的使用,你就牛逼了。彻底的牛逼了。
2.5 In practical
• GANs are difficult to optimize. • No explicit signal about how good the generator is • In standard NNs, we monitor loss • In GANs, we have to keep “well-matched in a contest” • When discriminator fails, it does not guarantee that generator generates realistic images • Just because discriminator is stupid • Sometimes generator find a specific example that can fail the discriminator • Making discriminator more robust may be helpful.
3 Go on GAN
3.1 review Auto-encoder and VAE
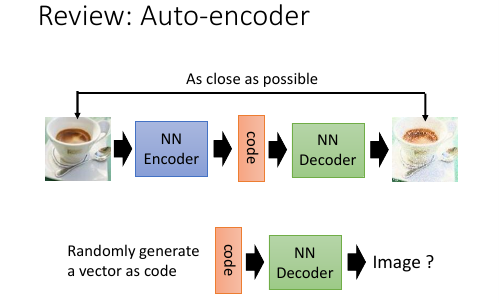
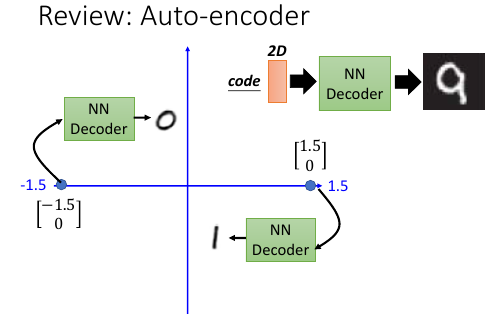

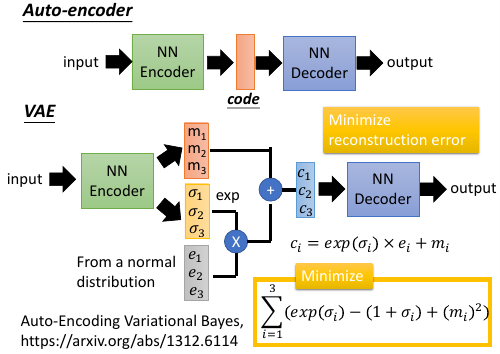
Auto-Encoding Variational Bayes, https://arxiv.org/abs/1312.6114
Problems of VAE 他没有真的【学会人的‘观点’】:

新的生成模型:与天敌竞争
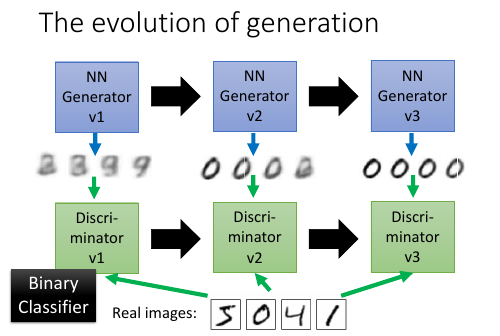
3.2 GAN - Discriminator
Discriminator 鉴别器的本质就是一个 贰元分类器
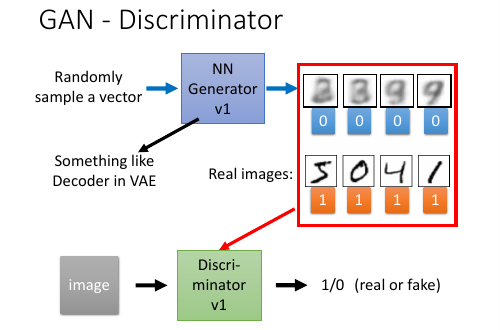
3.3 GAN - Generator
与 VAE decoder 部分结构一模一样,只是训练方法不同:生成器和鉴别器接起来,但是 fix 住鉴别器的参数,只用 GD 更新生成器的参数,(中间要有一个 layer 跟图片的大小是一样的)表示生成器生成的图片。

3.4 GAN 二次元人物头像炼成
Source of images: https://zhuanlan.zhihu.com/p/24767059 DCGAN: https://github.com/carpedm20/DCGAN-tensorflow DCGAN 跟 GAN 都是一样的,不一样的地方是:Layer 的架构都是 CNN 的。 DCGAN = Deep Convolutional GAN





4 Improving GAN
4.1 Outline
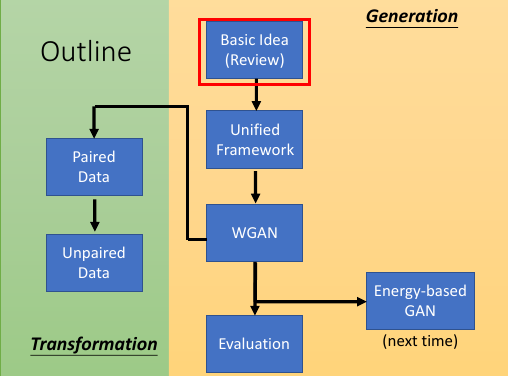
- Generation
- Basic Idea
- Unified Framework
- WGAN
- Evalution
- Energy-based GAN
- Transformation
- Paired Data
- Unpaied Data
5 1) Basic idea of GAN
5.1 Maximum Likelihood Estimation
生成模型都离不开概率分布,每一个分布就像一个【模版】,你可以根据模版生成无限的图片目标就是找一个 distribution.
Pdata(x) 就是我们目标分布,data 每个样本就是一个图片,把所有像素连接起来形成一个长向量。
但是目标分布就是 target-fn 一样我们不知道,我们需要找到一个 PG(x;θ) θ是我们可以操控的参数。他是最有可能产生出样本集中数据的一个目标分布的近似分布。
PG(x;θ) 可以是高斯混合,也可以是 NN,我们要的是 NN,但可以通过高斯混合来理解:我要找的就是诸多高斯的 means, variances 和 高斯的 weights.

>步骤< Maximum Likelihood 做 log 转换
 这里是用 sample 的方式来计算,那是因为没有办法直接做积分来计算,所以是用
sample 的方式计算,来逼近目标分布:Pdata(x)。
这里是用 sample 的方式来计算,那是因为没有办法直接做积分来计算,所以是用
sample 的方式计算,来逼近目标分布:Pdata(x)。
x~Pdata 表示从 Pdata 这个目标分布中 sample x. Ex~pdata[logPG(x;θ)] = ∫Pdata(x)logPG(x;θ)dx
>>> 一句话理解最大似然法: ------------------------------------------------------------------- *从 pdata 分布中取样的样本,在 PG(x;θ) 中出现的概率的期望(加权平均值)越大越好* -------------------------------------------------------------------
'- ∫Pdata(x)logPdata(x)dx' 这一项并不会影响求最大值,但是加上之后,整个式子可以化简成:KL divergence KL divergence 的作用就是衡量 两个分布的相似性,衡量两个分布的距离因为是一个距离的概念,所以 KL divergence 始终是正的。
>步骤< 问题就从 Maximum Likelihood —> Minimize KL divergence
高斯混合太不 generalize 了,他是有限制的,他没法 model 不同的 Pdata 我们可以有一个非常 generalize 非常复杂的 PG
5.2 Now PG is a NN
 θ 就是 NN 的参数。
z 即使是 normal distribution, 而通过一个 NN,完全可以变成一个比高斯分布还要复杂的分布。因为 NN 是十分 power 十分 generalized
θ 就是 NN 的参数。
z 即使是 normal distribution, 而通过一个 NN,完全可以变成一个比高斯分布还要复杂的分布。因为 NN 是十分 power 十分 generalized
PG(x;θ) -—> PG(x) PG(x) 应该是一个什么样的表达式呢?如上图的表达式,有点类似上页 ppt 的高斯混合模型的表达式:注意 I[G(z)=x] 表示: 如果[]内的表达式为真,整个式子返回 1;否则返回 0.
表达式的意义是:
- 从 NN 中输出 x 的几率是多少呢?PG(x)
- 积分所有可能的 z,每个 z 产生的几率不一样。Pprior(z)
- 每个 z 通过 NN 是否恰好能产生 x。I[G(z)=x]
但写成这样,没法算 Likelihood, 因为 G 可能很复杂,算出 PG(x) 都未必能够。没法算 Likelihood ,也就没法用 KL divergence 下面怎么办呢?
>>>>>>>>>>>>>>> GAN 登场,代替 MME+KL <<<<<<<<<<<<<<<
5.3 GAN 救场
 鉴别器可以间接起到 KL divergence 的功能。
鉴别器可以间接起到 KL divergence 的功能。
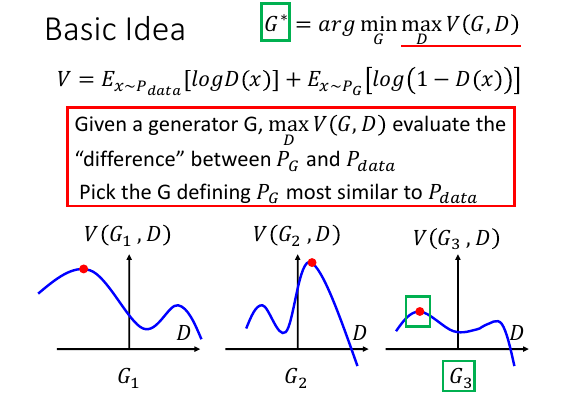 假设世界上只有 3 种生成器:G1,G2,G3
在 V(G,D) 函数的图像中可以看到,如果我定住 G,改变 D 就可以产生不同的数值。
假设世界上只有 3 种生成器:G1,G2,G3
在 V(G,D) 函数的图像中可以看到,如果我定住 G,改变 D 就可以产生不同的数值。
>>> 简单理解 arg min max
-------------------------------------------------------------------------------
G* = argmin_G max_D V(G,D)
拆成两个表达式:
1) D* = arg max_D V(G,D)
2) G* = arg min_G V
........................
1) D* = arg max_D V(G,D)
max_D V(G,D) 这个内层的表达式的意思就是,G 已经给定了,让你找到一个 D 使 V 最大。
注意函数图像,是固定 Gi 下的 V-D 图像,纵轴 V, 横轴 D.
PPT 中函数图像上 三个红点的数值的纵轴 就是这个内层表达式的结果,
三个红点的数值的横轴 就是附属结果 D
假设结果是:V = [(G1,3), (G2,5), (G3,2)],
注意这个结果,这样方便下一步讨论。
*这一步得到的结果是无限多个这样的 V 值,每个 V 值都对应一个 Gi*
*然后从中多 V 值中找到最小的哪个 V 值,及其对应的 G*
2) G* = arg min_G V
min_G V 这个表达式的意思就是,找到一个能让 D* 最小的 G
整个表达式现在变成:
V = [(G1,3), (G2,5), (G3,2)]
G* = argmin_G[(G1,3), (G2,5), (G3,2)]
= G3
很明显能让 V 取最小值的是 G3.
-------------------------------------------------------------------------------
然后来看这个 V, 先别想为甚么是这个表达式,先看如果固定住函数 G, 那么 Pdata 和 PG 就是两个固定(但未知)的分布,V = xxx + xxx Ex~Pdata[logD(x)] 就可以理解为 从 Pdata 中 sample 一个 x,恰好被 D(x) 认为是 人画的概率 Ex~PG[log(1-D(x))] 就可以理解为 从 PG 中 sample 一个 x,恰好被 D(x) 认为是非人画的概率
两者的差距
/--------------------^--------------\
PG 非人画概率 Pdata 人画概率
/<-------------------.-------------->/
------------------------+-------------------------->
非人画 人画
从图中可以看出,只有 MaxVi 才能衡量出 PGi 和 Pdata 的真实差距(difference)然后从众多眾多真实差距(MaxVi) 中找到一个最小的真实差距,其对应的 Gi 和 Pdata 真实差距最小
6 数学解释
6.1 找到 D*
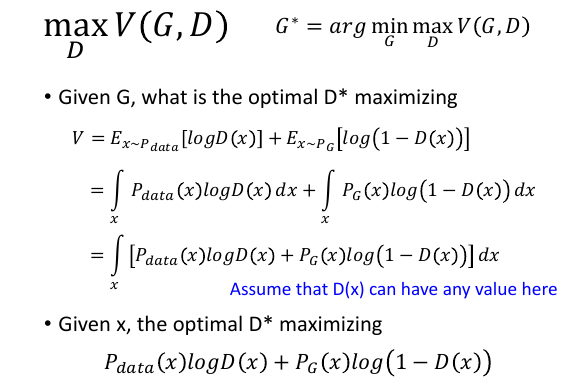

因为求出最好的 D(x) 应该是 0~1 之间,所以在设计 鉴别器 NN 的时候,输出神经元的激活函数应该设置成 sigmoid,这样才能输出一个 0~1 之间的值。
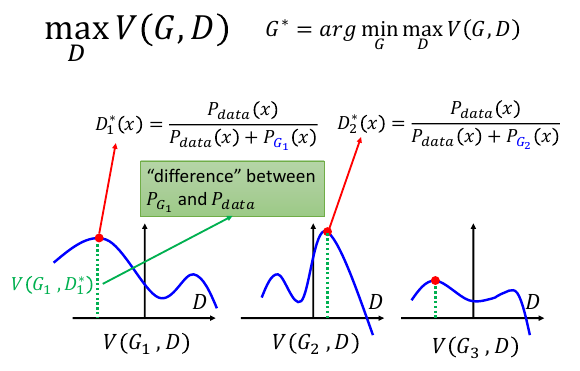 每个 Gi 都对应无限多个 D, 找到那个等于 Pdata/(Pdata + PGi) 的 D, 这个 D 对应的 V 就是
maxVi, 也就是 Gi 与 Pdata 之间的真实差距。
每个 Gi 都对应无限多个 D, 找到那个等于 Pdata/(Pdata + PGi) 的 D, 这个 D 对应的 V 就是
maxVi, 也就是 Gi 与 Pdata 之间的真实差距。
6.2 发现差异度量 Jensen-Shannon divergence
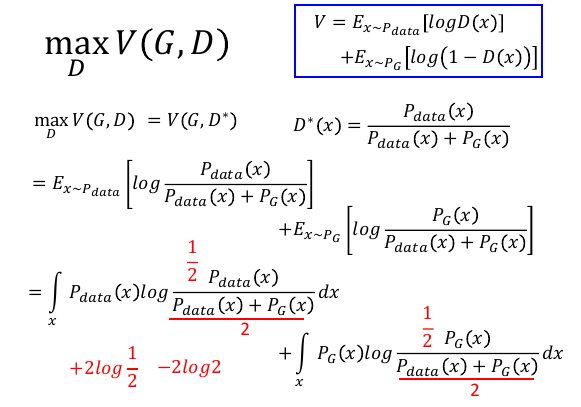 PPT 中是分子分母同除以 1/2
PPT 中是分子分母同除以 1/2
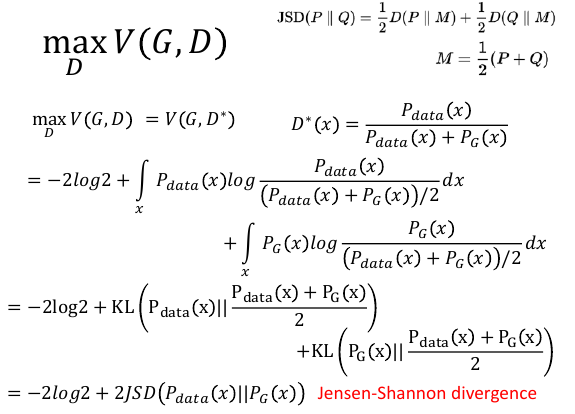 JS divergence 是各自与平均的 divergence 之和。
KL divergence 是非对称的,而 JS divergence 是对称的对称是指:JS(A||B) = JS(B||A)
JS divergence 是各自与平均的 divergence 之和。
KL divergence 是非对称的,而 JS divergence 是对称的对称是指:JS(A||B) = JS(B||A)
KL 就是衡量两个分布的差距,可见 JS 也是一种分布之间差距的度量。所以这个 maxD V(G,D) 确实在衡量 PG 和 Pdata 的某种差距
这里可以定义不同的 V, 那么就会有不同的 divergence JSD <—> V = Ex~Pdata[logD(x)] + Ex~PG[log(1-D(x))]
6.3 找到 G
 JSD(A||A) = 0
JSD(A||A 反) = log2
A||A 反 表示两者完全不同的情况下 JSD = log2
很明显,如果想找到一个 Gi 与 Pdata 真实差距最小,那么就让 PGi(x) = Pdata(x)
这是最理想的。
JSD(A||A) = 0
JSD(A||A 反) = log2
A||A 反 表示两者完全不同的情况下 JSD = log2
很明显,如果想找到一个 Gi 与 Pdata 真实差距最小,那么就让 PGi(x) = Pdata(x)
这是最理想的。
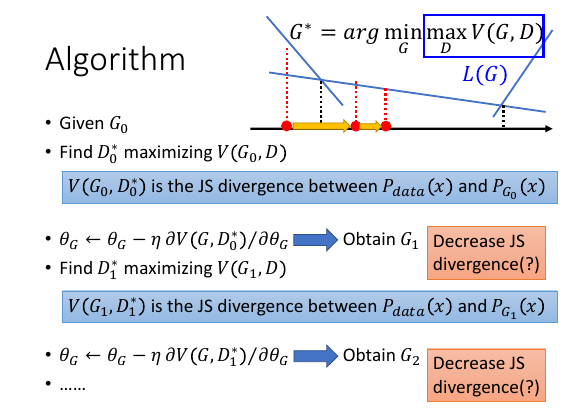
>>> 总结 GAN 基本过程 G 相当于一个关于 V-D 的函数,D 相当于一个数值
loop1: 首先指定一个函数 G0, 然后找到这个 G0 的最大值点(V0,D0),V0 ∝ JS0 然后根据 D0 找到众函数中对应 V 最小的那个,标示其为 G1
loop2: 在 G1 这个函数中找到最大值点(V1,D1),V1 ∝ JS1 然后根据 D1 找到众函数中对应 V 最小的那个,标示其为 G2 …. —>根据一个函数找到最大点,根据这个点找最小函数–>–\ \____________________________________________
6.4 算法
>>> 总结 GAN 基本过程
G 相当于一个关于 V-D 的函数,D 相当于一个数值
loop1:
首先指定一个函数 G0, 然后找到这个 G0 的最大值点(V0,D0),V0 ∝ JS0
然后根据 D0 找到众函数中对应 V 最小的那个,标示其为 G1
loop2:
在 G1 这个函数中找到最大值点(V1,D1),V1 ∝ JS1
然后根据 D1 找到众函数中对应 V 最小的那个,标示其为 G2
....
/--->根据一个函数找到最大点,根据这个点找最小函数-->--\
\____________________________________________/
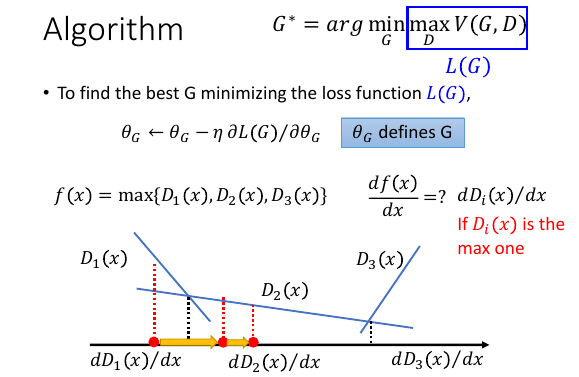 仅仅看 argminG(xxx) 括号里的表达式就相当于 loss-fn,也是用 GD
仅仅看 argminG(xxx) 括号里的表达式就相当于 loss-fn,也是用 GD
问题是表达式里面有 max, 可以用 GD 么,完全可以,之前已经见过至少 3 个 max 都用 GD 来解了。
>>> GD 解 max ------------------------------------------------ 就是看成分段函数,然后做微分即可 这一题,就是看 x 落在哪个区域,然后选择 那个区域最大的 Di ,然后这个区域的微分就用 df/dx = dDi/dx ------------------------------------------------

这个分段函数图像给的真好,每个 Gi 对应无数多个 D 从中找到可以让 V 最大的那个 Di 及其对应的 Vi, 一个 Gi 对应一个 Vi, 无限多个 Vi 对应无限多个 Gi,找到其中最小的 Gi 这是一个很简单的数字大小比较问题,但是回忆一下一开始的那张图,Vi 在找 G 这一步是一个函数。是不同的 Di 加持下的函数: V1(G,D1) V2(G,D2) V3(G,D3) V4(G,D4) V5(G,D5) . . 他们共同组成一个函数 f(x) ,要在这个 f(x) 上找到最小的 G 这就又回到了 GD 优化问题上来了。
.. | G0 ---> D0* .. | / .. | / JS↓ .. | / JS | G1 ---> D1* .. | / .. | / JS↓ .. | / .. | G2 ---> D2* .. v ......
有一个小小的问题
如下 ppt 所示:
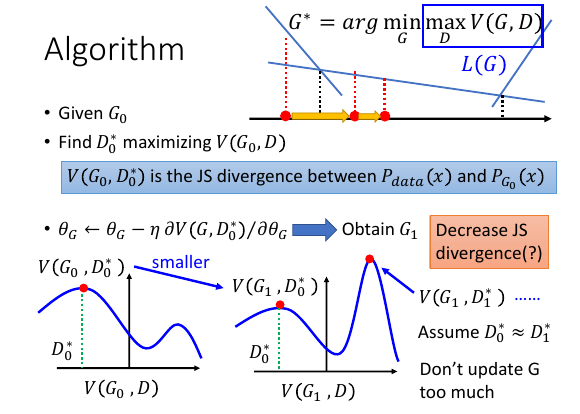 有个比较棘手的问题:我们的步骤是一开始给定 G0, 得到最大化 maxV0 的 D0*
然后固定 D0* 寻找能最小化 maxV0 的下一个 G,将其做为 G1.[下面注意坑来了]
这个新的 G1 就像当于一个新的函数:
有个比较棘手的问题:我们的步骤是一开始给定 G0, 得到最大化 maxV0 的 D0*
然后固定 D0* 寻找能最小化 maxV0 的下一个 G,将其做为 G1.[下面注意坑来了]
这个新的 G1 就像当于一个新的函数:

/--->根据一个函数找到最大点,根据这个点找最小函数-->--\ \____________________________________________/ 在这个新的函数上再寻找能 maxV1 的 D,称其为 D1*. 但这并不能保证 maxV1 > maxV2 之前说过: JS1 ∝ maxV1 JS2 ∝ maxV2 所以 JS1 ?> JS2 因为中间切换了一次函数,不能保证第一个函数的最大值一定比第二个函数的最大值大。 换言之,并不能保证 JS divergence 在逐渐减小。 所以只能假设 D0*≈D1*, 每次 update G 不要太多
6.4.1 逼近期望值
 原来做期望要用积分,现在换成取样 m 个点然后取平均
V~ 这个式子应该很眼熟才对,因为普通的贰元分类就是在 minimize 这个式子
原来做期望要用积分,现在换成取样 m 个点然后取平均
V~ 这个式子应该很眼熟才对,因为普通的贰元分类就是在 minimize 这个式子
6.4.2 最小化误差 = 最大化差距,训练 D
 [勘误] L 表达式应该加个负号。
[勘误] L 表达式应该加个负号。
怎么找一个 D 去 maxV 呢?想想 D 的实际意义,D 是鉴别器,其目标就是鸡蛋里挑骨头---找茬。所以 D 的目标是最大化 PG 和 Pdata 的距离(JSDivergence)
D 的本质是一个贰元分类器,输出一个实数:标示生成图(sample from PG)与样本图(sample from Pdata)的相似性,实数越大表示越像。
分类器如何做最大化?先看分类器的训练集: D 的训练集来自与两个分布, Pdata 的样本标记为 +1, PG 的样本(G 生成的图片)标记为 -1. 再看分类器的 loss-fn: 所有分类器的目标都是减少 loss-fn,增加准确率,增加什么准确率,就是让所有正的都标记正,所有负的都标记负。把所有 +/-1 样本全都拿来散落到图像上,训练 D 知道他能把 +/-1 全都分开,这就是最大化,最大化什么?最大化 +1 -1 之间的差距。
所以 最小化误差 = 最大化差距 如上图 ppt 所示,这在数学上也是一致的:minimize L = maximize V~
然后再使用这个分类器 D(相当于数学公式里固定这个 D), 联合 G 一起 train G, 这时候的目标就是 最小化差距 ,公式还是 V~ 这个公式,但是变量变成 G 了。
取样一些样本作为训练集,去 train 一个贰元分类器,这个分类器的 loss-fn 就是
>>> 分类器如何做最大化 ----------------------------------- 这是一个很神奇的命题,分类器可以做最大化问题 -----------------------------------
6.4.3 算法总览

因为 train 的是一个神经网络,所以有可能 train D 的时候会停在一个 V 的 local maxmization 上。所以我们获得的不一定示 maxV,而仅仅示一个 V 的 lower bound. 而且在 train D 的时候用的是 GD .所以需要执行多次循环 update 来获得微分近似为 0 的点 — Repeat k times。
然后开始训练 G,训练 G 的时候是把 G0+D0* 放在一起训练,但是固定住 D 的参数,然后训练 G 的参数,训练目标呢还是这个 V~,但是变量 variable 从 D 变成了 G,G 出现在哪里呢?出现在 D(xi~),这里的 xi~ 就是从 z 原始 code 进入 G 之后生成的: xi~ = G(zi), 所以整个式子就变成以 G 为变量的式子。D 对待这个式子用的是最大化,现在 G 为了骗过 D(数学上就是固定 D0* 在一堆函数中找一个 V 最小的函数)
ppt 中红线划掉的部分是没有 G 的,换言之训练 G 的时候这部分是常数,不影响最小化 V~
有一个小小的问题 在参考之前讨论的这个小小的问题,update G 不能太大,所以只更新一次否则有可能让 V~ ∝ JSD 变大 –> Learning G Only Once
6.4.4 G 实做时的问题
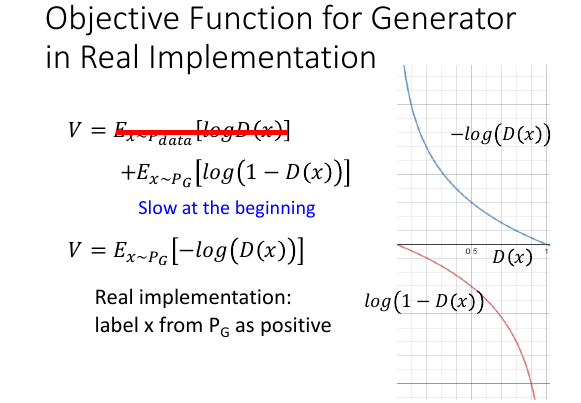 理论上训练 G 的时候,应该 minimize V, 但是在实际做的时候,以及 GAN 发明者论文上也讨论说:似乎不应该最小化 V. 为甚么呢?
理论上训练 G 的时候,应该 minimize V, 但是在实际做的时候,以及 GAN 发明者论文上也讨论说:似乎不应该最小化 V. 为甚么呢?
看 ppt 右边图像,log(1-D(x)) 红线部分,当 D(x) 很小的时候,很平滑;当 D(x) 很大的时候,觉陡峭;D(x)小代表什么,代表生成的图片被识别为【不像】,但是我们开始的时候生成的图片都是【不像】的,所以在训练的初始阶段由于 D(x)太平滑,训练的会很慢。
红线划掉的部分在训练 G 时是常数,所以划掉,上页 ppt 有说明过
所以把 log(1-D(x)) 换成 -log(D(x)) 蓝线部分,当 D(x) 很小时很陡峭,很大时很平滑,而且这两个函数的方向只一致的。
所以,训练 G 时的 V = Ex~PG[-log(D(x))]
这样做还有一个实做时的额外的好处: 让 PG 产生的样本时 positive example(Pdata)
The code used in demo from: • https://github.com/osh/KerasGAN/blob/master/MNIST_CNN_GAN_v2.ipynb
6.5 Issue about Evaluating the Divergence
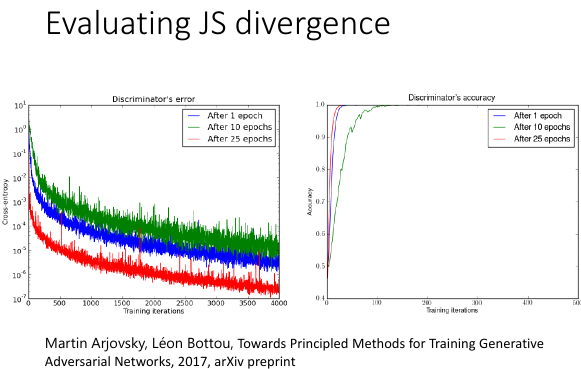 通常情况鉴别器都太猛了,图中三個 G, G with 25 epoch 已经很强,但是丢到 D 中,还是被一眼就看出。D 的正确率几乎就是 100%.
通常情况鉴别器都太猛了,图中三個 G, G with 25 epoch 已经很强,但是丢到 D 中,还是被一眼就看出。D 的正确率几乎就是 100%.
这样的问题是: 本来 D 是来测量 JSD 的,但实际上 D 告诉我们关于 JSD 的信息非常的少。
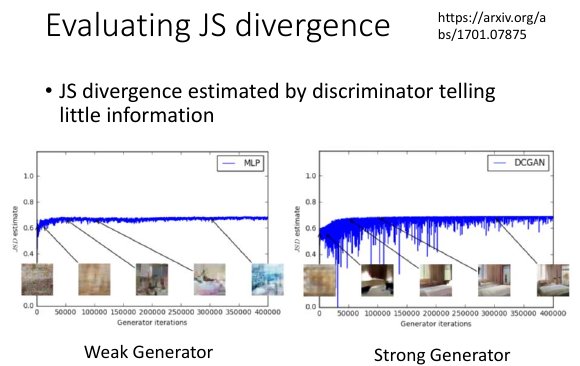
横轴标示第几代的 G, G0,G1,…,G40000 纵轴标示从鉴别器中显示出的 JSD 的度量,可以看到即便时很强的 G 产生出的图片人类都辨别不出真假了, JSD 还是维持一个不怎么变的平缓的值,也就是说 图片变真没有改变 D 所计算的 JSD.
这说明 D 所计算的那个 JSD 没有真实的反映出图片的质量。
为甚么出现这种情况呢?
6.5.1 reason -1
 因为我们之前的用的是 V~ 不是真正的 V
V 是要用积分计算期望,我们没办法做这个,所以退而求其次,
V~ 是用 smaple 之后取平均来模拟这件事情。
因为我们之前的用的是 V~ 不是真正的 V
V 是要用积分计算期望,我们没办法做这个,所以退而求其次,
V~ 是用 smaple 之后取平均来模拟这件事情。
这样做之后,假如两个分布是真的有重叠的部分,但是由于我们使用 V~ 来衡量他们之间的 JSD(换言之衡量的 JSD 是不真实的),由于样本点的分布变的简单了所以 D 总是能找到一条线把他们彻彻底底的分开。
6.5.2 reason -2
 两条直线的交集几乎就是 0.
从 data 的本质上来看,我们考虑的 data 都是高纬度空间中的 manifold
比如我们现在产生的是 image, image 就是高维空间中的 manifold.
两条直线的交集几乎就是 0.
从 data 的本质上来看,我们考虑的 data 都是高纬度空间中的 manifold
比如我们现在产生的是 image, image 就是高维空间中的 manifold.
事实上,你的 G 所产生的 data 也会是高维空间中的 manifold. 比如生成器的输入 z 是 10 维度,输出 x 虽然是 100 维度。但他依然是 100 维度空间中的 10 维度的 manifold.
如果用图像标示的话,如果 generator 产生的 data 的 space 是二维度空间那么 PG 和 Pdata 就是两条线,那么他们的交集就是两个点,也就几乎为 0.
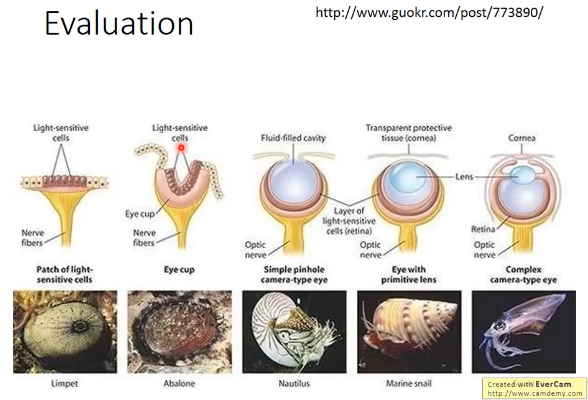
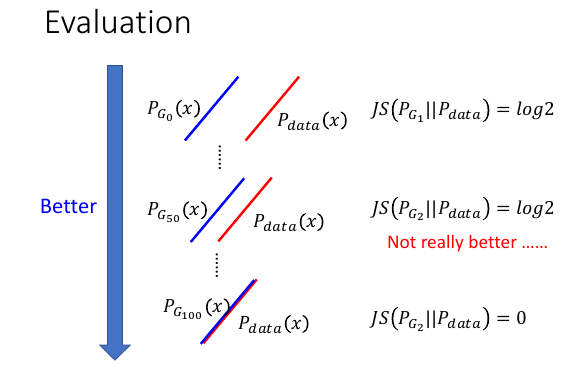
从 JSD 大,到 JSD 小,因为 GD,必须有一个过度的过程,但是这个过程得以成行 的前提条件是:后一代一定比前一代更好,这样才能慢慢进化过去到 JSD=0 PG1 bettern than PG0 PG2 bettern than PG1 PG3 bettern than PG2 PG4 bettern than PG3 .................... 如果中间任何一处出现:PGi+1 not better than PGi. 可是 PGi+1 not better than PGi 在用 JSD 衡量差距时经常出现,如上 ppt 中, PG0||Pdata 是没有交集的,所以 JSD = log2 PG50||Pdata 是没有交集的,所以 JSD = log2 但是 PG50 确实离 Pdata 更近了。这一点没有在 JSD 的数值中反映出来。 这个过程就是戛然而止,这个过程得以成行的条件太苛刻了。
6.5.3 怎么解决这个问题呢?method-1: add noise
WGAN 可以解决这个问题,这里提供另一个简单方法:加入 noise

加入 noise 之后,线就变宽了,就成面了,交集就变大了。实做上 noise 应该随着时间越来越小,避免影响图片生成的不精确。
6.5.4 怎么解决这个问题呢?method-2: mode collapse
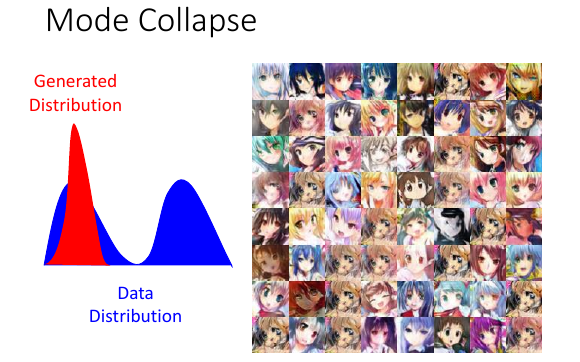 如果 Pdata 是两个高斯,但生成器可能只产生一个高斯出现很多重复的脸,虽然不同的头发。
如果 Pdata 是两个高斯,但生成器可能只产生一个高斯出现很多重复的脸,虽然不同的头发。
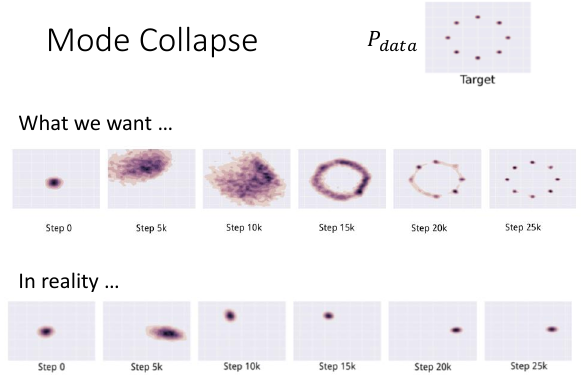 陷入一种 猫抓老鼠 的情况
陷入一种 猫抓老鼠 的情况
6.5.5 为甚么出现上面两中 mode collapse 的情况呢?
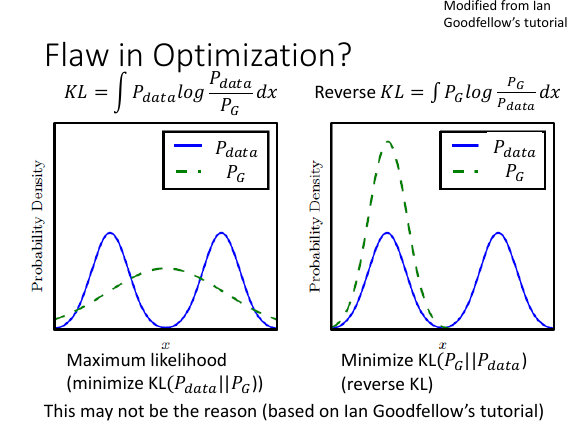 李老师讲了很多,但是我没有记。
李老师讲了很多,但是我没有记。
6.6 So many GANS

6.7 Conditional GAN
<MLDS 要做这个>
Scott Reed, Zeynep Akata, Xinchen Yan, Lajanugen Logeswaran, Bernt Schiele, Honglak Lee, “Generative Adversarial Text-to-Image Synthesis”, ICML 2016 Han Zhang, Tao Xu, Hongsheng Li, Shaoting Zhang, Xiaolei Huang, Xiaogang Wang, Dimitris Metaxas, “StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks”, arXiv prepring, 2016 Scott Reed, Zeynep Akata, Santosh Mohan, Samuel Tenka, Bernt Schiele, Honglak Lee, “Learning What and Where to Draw”, NIPS 2016
Conditional GAN 就是要控制你的生成器。
6.7.1 Text to Image
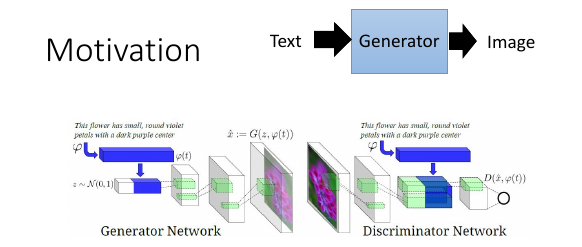
假设我们要 input 一个名词,产生一个这个名词对应的图片。
>>> 教授说这是一个 supervised learning ------------------------------------ 这个意思是,图片是标签,文字是数据? 原来监督学习还可以用图片做标签的? 我到现在才知道啊~~~~~~~~~~~~~~ ------------------------------------ >>> 这里体现了 GAN 和 supervised learning 的不同就 --------------------------------------------------------- 那为甚么一定要用 GAN 而不用 supervised learning 呢? 用监督学习的话,input 是一个点,output 也是一个点。 *而不是一个分布* - 监督学习:input a point, output a point - GAN : input a distribution, output a distribution 什么意思呢? 就是监督学习太死板了! ---------------------------------------------------------
给 train 打图片标签,打 6 个图片标签当用监督学习的时候,他会 output 的是一个最小化到 6 个图片标签的距离均值的图片,他本身根本不像图片,而仅仅是 6 个图片像素的均值而已,他会非常模糊。
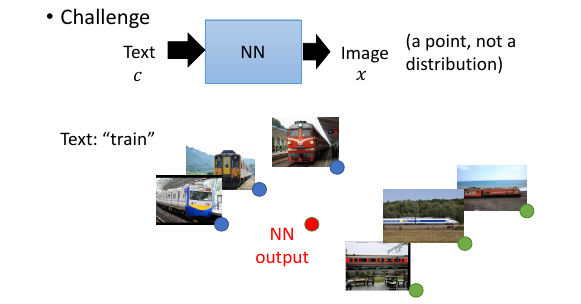
CGAN 在实做的时候有个小坑 Prior distribution z 有时候会被 GAN 直接忽视,把他当作 noise . 也就是说 CGAN 经常出现给定 C 的时候不管 z 是什么分布最后的结果都一样。
如何解决这个问题?不一定要 input 一个 distribution,只要能在 outpu 产生一些 random 效果即可。所以一个方法是加入 dropout,使他无法忽视 z.
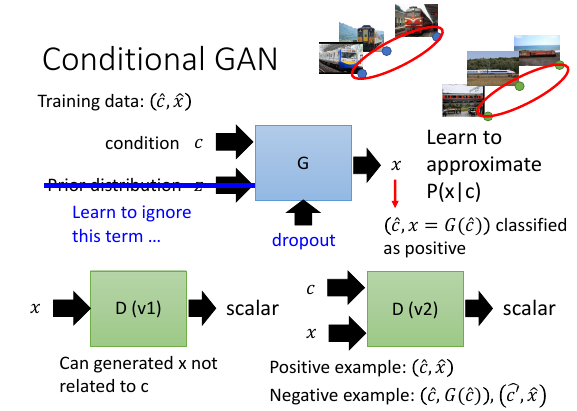
在 CGAN 里面鉴别器有两种版本: x 是一张图片,c 是壹段描述
- x –D–> scalar : 他能学会如何生成【像的】图片,但 没法 学习如何生成【符合 C 描述的】图片
- x,c –D–> scalar ✓
这里选择 2) 版本的鉴别器,但训练这个鉴别器的样本更复杂:
- positive example: (C✓,x✓) positive 样本不用说了肯定是训练集中已经存在的(描述,图片)对
- negative example: (C,G(C)), (C×,x✓) negative 样本不但要包含跟普通 GAN 一样的生成图,还要包含原来样本集中(瞎吊描述,正确的图)这样的样本
6.7.2 Text to Image result
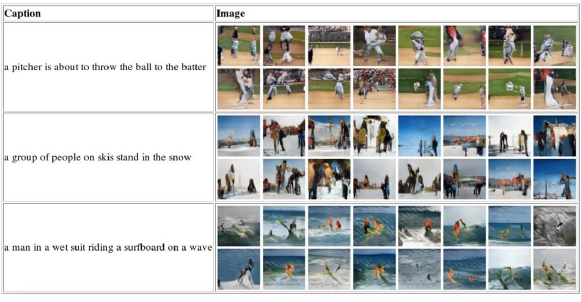
6.8 Image to Image Translation
略 Phillip Isola, Jun-Yan Zhu, Tinghui Zhou, Alexei A. Efros, “Image-to-Image Translation with Conditional Adversarial Networks”, arXiv preprint, 2016

7 2) Unified Framework
7.1 review basic idea
The data we want to generate has a distribution Pdata(x) 我们认为我们要生成的点来自于一个概率分布,这里的 x 可以是任何东西,图片,句子,视频等等。
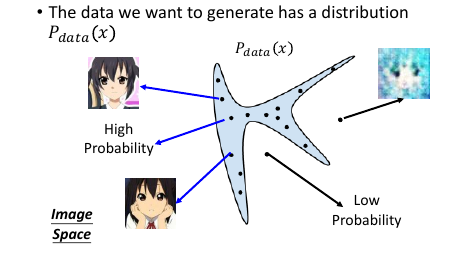 假设蓝色部分是 Pdata 概率较高的部分,蓝色区域以外是概率较低的部分。从概率高的部分 sample 出的图片就像模像样,概率低 sample 出的图片就很模糊。
假设蓝色部分是 Pdata 概率较高的部分,蓝色区域以外是概率较低的部分。从概率高的部分 sample 出的图片就像模像样,概率低 sample 出的图片就很模糊。
输入一个 Normal Distribution 经过一个 GAN 生成一个 复杂且未知的 Distribution. 我们希望调整 NN 的参数,来让生成的 PG 跟 target distribution Pdata 越接近越好。
但是难点在于,我们没办法直接计算 PG(x),给定一个 x 没法算出 PG(x) 是多少,如果能算出 PG(x) 就可以使用 Maximize Likelyhood. 也就是说给你一张图片,我根本不知道 GAN 产生这个图片的概率值是多少。
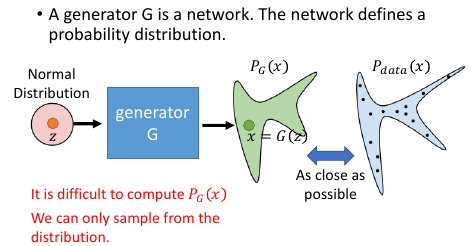 唯一能做的事情只剩下 sample. 从 z: normal distribution 中 sample 一些点
唯一能做的事情只剩下 sample. 从 z: normal distribution 中 sample 一些点
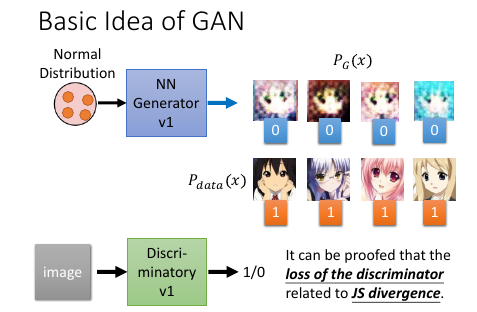
7.2 Intuition
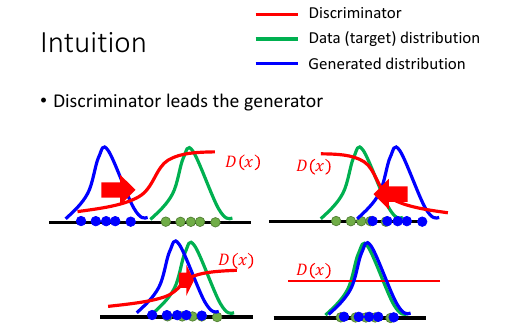
一开始的分布是如图,产生一个 D1(X):使得靠近绿色分布的地方输出高,蓝色地方的输出低蓝色分布会向右边移动, 移动的过程中有可能跑过头,然后训练一个新的 D2(x):仍旧是绿色函数值高,蓝色低函数值 …… Di(x): 随着蓝色分布和绿色分布重合的越来越多,Di(x) 会越来越平缓直到最后,两者重合,Di(x)变成一条直线。
7.3 Unified Framework
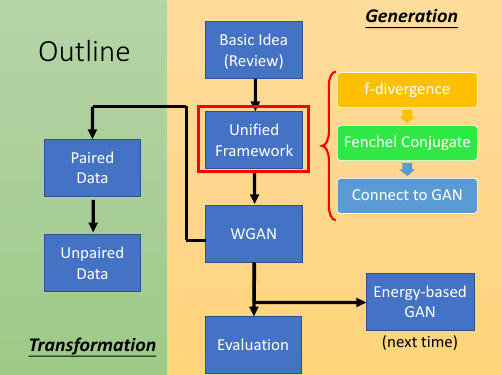
7.4 f-divergence
• Sebastian Nowozin, Botond Cseke, Ryota Tomioka, “f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization”, NIPS, 2016 • One sentence: you can use any f-divergence
Basic Idea 讲的是 GAN 与 JSD 有关,但你可以重新定义 V 定义完全不同的 divergence

f-divergence 定义了一个 divergence 框架,上面的公式 f 可以是任何的函数,只要满足:
- f is convex
- f(1) = 0
这两个条件即可。
-------------------------------------------------- 下面的这个 convex f 的转换是这节课的重点,不理解也要背诵下来: ∫qf(p/q)dx >= f(∫q(p/q)) = f(1) = 0 --------------------------------------------------
7.4.1 KL-divergence is a f-divergence
| f = xlogx | KL | | f = -logx | Reverse KL | | f = (x-1)^2 | Chi Square |

7.5 Fenchel Conjugate
 每一个 convex function 都有一个‘伙伴’叫做 conjugate
每一个 convex f 都有一个同源函数 f*
这里的 f* 的感觉有点像是上一节 basic idea 中 G&D 的取值方式先固定函数 G 在 G 里找一个最大值 D,然后固定 D,在所有的函数中找最小值。
每一个 convex function 都有一个‘伙伴’叫做 conjugate
每一个 convex f 都有一个同源函数 f*
这里的 f* 的感觉有点像是上一节 basic idea 中 G&D 的取值方式先固定函数 G 在 G 里找一个最大值 D,然后固定 D,在所有的函数中找最小值。
这里也是假设给定一个 t1: f*(t1) = max{xt1 - f(x)} 也就固定了一个函数:xt1 - f(x) 从这个函数中找到最大值:x1
如果给定另一个 t2: 也就固定了另一个函数:xt2 - f(x) 从这个函数中找到最大值:x3
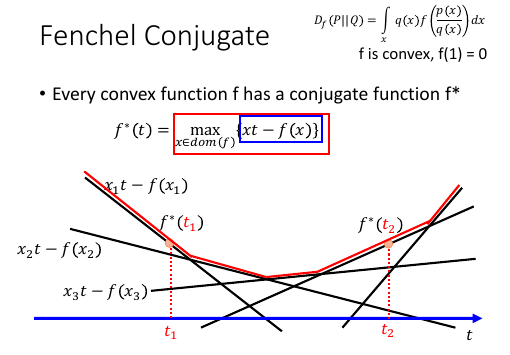 如果没有给定 t,而是给定 x 呢?那么 max 里面那部分就只是 3t - 2 这种形式, 也就是一个线性函数而已。不同的 x 会对应不同的线性函数。
如果没有给定 t,而是给定 x 呢?那么 max 里面那部分就只是 3t - 2 这种形式, 也就是一个线性函数而已。不同的 x 会对应不同的线性函数。
下面就给定一个 t, 看看哪个函数可以给你一个最大值。比如给定 t1, 照着他画一条直线,看看切过的所有线性函数里哪一个最大。就选那个函数。最后构成一个凸函数:f*(t)
所以也把这个函数背下来吧,整个函数的意思就是: 用小树枝搭一个鸟巢,用最上面那一层 f'(t) = max(xt - f(x))
t 作为未知数,给定不同的 x 值,就会根据 xt-f(x) 产生不同的直线。每一个 t 值都对应无数个 x, 每一个 x 都对应一个线性函数。每一个 t 值都从无数个线性函数中挑一个最大的。
7.5.1 看看 f(x) = xlogx 的同源函数
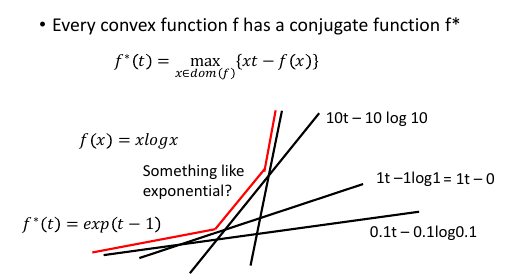 一个 t 对应无数个 x, 一个 x 对应一條直线.
可以看到 xlogx 的同源函数似乎长的有点像 exponantial fn
一个 t 对应无数个 x, 一个 x 对应一條直线.
可以看到 xlogx 的同源函数似乎长的有点像 exponantial fn
7.5.2 证明 xlogx 的同源函数是 exp(t-1)
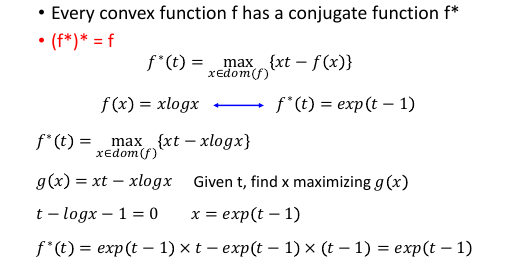
固定 t, 看 x 变动的时候,哪个 x 能让 g(x) 取最大值。
怒微一发, ∂g/∂x, 当微分等于 0 的时候,就可以得到极值。
最后得到 x = exp(t-1) 带入原式,就可以去掉 max 符号了。
f*(t) = xt - f(x)
= exp(t-1)*t - exp(t-1)*log(exp(t-1))
= exp(t-1)
>>> 背下来 conjugage 函数的性质 ----------------------------- (f*)* = f 同源函数与原始函数之间是可以互逆的。 -----------------------------
7.6 f-divergence + conjugate + GAN
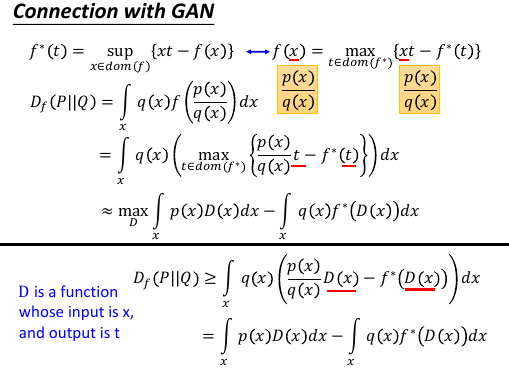 因为凸函数存在一个同源函数,所以我们可以把 f-divergence 里的可以随便设置只要满足两个条件
1.convex 2.f(1)=0 的这个 f 置换成 他的同源函数的表达式: f(x) = max{xt - f*(t)}
因为凸函数存在一个同源函数,所以我们可以把 f-divergence 里的可以随便设置只要满足两个条件
1.convex 2.f(1)=0 的这个 f 置换成 他的同源函数的表达式: f(x) = max{xt - f*(t)}
置换之后,把 t 用 D(x) 取代,怎么跑出来一个 D(x) 呢? 暂时不要想這些,只需要直到 D 是一个函数,输入 x 输出 t: t = D(x), 但是没法保证这里的 D(x) 输出的 t 可以让上面的式子 max. 所以这里用一个 >= ,表式这是一个 lower bound.
因为带 D 的表达式是 f-divergence 的 low-bound, 如果我能最大化这个 带 D 的表达式,他不就逼近 f-divergence 了么。 所以下面的工作就是:argMaxD(xxx). 找到一个可以让 low-bound 最大的 D.
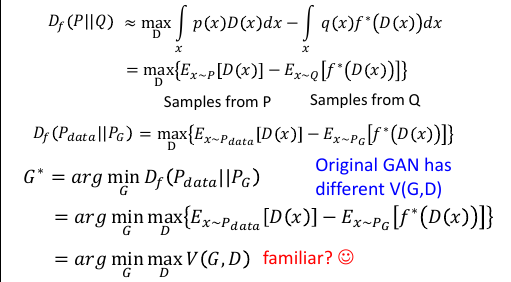
>>> 我去!如何从高数到概率,这个转换数次用到,很重要 ------------------------------------------ 怎么把积分变成期望再变成取样: 做期望值这件事情可以用取样来近似 积分 ---> 期望 ---> 取样 ∫p(x)f(x)dx = Ex~p[f(x)] ≈ samples from p ------------------------------------------
实际做的时候没法算积分,所以只能用 sample 的方法来近似了。到这里既可以看看 basic idea of GAN 了。
>>> 如何定义 V ------------------------------------------------------ 这里是类似的,只是在 basic idea of GAN 中没有指明 V 是从哪来的。 这里可以看出,V 是如何定义的: 找出一个 convex-fn f, 找到他的 conjugate-fn f* 把他们带入 Ex~pdata[D(x)] - Ex~pG[f*(D(x))] 就可以了 ------------------------------------------------------
7.7 Double-loop v.s. Single-step

>>> double-loop algo
---------------------
give G0
loop: to get (Gi+1,Di)
loop: to get D0
once: to get G1
---------------------
>>> single-step algo
-----------------------
give G0 D0
loop: to get (Gi+1,Di+1)
once: BP,D↑
once: BP,G↓
-----------------------
感觉 single-step algo 不但实做简单,而且更容易理解:
每一次 D 要朝着让 V 变大的方向走一步
G 要朝着让 V 变小的方向走一步
7.8 many f-divergence
7.9 Minimize 不同的 divergence 有什么差别
当 Generator 不够强的时候,确实会有差别比如当你想要用一个高斯来逼近混合高斯时,minimize 不同的 divergence 会产生完全不同的近似结果。
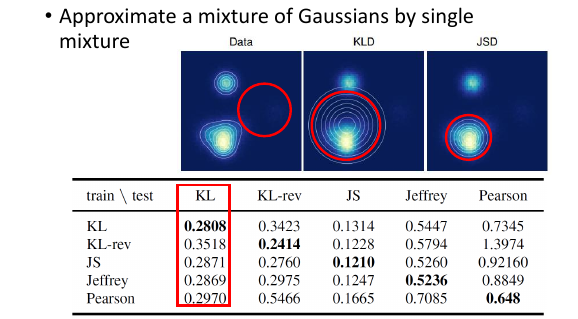 可以看到,当 data 分布是由两个高斯产生的时候,
minimize JSD 会让近似的高斯很【偏激】
minimize KLD 会让近似的高斯很【中庸】
可以看到,当 data 分布是由两个高斯产生的时候,
minimize JSD 会让近似的高斯很【偏激】
minimize KLD 会让近似的高斯很【中庸】
这也让一个认识被【证误】了: ----------------------------------------------------------------------------- × 过去大家都认为 GAN 生成的图片总是【太集中,多样性不够】是因为我们选取的最小化目标 V 是 JSD -----------------------------------------------------------------------------
但通过下面那张表可以说明:(这里我没听懂,为甚么那张表可以说明 不论用哪个 divergence 生成的图片都会很集中,很没有多样性)
8 3) WGAN
Reference • Martin Arjovsky, Soumith Chintala, Léon Bottou, Wasserstein GAN, arXiv prepring, 2017 • Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville, “Improved Training of Wasserstein GANs”, arXiv prepring, 2017 • One sentence for WGAN: Using Earth Mover’s Distance to evaluate two distributions • Earth Mover’s Distance = Wasserstein Distance
一句话概括 WGAN: 普通的 GAN 是 minimize f-divergence WGAN 是 minimize Earth Mover's Distance
8.1 Original version (weight clipping)
8.1.1 Earch Mover's Distance
https://vincentherrmann.github.io/blog/wasserstein/ 如果课程哪里不懂,直接看这篇 blog,非常棒,李老师推荐
推土机把土堆 P,推到 Q 位置,推土机要移动多少距离。
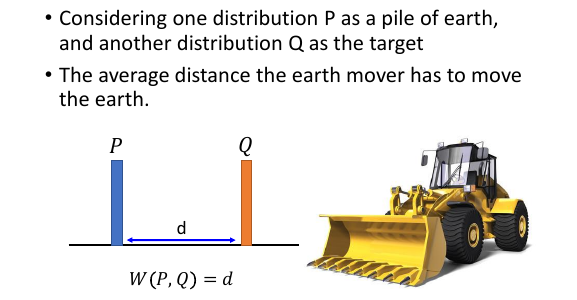
如果要把 P 的土,铲成 Q 的样子,有很多‘moving plan’用不同的 moving plan 就会有不同的 distance 用 distance 最小的 moving plan 来定义 movers' distance
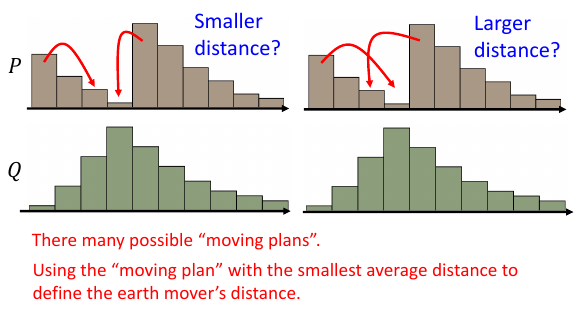
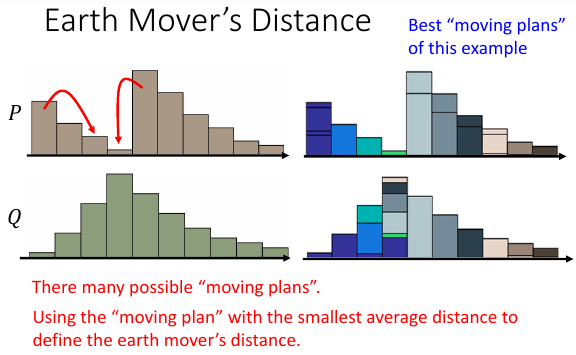
8.1.2 矩阵表式下的 moving plan
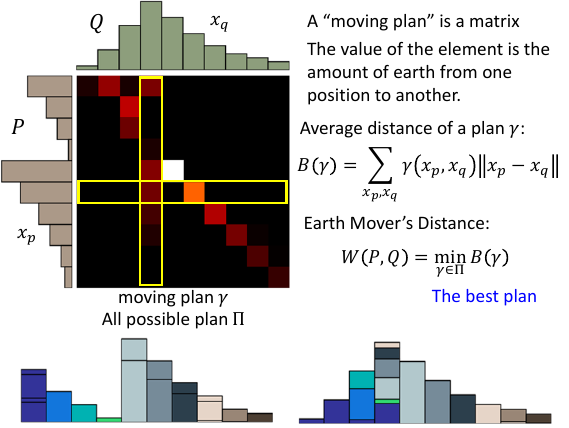 这个矩阵的每一个位置的值都是从(行->列)的土量
这个矩阵的每一个位置的值都是从(行->列)的土量
>>> 推土距离释疑 ------------------------------------------------ 这里一定注意,之前表述不是很清楚,不是把 P 土堆推到 Q 土堆。 而是就在 P 土堆这里把土推成 Q 的形状。 ------------------------------------------------
矩阵的每一个位置的值是推土量这个矩阵如何表示推土距离呢?
Q
1 2 3 4 5
+--------+--------+--------+--------+--------+
| | | | | |
1 | | | | | |
+--------+--------+--------+--------+--------+
| | | | | |
2 | | | | | |
+--------+--------+--------+--------+--------+
P | | | | | |
3 | | | | | |
+--------+--------+--------+--------+--------+
| | | | | |
4 | | | | | |
+--------+--------+--------+--------+--------+
| | | | | |
5 | | | | | |
+--------+--------+--------+--------+--------+
如图:P1 -> Q1 其实就是,P1 通过各种土的移动最终形成 Q1 的形状所以距离就是行号列号之差: 行号-列号
注意: 土量 就是 概率
注意: 这个矩阵每一个 row 的意义是什么?表示从这个位置移出去到其他位置的土量的和比如 P3 那一行的和,就表示从 P3 移动到 1,2,3,4,5 五个位置的土量各是多少。他们的和就应该是 P3 所持有的总的土量。土量是什么,就是概率,所以 P3 那一行的概率的和,就应该等于 P3 的概率
注意: 这个矩阵每一个 column 的意义是什么?每一个 column 表示所有进入到这一列最终形成 target 形状的所有土量。比如 Q2 最终形成就是依靠 1,2,3,4,5 五个位置的‘进贡’形成的。这个 Q2 的土量就是所有 5 个位置的进贡之和。所以 Q2 的概率也是那一列所有五个位置的概率之和。
注意:一个矩阵就代表一个 moving plan 一个 moving plan 用 γ 表示, 所有可能的 moving plan 的集合用 Π 表示
某一个 moving plan γ 的平局移动距离是多少呢?γ(xp,xq) 表示从 xp 移动到 xq 的土量 B(γ) = Σ 总移动土量 * 单位土量的移动距离 B(γ) = Σ γ(xp,xq) * ||xp - xq||
Earth Mover's Distance 是什么,就是 Π 中 B(γ) 最小的 γ W(P,Q) = min B(γ) 穷举所有可能的 γ,选取其中 B(γ) 最小的
8.2 Why Earch Mover's Distance
8.2.1 提供进化的两个条件
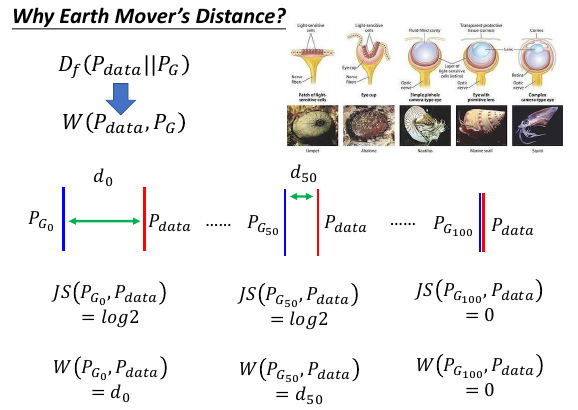
Df(Pdata || PG) –>换成--> W(Pdata, PG)
最小化两个分布的差异,像是进化,而进化的条件是:
- 改变需要循序渐进的 JSD 的值很跳跃
- 每一点改变都应该有【好处】 JSD 有时候并没有提供‘进步的好处’
而 JSD 提供不了 '循序渐进的提供好处' 这个特征所以在利用 JSD 作为进化圭尺的时候会不断卡住
而 Earth Mover's Distance 却可以同时满足两个进化条件:
- 土量×单位土量的移动距离 值很平缓的变化
- 土量×单位土量的移动距离 值一直在增大
8.2.2 可以用 GAN 表示这个 EMD
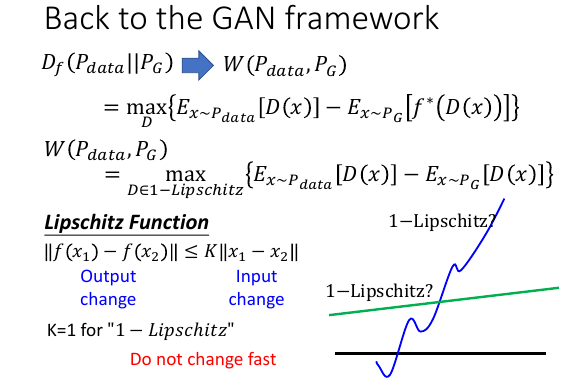 f-divergenc 可以写成两个期望的差值,D 是一个 NN 表示的函数,想是什么样的都可以
W(Pdata,PG) 确实也可以写成两个期望的差值,但是 D 不是随便取的,而是必须在
1-Lipschitz 这个 set 中。
f-divergenc 可以写成两个期望的差值,D 是一个 NN 表示的函数,想是什么样的都可以
W(Pdata,PG) 确实也可以写成两个期望的差值,但是 D 不是随便取的,而是必须在
1-Lipschitz 这个 set 中。
8.2.3 引入 Lipschitz Function
Lipschitz Function: 输出的变化 小于 输出变化的 K 倍也就是说这个 lipschitz-fn 不是一个变化很猛烈的函数 1-Lipschitz function: K = 1 一个变化比较缓慢的函数上页 ppt 显然绿色是 1-lipschitz 函数
8.2.4 为甚么需要 1-Lipschitz 限制呢
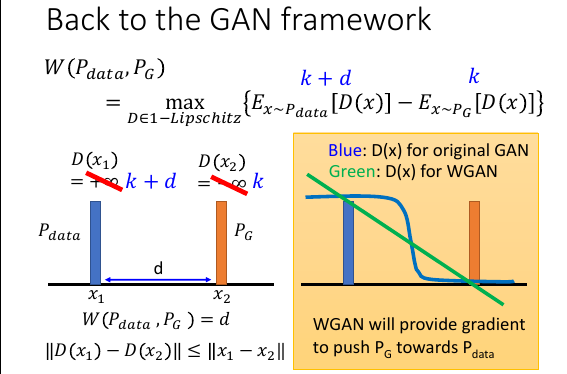 如果没有 1-Lipschitz 来限制 D 的话。D(x1) = +∞ D(x2) = -∞ 就是最大的。加上这个限制的话,如果 x1 x2 相距 d, 那么 D(x1) D(x2)最大差距也只会是 d.
如果没有 1-Lipschitz 来限制 D 的话。D(x1) = +∞ D(x2) = -∞ 就是最大的。加上这个限制的话,如果 x1 x2 相距 d, 那么 D(x1) D(x2)最大差距也只会是 d.
从黄色图中,也可以窥得为甚么要把 JSD 换成 W(pdata,Pg) 在普通 GAN 里面 D 是一个贰元分类器,他的 output 是一个 sigmoid 函数。如果想把 Pdata 分布与 PG 分布分开的话,D(x) 需要在蓝色的位置约等于 1;D(x) 需要在橙色的位置约等于 0. 问题是在两头的位置都太平滑了。如果我们今天要找的 D 换成用 W(pdata,pg)来衡量差距,既要让蓝绿两色差距最大,而且还要符合 1-Lipschitz 的话。 找出来的 D(x) 的激活函数, 有可能是绿色的直线。这样 GD 可以很容易顺着这个方向朝目标分布移动。
8.2.5 如何使用 1-Lipschitz 这个限制:weight clipping
 weight clipping: Force the weights w between c and -c
After parameter update, if w > c, then w=c; if w<-c, then w=-c
weight clipping: Force the weights w between c and -c
After parameter update, if w > c, then w=c; if w<-c, then w=-c
这个 weight clipping 在训练 RNN 的时候也会做限制这个 w ,也就是相当于限制住了 output, 可以证明的是经过 weight clipping 之后的 D 满足 K-lipschitz, 但是我们要的是 1-lipschitz 然后还可以证明当 D 满足 K-lipschizt 时可以得到一个 K*W(Pdata,PG) 所以用 weight-clipping 来限制 D 的 weight,这样可以把 D 限制在 K-lipschitz, 然后得到的 W(Pdata,PG) 应该除以 K,因为他是 1-lipschitz 的 K 倍
注意: 用 weight-clipping 能保证 D 在 k-lipschizt 中,但这不是说所有的符合 K-lipschizt 限制的 D 都能被 weight-clipping 涵盖。这是一个单向的关系:weight-clipping ==> D in k-lipchizt
8.2.6 如何通过 JSD or mover's distance 看模型数值上的结果
之前有讨论过,JSD 无法正常的反映模型的好坏,如果单单把 JSD 的值拿出来,即便肉眼看上去生成器产生的图片已经非常非常好了,JSD 的值仍然是 log2(代表鉴别器认为差距仍然没变,依旧最大)
用 WGAN 之后就可以通过 mover's distance 来从数值上估计模型的结果。他是真的在如实衡量两个分布的 distance,确实可以看出这个模型的好坏。这样 WGAN 就可以通过 鉴别器的 loss 来判断生成器是否足够好
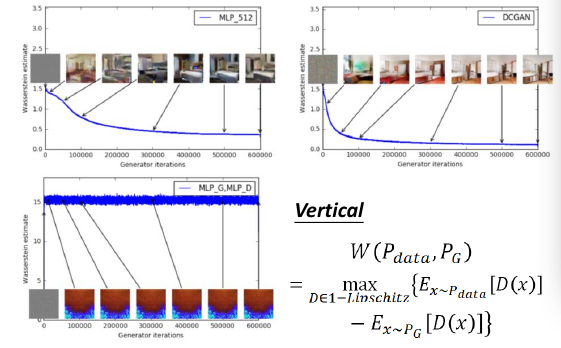 上面两张图,是用 mover's distance 下面是用 f-divergence.
三张图都是 D 的 loss: 纵轴;G 的迭代代数:横轴。
上面两张图,是用 mover's distance 下面是用 f-divergence.
三张图都是 D 的 loss: 纵轴;G 的迭代代数:横轴。
8.2.7 Algo of WGAN

变成 WGAN 算法如下

D:
f-divergence ---> mover's distance
Df(Pdata,PG) ---> W(Pdata, PG)
max{Ex~Pdata[logD(xi)] - Ex~PG[log(1 - D(x~i))]} ---> max_D in 1-L{Ex~Pdata[D(xi)] - Ex~PG[ D(x~i)]}
sigmoid make D(xi) in (0,1) ---> No need sigmoid
No weight clipping ---> weight clipping
Learning D, logD(xi) ---> D(xi)
G:
log(1-D(G(zi))) ---> D(G(zi))
Optimization:
不要用 Adam not used 应该用 RNSpop
8.2.8 试验结果
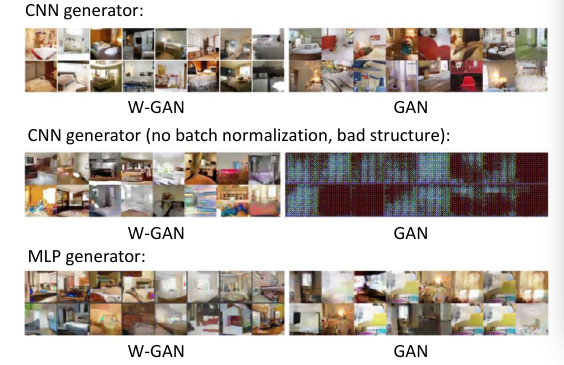
9 Improved version (gradient penalty)
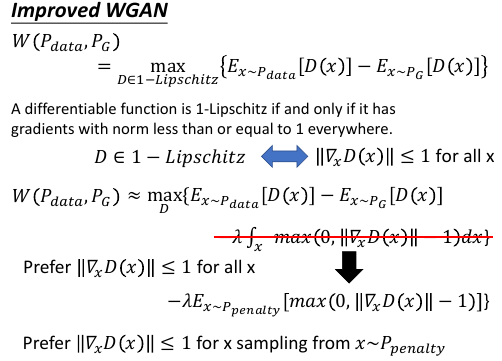
这个改进是针对,【如何对 D in 1-Lipschitz 近似】这件事情:
普通的 WGAN 是通过 weight clipping 来近似这件事情
weight clipping ----> D ∈ 1-Lips
改进的 WGAN 是通过 gradient penalty 来近似这件事情
//∇xD(x)// <= 1 <----> D ∈ 1-Lips
注意这里不是 D 这个 NN 对其参数 w 的 gradient
而是对 x 这个输入的 gradient
这个 gradient penalty 是很直觉的。
这个 gradient penalty 可以通过在 W 的计算公式中追加一个约束项来做到。
这个约束项会在 //∇xD(x)// <= 1 时整体返回 0 , 返回 0 就代表不违反规则,不惩罚
这个约束项会在 //∇xD(x)// > 1 时整体返回 正值, 返回 正值 就代表违反规则,要惩罚
违反规则的意思是说:
//∇xD(x)// > 1 <----> D ∈ >1-Lips
也就是 D 的输出浮动太大
 D 的输出浮动太大也就是 D 最后的斜率太高,如上图中示:所以这里需要【拉近】Pdata 和 PG 的距离来 fit 这个高斜率的绿色线
D 的输出浮动太大也就是 D 最后的斜率太高,如上图中示:所以这里需要【拉近】Pdata 和 PG 的距离来 fit 这个高斜率的绿色线
gradient penalty 和 weight clipping 是从两个角度来解决这个问题: --------------------------------------------------------- 1. weight clipping 是削减 D 的斜率 2. gradient penalty 是拉近 Pdata 和 PG 的距离 ---------------------------------------------------------
但是这个积分是没法求的,所以老规矩---【积分没法求就用 smaple 凑】猛一看这个 Ppenalty distribution 似乎应该是一个 uniform distribution 但其实不是的,原论文中给出的 Ppenalty distribution 另有玄机。
9.1 Ppenalty Distribution
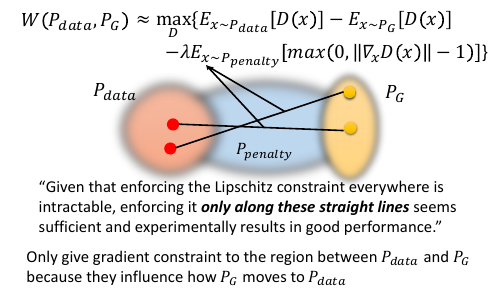 如何 sample Ppenalty 点?
如何 sample Ppenalty 点?
- 从 Ppenalty 和 PG 各 sample 一个点
- 两个点连线,再从线上 sample 一个点作为 Ppenalty 点
可以想成 Ppenalty 就是介于 Pdata 和 PG 之间的一个分布
原 paper 给出为甚么这么做的解释:
“Given that enforcing the Lipschitz constraint everywhere is intractable, enforcing it only along these straight lines seems sufficient and experimentally results in good performance.”
李老师给出为甚么这么做的解释:
Only give gradient constraint to the region between P data and P G because they influence how P G moves to P data
鉴别器 D 的作用是什么,就是引导生成器分布 PG 挪向 Pdata. 所以真正重要的是 Pdata 和 PG 之间的连线的斜率才会真正影响这个‘挪动’。而连线以外的事情就算有影响也是小的。所以仅仅关注 Ppenalty 分布中处在 PG 和 Pdata 之间连线的部分。
9.2 所以再进一步,修改 W(pdata,pG)
与 max(0,//∇xD(x)// - 1) 相比我们更希望 ∇xD(x) 越接近 1 越好。

回忆一下我们对于 D(x) 的期望,我们希望他可以做到很好的【辨别】出 Pdata 和 PG
两个分布的点,借以【引导】G 生成器来优化自己。所以单就【辨别】这个目标来看,我们
希望:D(x) (x 假设是图片)
1) 当 x 处在 Pdata 附近时 D(x)值越大越好;
2) 当 x 处在 PG 附近时 D(x)值越小越好;
1) + 2) ====> D(x) 斜率要足够大
但是由于之前的限制(g radient penalty),我们不希望 D(x) 太陡峭,也就是 D(x)
的 gradient <=1. 所以:
//∇xD(x)// -> 1 <===> (//∇xD(x)//-1)^2 -> 0
“One may wonder why we penalize the norm of the gradient for differing from 1, instead of just penalizing large gradients. The reason is that the optimal critic … actually has gradients with norm 1 almost everywhere under Pr and Pg” (check the proof in the appendix)
“Simply penalizing overly large gradients also works in theory, but experimentally we found that this approach converged faster and to better optima.”
9.3 比较 weight clipping 和 gradient penalty 的实际效果
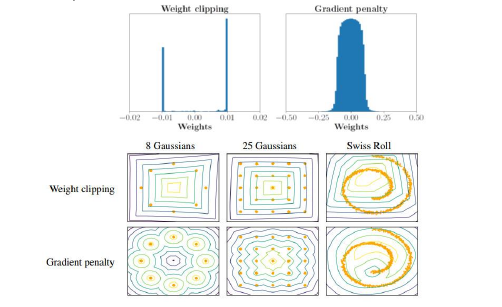


9.4 Improved WGAN Sentence Generation
之前的例子是:
sentence -> _image_
现在我想做一个类似 chat-bot 的东西,它可以:
sentence -> _sentence_
怎么做呢?前面不用动,我只要能把 sentence 也表示成一个 'image' 就可以了。
image 可以是固定大小的 matrix, sentence 怎么变成 matrix 呢?
回忆如何把一篇文章构造成一个长向量,bag of word 是把整个常用英文词典
构成一个长向量,每个单词出现的次数就是长向量相应位置的值。这个向量得以成型的重要
原因是词典的【长度是固定】的,一整个长向量就代表一篇文章。
对 'good bye.' 用 one-hot encoding, 如果把【句子的长度给定住】---句子
的长度按字母和符号个数度量, 每个字母和符号都可以代表长向量的一个位。那么一个定
长的句子,就可以【句子长度×每个字母的句子长度向量】这样一个正方矩阵来表示。
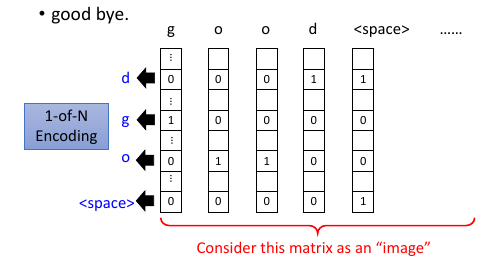
句子不可能都是一样长的,该怎么办呢?这个简单,把句子长度设置 1000 个字母,然后如果句子短,不够 1000 的部分全部用一个自己规定的‘null’的 one-hot encoding 来补全就可以了。
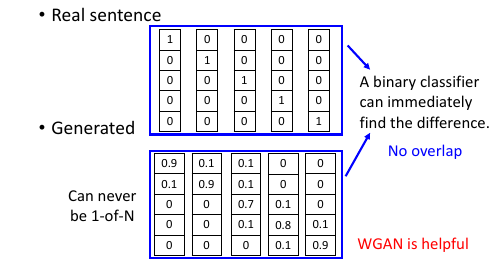 还一个问题:真实的句子都是每一个位置是 1 or 0 的矩阵,而通过 GAN 来训练的时候,目标字母分布是一个概率,我们生成的矩阵可能都是概率,0.1 or 0.9 这样的。就算加 soft-max 来让大的更大小的更小,也没法让小的变成 0.
这样又会遇到与 image generation 一样的问题:JSD 太跳跃了,导致所有从 G
生成的句子都会被 D 认为是假的。
WGAN 出现来解决这种情况。
还一个问题:真实的句子都是每一个位置是 1 or 0 的矩阵,而通过 GAN 来训练的时候,目标字母分布是一个概率,我们生成的矩阵可能都是概率,0.1 or 0.9 这样的。就算加 soft-max 来让大的更大小的更小,也没法让小的变成 0.
这样又会遇到与 image generation 一样的问题:JSD 太跳跃了,导致所有从 G
生成的句子都会被 D 认为是假的。
WGAN 出现来解决这种情况。
9.4.1 唐诗生成

9.5 More about Discrete Output
•••SeqGAN
• Lantao Yu, Weinan Zhang, Jun Wang, Yong Yu, SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient, AAAI, 2017 • Jiwei Li, Will Monroe, Tianlin Shi, Sébastien Jean, Alan Ritter, Dan Jurafsky, Adversarial Learning for Neural Dialogue Generation, arXiv preprint, 2017
•••Boundary seeking GAN • R Devon Hjelm, Athul Paul Jacob, Tong Che, Kyunghyun Cho, Yoshua Bengio, “Boundary-Seeking Generative Adversarial Networks”, arXiv preprint, 2017
•••Gumbel-Softmax • Matt J. Kusner, José Miguel Hernández-Lobato, GANS for Sequences of Discrete Elements with the Gumbel-softmax Distribution, arXiv preprint, 2016 • Tong Che, Yanran Li, Ruixiang Zhang, R Devon Hjelm, Wenjie Li, Yangqiu Song, Yoshua Bengio, Maximum-Likelihood Augmented Discrete Generative Adversarial Networks, arXiv preprint, 2017
9.6 4) Evalution
10 5) Energy-based GAN
回忆之前关于 G 和 D 关系的内容:
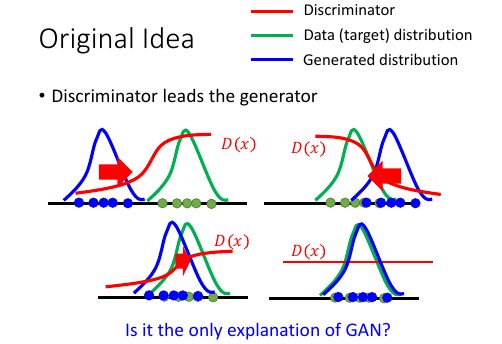
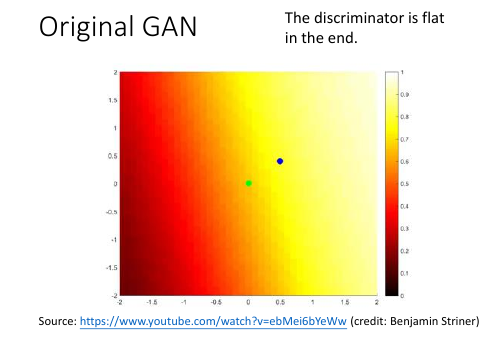
之前所有的 G 和 D 的关系都是:D 是输出 scala 来引导 G 生成让 D 输出更高的 scala 的图片。也就是说,D 只是给 G 生成的图片打个分。G 需要很复杂,而 D 的输出就是【一维度】的。
但是,也许这不是 GAN 唯一的结构。回忆 structure learning.
10.1 Evaluation Function
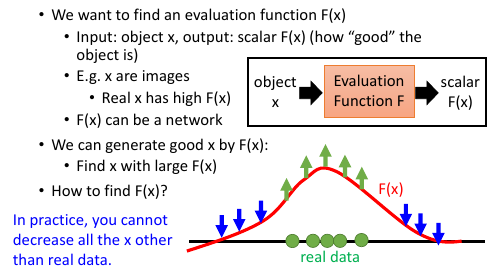
这里的想法是这样的:
找一个 F(x),Pdata 的图片让他的值很高,PG 的图片 让他的值比较低,找到
一个能让 F(x) 很大的 x,然后我就能通过 F(x) 来产生图片。
我们之前的想法是这样的:
我们有一堆已经准备好的图片,我们假设这些图片都是出一个分布种取样出来的。
既然可以取样出来至少说明,他们再这个分布中的概率比较高,所以我们给出这样的推断:
符合人的逻辑和审美--》取样出来的--》概率高
不符合人逻辑和审美--》取样出来的--》概率低
也就是说,我们手上的图片处于这个分布的高概率区域,而没有的那些图片,那些不符合
逻辑和审美的图片处于低概率区域。
但是我们不知道这样一个分布是什么样子的,所以我们希望训练出一个分布,来逼近这个目标
分布。然后从这个分布中 sample 一些点出来,既然能被 sample 出来,而且训练的分布
和目标分布很相似,我们就认为 smaple 出来的图片也符合这样的推断:
符合人的逻辑和审美--》取样出来的--》概率高
不符合人逻辑和审美--》取样出来的--》概率低
>>>>>>>>>
但是,似乎我们并不需要哪些‘不符合人逻辑和审美的’图片,最好就根本 smaple 不出来他们。
所以我们不仅仅是:
训练一个分布逼近目标分布。
通过 D(x) 的取值来引导分布的移动。
我们更希望:
训练一个分布他可以把目标分布的高概率区域更高; 低概率区域更低。
这是一种思想,在 structured perceptron 中也有。
10.2 Evaluation Function - structured perceptron
 在 structured perceptron 算法里面就有这种思想:更新 w 的时候,增加对的,减少错的。但是在整个算法中,穷举所有的 y,找到最好的 y~ 这一步是很麻烦的。
在 structured perceptron 算法里面就有这种思想:更新 w 的时候,增加对的,减少错的。但是在整个算法中,穷举所有的 y,找到最好的 y~ 这一步是很麻烦的。
10.3 How about GAN
原来的视角:D(x)是指定的某个函数,只不过形状会有所变化
 新的视角:F(x) 不指定为任一函数,随圆就方
新的视角:F(x) 不指定为任一函数,随圆就方
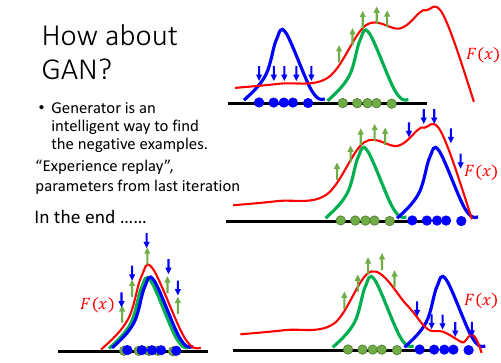
这是另一种 train GAN 的视角:与之前那种固定 D(x)(eg:sigmoid,linear), 然后让 PG 朝 F(x)更大值的地方移动不同。 这里的方法是说:F(x) 不事先假定其为 sigmoid 形状 or linear 形状, F(x) 像是一块布(一个随时变换的函数),凡是 Pdata 范围的点就往上抬,凡是压到 PG 的范围就使劲压,直到 PG 被‘捋’到 Pdata 那里为止,这时候往上抬和往下压的力量相互抵消,
最后 F(x) 和 PG 就都变成和 Pdata 一样的了
所以 F(x) 和 D(x) 有两点不同: -------------------------------------------------------- 1) D(x) 事先指定函数, F(x) 不指定函数 2) D(x) 最后还是这个函数,F(x) 最后会成为和 Pdata 一样形状的函数 3) D(x) 仅仅引导 PG 向 Pdata 移动 F(x) 不仅引导 PG 向 Pdata 移动,而且最后 F(x) = Pdata --------------------------------------------------------
Experience replay: parameters from last iteration 新视角下的 GAN 训练的参数可以复用。
可以复用 —> Energy-based
10.4 Energy-based GAN(EBGAN)
- Viewing the discriminator as an energy function (negative evaluation function)
- Auto-encoder as discriminator (energy function)
- Loss function with margin for discriminator training
- Generate reasonable-looking images from the ImageNet dataset at 256 x 256 pixel resolution without a multiscale approach
这里要统一称呼,原来 GAN 的 discriminator 改为用 F(x), F(x) 取相反数就是 energy-function. 这个叫做能量函数值越小越好。能量函数 = \\x - x~\\, 能量值就是 reconstruction-error
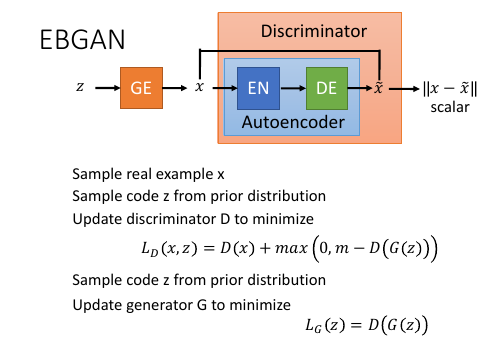 这里生成的图片经过 endocer-decoder 之后还是 image,但是 GAN 要求鉴别器输出的是一个 scalar. 所以就用训练 encoder-decoder NN 的方式,比较 x 和 x~ .
对这个向量取 norm-1 distance. 这实际就是一个 reconstruction error.
这个 \\x-x~\\ = [0,∞], 如果 x 是一个真实图片希望这个值接近 0, 如果是一个生成图片希望这个值越大越好。这一点跟 WGAN 和 GAN 是真好相反的。
这里生成的图片经过 endocer-decoder 之后还是 image,但是 GAN 要求鉴别器输出的是一个 scalar. 所以就用训练 encoder-decoder NN 的方式,比较 x 和 x~ .
对这个向量取 norm-1 distance. 这实际就是一个 reconstruction error.
这个 \\x-x~\\ = [0,∞], 如果 x 是一个真实图片希望这个值接近 0, 如果是一个生成图片希望这个值越大越好。这一点跟 WGAN 和 GAN 是真好相反的。
鉴别器的训练就是要 minimize:
LD(x,z) = D(x) + max(0, m-D(G(z))
m 就是 margin, 事先定好的值,后面会讲到动态 margin
生成器的训练就是要 minimize:
LG(z) = D(G(z))
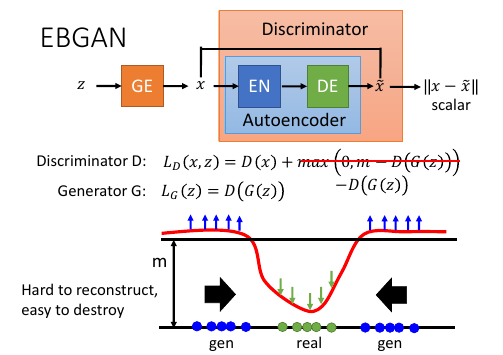 Energy-fn 是 -F(x), 上面 ppt 展示的就是 Energy-fn 的函数图像。
Energy-fn 是 -F(x), 上面 ppt 展示的就是 Energy-fn 的函数图像。
鉴别器训练:
最原始的想法是:让 Pdata 图片的能量函数值越小越好,让 PG 图片的能量越大越好。
但是这样做:对于 autoencoder 是有问题的“hard to reconstruct, easy to destroy”
所以,autoencoder 会倾向于随机搞 PG,也就是 reconsturction error -> ∞
所以,不能让 PG 图片的能量越大越好,而是给一个 threshold:m, 能量一旦超过 m,就把
这个图片的能力置 0. 图片在 m 以下才计算他与 m 的差值作为能量。
一旦大过 m, minimize LD(x,z) = D(x) ,也就是集中对 Pdata 图片的能量进行最小化。
这是合理的。
生成器训练:
生成器训练的目标只有一个,就是希望生成的图片的能量越小越好。
既然 real data 能量小,generated data 就会往 real data
区域靠近。
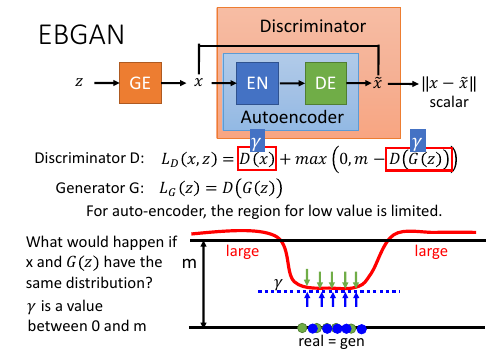 这个式子 LD(x,z) = D(x) + max(0, m-D(x))
当最后结果,PG 与 Pdata 一致了,会出现什么情况呢?假设 D(x) = γ, 所以当γ = 0, LD = m
0< γ < m, LD = γ + m - γ = m
γ = m, LD = m
这个式子 LD(x,z) = D(x) + max(0, m-D(x))
当最后结果,PG 与 Pdata 一致了,会出现什么情况呢?假设 D(x) = γ, 所以当γ = 0, LD = m
0< γ < m, LD = γ + m - γ = m
γ = m, LD = m
>>>>>>>>>>> [qqq]这里几乎没听懂 <<<<<<<<<<<<

Pulling-away term 是希望生成器可以生成多样性较高的图片。
xi --> Encoder -> ei -> Decoder --> xi~
这里取一堆生成图片:S={...xi...xj...}
取各个图片的中间结果:{...ei...ej...}
计算他们两两之间的 cos 相似性:fPT(S) ,希望这个值越低越好,
fPT(S)越低 --> diversity 高
>>> 如何更好的训练这个 auto-encoder for EBGAN ---------------------------------------------------------------- 不但希望,auto-encoder 可以最小化 real image 的 reconstruction-error 还希望,他可以最大化 fake image 的 reconstruction-error, 以此制衡 auto encoder 达到 regular 的效果。 ----------------------------------------------------------------
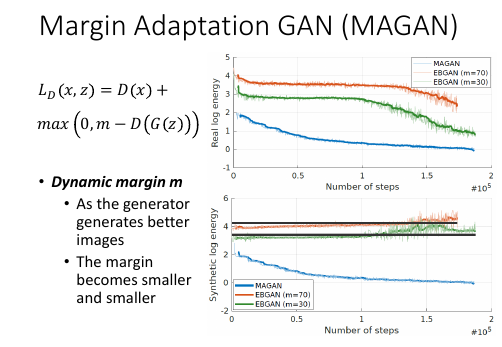
10.5 MAGAN
 EBGAN 中的 LD 中的 m 设置多少合适呢?
EBGAN 中的 LD 中的 m 设置多少合适呢?
只看两张图中 EBGAN 的部分:
ppt 上面是 real data 的 energy
可以看到好像前给个轮数模型的力气都用来让 generated data 的能量上升了
所以 real data 在前几轮并没有发生什么变化,直到后面才开始下降。
ppt 下面是 generated data 的 energy, 其中黑线是 m 的 log 能量值
可以看到,随着轮数进行的越来越多,生成图片的能量值确实会超过 m.
再看 MAGAN 的部分: 两张图中的能量都是在下降,似乎是说,生成器很快就学会如何生成以假乱真的图片了
MAGAN, 动态的 margin Dynamic margin m: As the generator generates better images, the margin becomes smaller and smaller
10.6 LSGAN(Loss-sensitive GAN)
LSGAN 也是一个 adaptive margin
Reference: Guo-Jun Qi, “Loss-Sensitive Generative Adversarial Networks on Lipschitz Densities”, arXiv preprint, 2017
LSGAN allows the generator to focus on improving poor data points that are far apart from real examples. Connecting LSGAN with WGAN
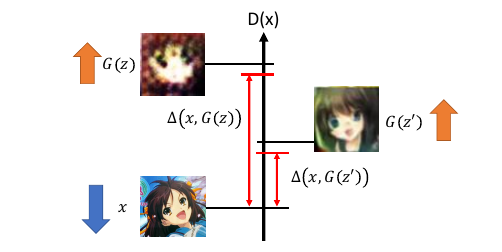
Δ(x,G(z)) 是表示两张图片的差距:具体怎么计算可以用像素间的差距(效果不好),也可以用
train 好的 CNN,把某个 hiden layer 拿出来看两者像不像(效果好)
三张图片:G(z), G(z'), x
x - real image
G(z) - bad generated image
G(z')- good generated image
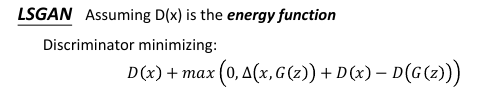
LSGAN 完全可以对比 EBGAN 的 LD 来理解:
EBGAN LD:
LD(x,z) = D(x) + max(0, m-D(G(z)))
LSGAN LD:
LD(x,z) = D(x) + max(0, Δ(x,G(z)) - (D(G(z)) - D(x)))
--------- --------------
m D(G(z))
因为 Δ(x,G(z)) 很高, 这个式子会把 G(z) 顶的高一点;
因为 Δ(x,G(z')) 不高, 这个式子会把 G(z) 顶的低一点;
怎么‘顶’的呢?
D(x) - D(G(z)) > 两个图片之间的差距Δ(x,G(z)), 这个就是 margin
因为两张图片的差距会随着生成器能力不同而产生不同的图片,所以
这个 margin 是一个动态的。
这个 margin 的概念在 structured learning 中也有用到。
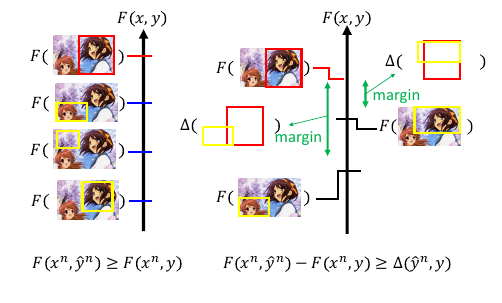
10.7 BEGAN(Boundary Equilibrium GAN)
Ref: David Berthelot, Thomas Schumm, Luke Metz, “BEGAN: Boundary Equilibrium Generative Adversarial Networks”, arXiv preprint, 2017
着他妈产生的人脸也太 tm 好了吧

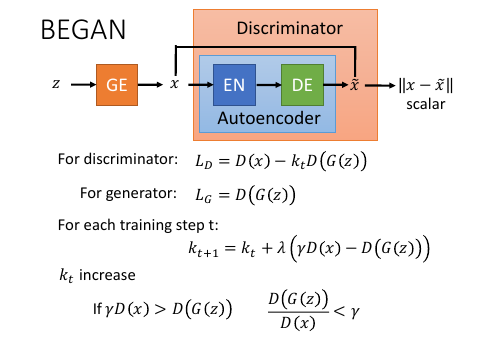
之前说过直接 - D(G(z)) 会有问题,这里是加了一个跟轮数有关的 kt. 一开始 k0 = 0, 也就是说不管 D(G(z)),只让鉴别器把精力放在 最小化 D(x)上 什么时候 kt 开始增加呢?也就是什么时候开始考虑 fake image, 开始考虑把 D(G(z))开始拉高呢? γ 是一个需要自己设置的值; λ 就像 learning-rate 一样是一个正值。 当 D(G(z))/D(x) < γ, 也就是当 D(G(z)) 太小的时候,也就是当 fake image 的 reconstruction-error 太小的时候。

 上面的是机器生成的,下面的是 celebA 的。
上面的是机器生成的,下面的是 celebA 的。


10.8 Ensemble of GAN
10.9 RL and GAN for sentence generation and Chat-bot
作业四 Outline • Policy Gradient • SeqGAN • Two techniques: MCMC, partial • Experiments: SeqGAN and dialogue • Original GAN • MadliGAN • Gumbel
11 Review: Chat-bot
sequence-to-sequence learning
11.1 Chat-bot 基本架构
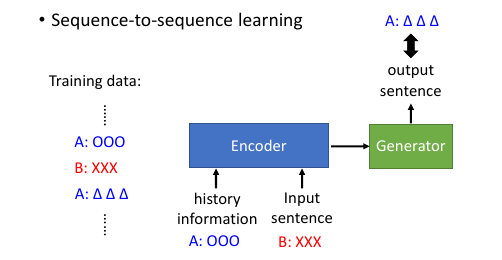 要记得之前的对话,之前说过的句子也要放进 encoder 里面去
要记得之前的对话,之前说过的句子也要放进 encoder 里面去
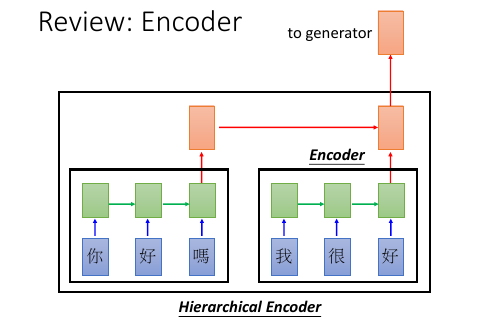 用 RNN 把输入的句子读一遍。
用 RNN 把输入的句子读一遍。
如果你希望还考虑对话者的表情,那么你就可以再接入一个图片信息作为 encoder 的输入。总之,encoder 可以吃各种各样的输入,这取决于你希望 chat-bot 要考虑多复杂的情况。
如果今天 input-information 比较复杂的话,你可能需要一个 hierarchical encoder. 然后你就会有第二阶 encoder(红色方块),他吃比较低阶的 encoder 的输出,然后再做一次 encode.把输出丢给 generator
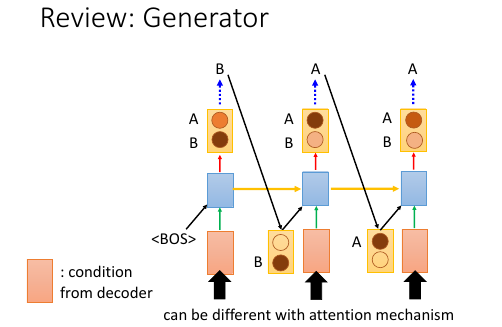 [勘误]左下角应该是 encoder,不是 decoder
[勘误]左下角应该是 encoder,不是 decoder
encoder 给了 generator 一个 vector. 然后 generator 产生一个 word 的分布,表示产生的句子的第一个词汇,除此之外还会给 generator 一个特别的 symbol,代表 begin of sentence.
这里的 generator 一般是一个 RNN.他在第一个 time 输出一个 word distribution. 然后我们从这个 word distribution 里面 sample. eg, sample 的是 word B, 这就是句子的第一个单词。
然后把这个 word B 用 one-hot encoding 编码,然后跟新的 encoder 的输出一起丢到 RNN 在第二个 time 里会产生第二个 word distribution. 然后根据这个 distribution 再 sample 出一个单词。eg, sample 出 word A
如果给 红色的方块 encoder 加入 attention mechanism 的话,encoder 会是不一样的。
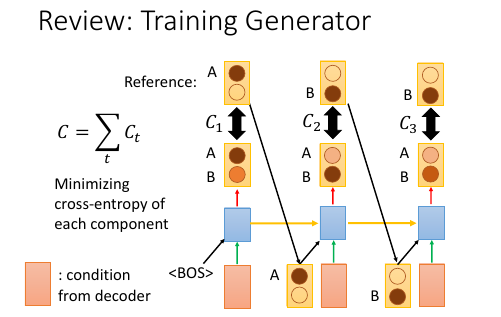
11.2 如何训练 generator 呢?
training 的时候你有标准答案,标准答案会告诉说,现在应该输出什么样的 sentence. 假设 sentence 应该是 ABB.
在第一个 time, model 就会看自己的输出跟 sentence 第一个 word:A 会有多少差异性。差异性:就是算 time-1 输出的分布与目标分布的 cross-entropy:C1
接下来在 training 的时候会把 Reference 丢到下一个 time. 而在 testing 的时候会把 time-1 的输出 丢到下一个 time.
第二个也是一样的过程。
把所有的 C: C1,C2,C3… 统统加起来作为 loss-fn. 调整所有的 encoder 和 generator 的参数来 minimize loss-fn.
11.3 最小化 cross-entropy 就是最大化 likelyhood
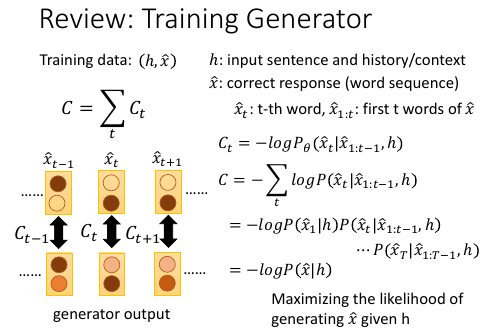
[勘误] -logP(x1|h)P(xt|x1:t-1,h)... 应该是 -logP(x1|h)P(x2|x1:1,h)...
^ ^ ^
就是展开 C 的和式,然后 log 相加变成相乘再 log: loga + logb = log(a*b)
minimize cross-entropy 之和,就是 maximize log likelyhood. 为甚么呢?
假设我们的训练数据是:(h,x^),input h, output should be x^.
h and x^ 都是 sentence.
h 可以是一个句子和一些历史、环境信息(语者的表情等等)
x^1:t, 表示 x^ 这个句子的第 1 到 t 个 word.
t=0 P(h) ---*
t=1 P(x1|h) |-> P(x1,h)--*
t=2 P(x2|x1,h) |-> P(x2,x1,h)--*
t=3 P(x3|x2,x1,h) |-> P(x3,x2,x1,h) = P(x^,h)
但是现在没有 P(h), 他们都是连乘关系,所以去掉 P(h) 后的结果为:P(x^,h)/P(h) = P(x^|h)
C = -ΣlogP(xt|x1:t,h)
= -logP(x^|h)
-------
V
这个公式代表什么呢?
就是如果给定 h,希望输出 x^ 的概率越大越好。所以传统的方法 train 这个模型的方法就是:maximize likelyhood. 下面讲怎么用 RL 来代替 maximum likelyhood 来训练这个模型。
12 RL
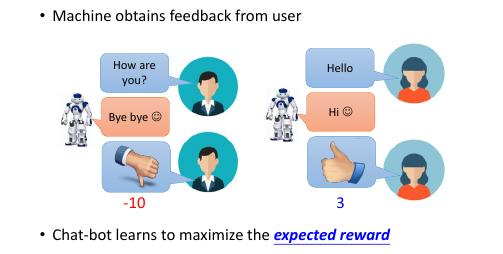
注意 RL 与最大似然的训练样本产生方式不同:最大似然直接使用已有的训练数据 (句子问,句子答):
(h1,x^1) (h2,x^2) (h3,x^3)
这种,通过调整模型参数让這些训练数据的概率在已知(?)的概率分布中是最高的。而 RL 的样本是通过上一代(第一代近乎随机)分布产生,然后觉给人来打分产生的。
(h1,x1) R(h1,x1) (h2,x2) R(h2,x2) (h3,x3) R(h3,x3)
RL 的样本都是这样的。
样本结构不同,产生方式不同,就决定目标函数也不同: ps, 似乎 gradient descent 用来解决 loss-fn 最小化。 ps, 似乎 gradient ascent 用来解决 概率 最大化。两者都是最大化【对的】样本产生的概率,如何知道哪些是【对的】最大似然通过训练集获得,强化学习通过 R(h,x) 函数获得。
所以最大似然的概率最大化目标通过【积分,期望,取样,平均】是:1/NΣlogPθ(x^i|hi) 所以强化学习的概率最大化目标通过【积分,期望,取样,平均】是:1/NΣR(xi,hi)logPθ(xi|hi)
两者的 Gradient 也很相似:
最大似然:1/NΣl∇ogPθ(x^i|hi) 强化学习:1/NΣR(xi,hi)∇logPθ(xi|hi)
最大似然像是【应试教育】,有标准答案强化学习像是【素质教育】,没有标准答案,只有过程中的失败和成功
12.1 Maximizing Expected Reward -1
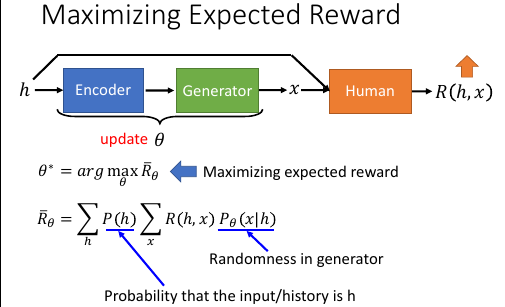 想象出有一个人,他在模型输出之后,会把模型的输入和输出一起拿过来看一看是不是 input 和 outpu 匹配的足够好。人会给这个输入和输出打分:
Reward(h,x)
想象出有一个人,他在模型输出之后,会把模型的输入和输出一起拿过来看一看是不是 input 和 outpu 匹配的足够好。人会给这个输入和输出打分:
Reward(h,x)
机器要做的就是 update θ,使得之后 input 产生新的 output,这个新的 (h,x') 对可以获得 Reward 越高越好。
Expected Reward: R-θ R-θ 的意思是:如果 chat-bot(encoder+generator) 以后都用 θ 这套参数跟人互动,他 期待得到的 Reward 会是多少。
. Rθ = ΣP(h)ΣR(h,x)Pθ(x|h) . ----- . v . 穷举世界上所有可能的输入 h 的概率之和 . . Rθ = ΣP(h)ΣR(h,x)Pθ(x|h) . ------- . v . 所有可能的 Reward,为甚么是所有可能的 Reward 呢? . 因为给固定的 h, 这个 chat-bot 的输出可能是不一样的, . 因为 chat-bot = encoder + generator, . 而 generator 是一个 RNN 他的输出是一个 distribution . 然后 sample 出一个 word, 有一定的随机性。 . 虽然有随机性,但是分布是固定的,怎么固定的呢?通过 h 和 θ。 . / . Rθ = ΣP(h)ΣR(h,x)Pθ(x|h) <-----------------/ . ------- . v . 在给定 h 和 chat-bot 的一套参数 θ 的时候 . chat-bot 输出 x 的几率是多少。 . . Rθ = ΣP(h) ΣR(h,x)Pθ(x|h) . --- ----- ----- . 所以可能的输入 reward 所有可能的输出
下面的事情就是找到一个 θ 来最大化 这个 Rθ
12.2 Maximizing Expected Reward -2
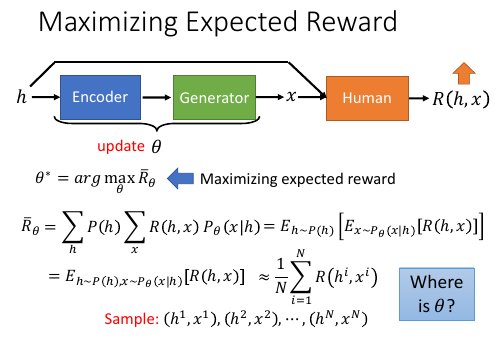
>>> 这里又见到: 积分(和式)-> 期望 -> 取样 -> 平均 但是想要求 θ* = argmax Rθ 需要用 Gradient ascent, 需要求 ∂R/θ
where is θ?
但是这里经过 积分(求和)-》期望-》取样-》平均 这一套近似之后 变量里已经没有 θ 了。 虽然形式上的没有 θ,但其实 θ 是隐藏起来了。 θ 会影响 sample 出来的值。
但我们用 Gradient ascent 是需要形式上的θ的。怎么办?Policy Gradient
12.2.1 引入 policy Gradient,解决没有 θ 问题
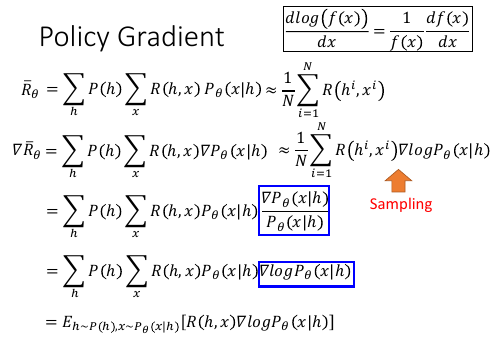
>>> 这里又见到: 积分(和式)-> 期望 -> 取样 -> 平均
[勘误]: ∇Rθ = ΣP(h)ΣR(h,x)∇Pθ(x|h) ≈ 1/NΣR(hi,xi)∇Pθ(xi|hi)
^ ^
前页 ppt 是先用 积分,期望,取样,平均 来近似,然后再求 gradient. 颠倒一下顺序,先求 Grandient 然后 积分,期望,取样,平均
这里 N 是样本个数,i 代表第 i 个样本。
12.2.2 Gradient Ascent
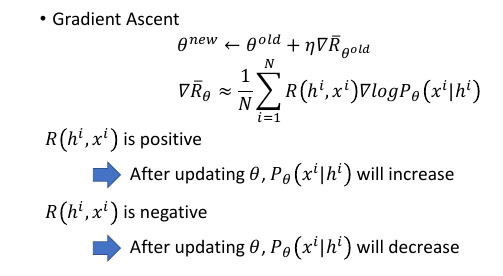 如果某件事情人觉得是对的 R(hi,xi) is positive
那么就应该让这件事情在概率分布中更容易发生:increase Pθ(xi|hi)
反之亦反
如果某件事情人觉得是对的 R(hi,xi) is positive
那么就应该让这件事情在概率分布中更容易发生:increase Pθ(xi|hi)
反之亦反
12.2.3 实做时的问题:对比 likelyhood 和 policy gradient
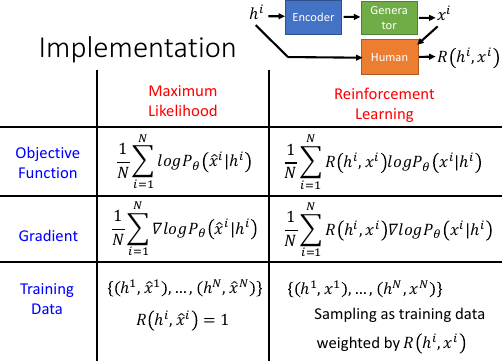
x^i 第 i 个正确的样本 xi 第 i 个样本
最大似然的意思是,让正确的样本的概率最大强化学习的意思是,让正确的样本概率增加,错误的样本概率减小,增加减小通过权重 R(hi,xi)实现
最大似然由于使用【正确的样本】进行训练,所以他相当于已经预知这个样本都是符合【人的要求】的,相当于给每个样本的 R 值都是 1. 而 RL 的训练样本应该是随机样本,判别好坏交给 R(h,x) 函数,然后通过 R 的判别结果作为权重动态的让 正确的样本概率增加,错误的样本概率减少。
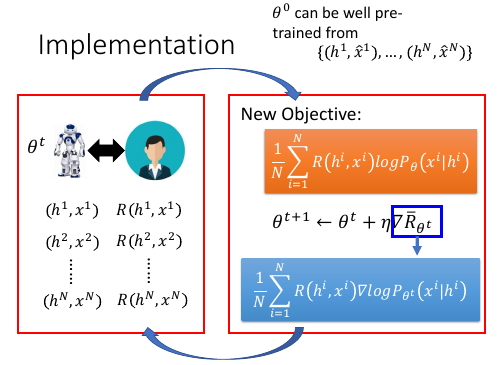 可以这样理解,R(hi,xi) 是多少,就把(hi,xi)复制多少份,这样去 train
[作业二,就是实现 seq-to-seq]
可以这样理解,R(hi,xi) 是多少,就把(hi,xi)复制多少份,这样去 train
[作业二,就是实现 seq-to-seq]
实做初始化的参数 theta 不需要从 random 开始。 可以用最大似然得到 theta0.
12.2.4 Add a Baseline: 纠正 sample 的后遗症
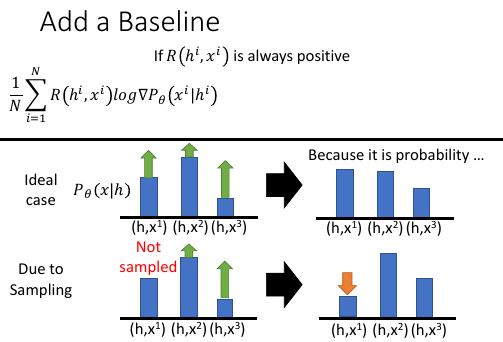
>>> 用 sample 来近似期望和积分的后遗症 当 R 是正值的时候,对应的样本概率应该上升。这是之前 ppt 的结论。 如果使用期望和积分是没有问题的,因为他涵盖了所有样本的情况,每一个 实数点的概率都会根据 R 的不同而调整。
但当我们使用 sample 的时候,就是离散的,有很多点是没有被取样到的。如果这时候取样到的点是正值,這些点的概率会一直上升,可以使用的上升空间还是被认为是‘1’,概率和为 1.這些点会挤占那些没被取样到的点的概率。随着這些 R 值为正的取样到的点概率不断上升,那些没被取样到的点可能 R 值也是正的,但是概率被他人挤占了---這些点概率下降了。
这样得到的分布是肯定不对的。
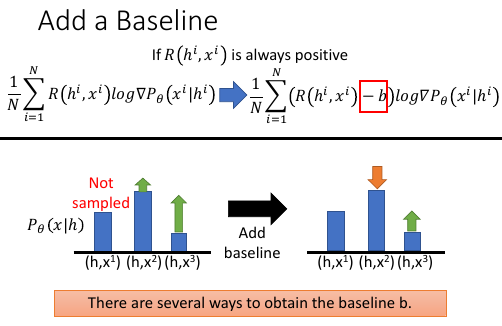 这里提供的方法就是用一个阈值:b,来过滤掉虽然正值但比较小的 reward.
这样做的好处是:相当于整体下调了当前 smaple 到的样本的 reward 之和。只让足够大的 reward 的点上升,让 reward 不够大的点概率下降,这样不会耗尽所有的上升空间。
这里提供的方法就是用一个阈值:b,来过滤掉虽然正值但比较小的 reward.
这样做的好处是:相当于整体下调了当前 smaple 到的样本的 reward 之和。只让足够大的 reward 的点上升,让 reward 不够大的点概率下降,这样不会耗尽所有的上升空间。
[李老师这里要助教来讲如何得到合适的 b,但是没有这部分视频]
12.2.5 Alpha Go style:两个机器交互,R 打分交给函数来做
 刚才的样本结构:
刚才的样本结构:
(h1,x1) R(h1,x1) (h2,x2) R(h2,x2) (h3,x3) R(h3,x3)
这样人需要一直看着,一个个打分,实在太累了。这里采用一种机器与机器互动,打分交给 evaluation function 的方式,类似 alpha go 的学习模式。
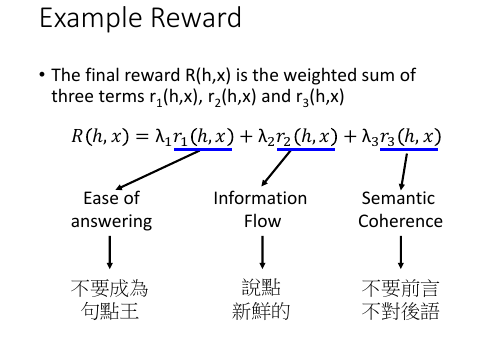 Reward 函数怎么定,是一件比较 tricky 的事情,作业中要求自己定义。这里提供一种方法,把 Reward 拆成幾個小的 rewards, 每一个小 reward
有一个自己的目标,然后权重 lambda 就是你多看重这个小目表。
Reward 函数怎么定,是一件比较 tricky 的事情,作业中要求自己定义。这里提供一种方法,把 Reward 拆成幾個小的 rewards, 每一个小 reward
有一个自己的目标,然后权重 lambda 就是你多看重这个小目表。
 可以比较晚进入死循环的状态!
可以比较晚进入死循环的状态!
还有眾多 policy gradient 之外的技术可以使用,这个请参考 ML 课程中的最后一讲,以及一些论文。
Reinforcement learning? • One can use any advanced RL techniques here. • For example, actor-critic • Dzmitry Bahdanau, Philemon Brakel, Kelvin Xu, Anirudh Goyal, Ryan Lowe, Joelle Pineau, Aaron Courville, Yoshua Bengio. "An Actor-Critic Algorithm for Sequence Prediction." ICLR, 2017.
13 SeqGAN
Lantao Yu, Weinan Zhang, Jun Wang, Yong Yu, “SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient”, AAAI, 2017
Jiwei Li, Will Monroe, Tianlin Shi, Sébastien Jean, Alan Ritter, Dan Jurafsky, “Adversarial Learning for Neural Dialogue Generation”, arXiv preprint, 2017
怎么用 GAN 来训练,sentence generation or chat-bot
13.1 GAN for Sentence Generation
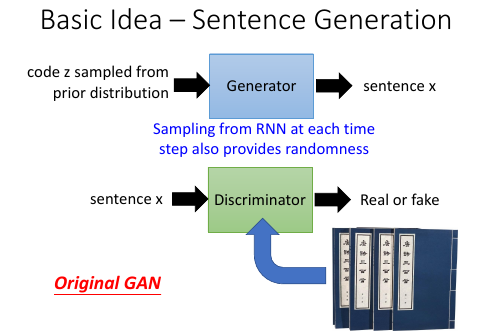 这里依然使用 RNN 作为 Generator。这时候就不需要 code 在这个 normal distribution
来提供·「随机性」, 因为 RNN 的输出本身就是一个 distribution. 他会再从这个 distribution
中 sample 一个点作为 sentence x。
这里依然使用 RNN 作为 Generator。这时候就不需要 code 在这个 normal distribution
来提供·「随机性」, 因为 RNN 的输出本身就是一个 distribution. 他会再从这个 distribution
中 sample 一个点作为 sentence x。
 train 这个 model 需要两个步骤:
train 这个 model 需要两个步骤:
- 训练鉴别器:鉴别器的目标就是让 fake sentence 对应的输出越低越好让 real sentence 对应的输出越高越好。这里的鉴别器可以使用任何的 GAN 来做,普通的 GAN 来是 WGAN 都可以。
- 训练生成器:稍微有点麻烦
[作业三是 conditional GAN]
13.2 GAN for Chat-bot
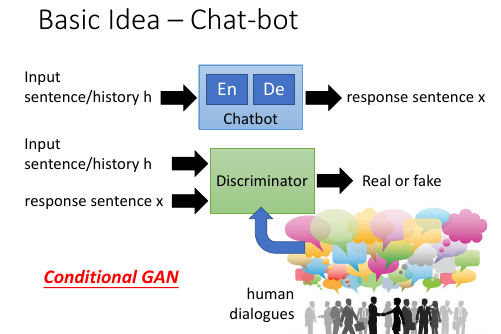 Chat-bot 跟 sentence generation 不同需要使用 conditional GAN
Chat-bot 跟 sentence generation 不同需要使用 conditional GAN
一个 chat-bot 就是一个生成器,然后放在整个 GAN 里面来 train. 目标就是让 chat-bot 产生的句子越来越像人对话。
这里使用 conditional GAN. 鉴别器的输入是两个东西:一个是 chat-bot 的输入,另一个是 chat-bot 的输出,然后通过比对真正的人的对话,来给 chat-bot 输入和 chat-bot 输出的匹配程度打分。
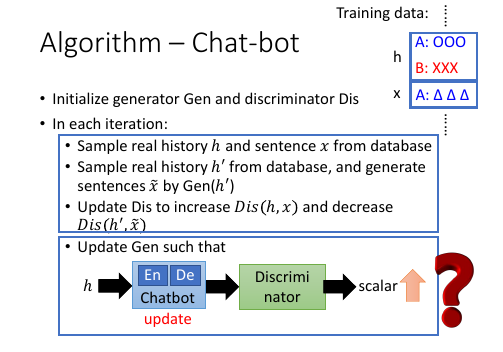
13.2.1 到底生成器的训练会有什么问题呢?
 [注意]GAN 的生成器和鉴别器都可以是 CNN or RNN,GAN 只是一个更大的 generative 框架回忆我们之前怎么训练 GAN 生成器的:固定本代鉴别器参数通过 BP 算法调整生成器参数成为下代生成器,让他生成出本代鉴别器无法分辨的产品。
[注意]GAN 的生成器和鉴别器都可以是 CNN or RNN,GAN 只是一个更大的 generative 框架回忆我们之前怎么训练 GAN 生成器的:固定本代鉴别器参数通过 BP 算法调整生成器参数成为下代生成器,让他生成出本代鉴别器无法分辨的产品。
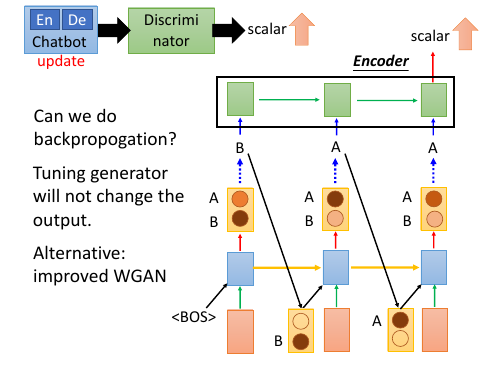
但是这里使用了 RNN 作为生成器的框架之后,RNN 是先输出一个概率分布,然后从这个分布中 smaple 出一个产品作为输出。而鉴别器使用 conditional GAN 框架把上一个鉴别器的输出和本次生成的单词联合考虑给出是否匹配的分数,传给下一个鉴别器。
由于这个过程中 RNN 使用了 smaple.所以我们没办法再通过普通 GAN 所使用的 BP 算法逆传播回去更新生成器的参数---中间的传播过程被 smaple 给隔断了。或者这样理解:生成器 RNN 的参数即使有些需变化,只要最后的 sample 是取概率最大的点作为输出,他整体产生的句子根本不会改变。
这里也许有人会说使用 WGAN,之前也讲过 WGAN 用来实现 seq 的方法。WGAN 没有 sample,而是直接输出一个概率分布,也自然没有产生 单词 BAA, 也自然没有把上一个 time 的单词输出到下一个 time 中这样的过程。
WGAN 和 seqGAN 是两种框架,李老师鼓励学生通过试验分析两种框架的优劣。
13.2.2 seqGAN 改用 RL 训练生成器
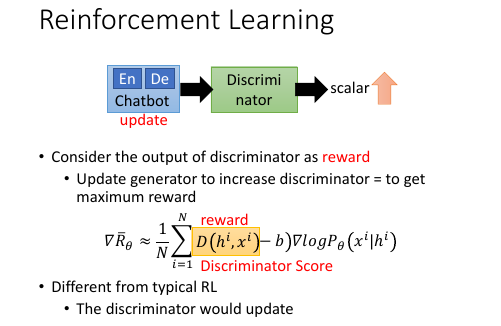 之前讲解 RL 下的 chat-bot 的时候,使用类似这样的数据点:
之前讲解 RL 下的 chat-bot 的时候,使用类似这样的数据点:
(h1,x1) R(h1,x1) (h2,x2) R(h2,x2) (h3,x3) R(h3,x3)
使用这样的数据点可以替换掉以前使用最大似然的方法的数据点:
(h1,x^1) (h2,x^2) (h3,x^3)
目标函数和 Gradient ascent 函数都发生改变。
使用 RL 的 reward 来作为鉴别器,R(hi,xi) 就变成 D(hi,xi) D(hi,xi) 就是鉴别器的输出,我们也是要通过 Gradient Aascent 最大化这个通过【积分-期望-样本-平均】 获取的目标函数。
13.2.3 g-step and d-step
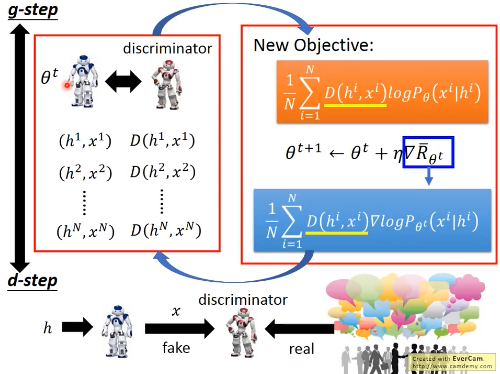
然后整个过程就变成,g-step 和 d-step 交替进行: g-step: 训练生成器 从 θt sample 出一堆 data (hi,xi),然后交给鉴别器取打分 D(hi,xi) 通过新的 target-fn 和 新的 gradient 利用 Gradient ascent 方法 更新 θt --> θt+1 d-step: 训练鉴别器(人) 给‘人’一堆真假数据,让他学习如何分辨他们,并给他们打分。
14 how to improve seqGAN
 这里大概介绍了为什么(概率模型包含生成模型和判别模型)生成模型需要大量数据:因为某一部分的概率确实可以通过其他部分来补足修正。
这里大概介绍了为什么(概率模型包含生成模型和判别模型)生成模型需要大量数据:因为某一部分的概率确实可以通过其他部分来补足修正。
【地图炮】,一棒子打死一堆人。 . 比如这里 hi = what is your name, xi = i dont know . 很显然这是一个不好的匹配,xi 这个回答容易让对话过早结束,不符合人们对话的日常习惯。 . 所以 D(hi,xi)-b 肯定是负值,然后这会让 logP(xi|hi) 下调自己的概率。 . . 回忆之前的模型,xi 这个句子是通过每一个 time 产生一个 word 组合而成: . logP(xi|hi) = logP(xi1|hi) + logP(xi2|hi,xi1) + logP(xi3|hi,xi1,xi2) . 当使用 RL as generator 时,整体下调这个句子的概率就有可能下条每个 time 上产生各自 . 单词的概率: . 【地图炮】,一棒子打死一堆人。 . . 比如同时下调 ‘I’ 'dont' 'know' 三个单词的概率,但是第一个单词是被【误伤】的。 . I 开头没有必要下调:what is your name, I'm John 如果数据量很大就可以相互补充: . 如果数据量很大,有各种各样的句子(比如很多 I 开头的句子), . I 被【误伤】就可以在另一对样本中被【疗养】 但是如果数据量不大,概怎么办呢? . 可以细化到【给所有之前的单词给一个 reward】,这样可以控制每一个单词的概率增减
14.1 Method1: Reward for Every Generation Step

T 表示经过 T 个 time,每个 time 输出一个单词,总计 T 个单词。
Q(hi,xi1,xi2,...) 对比原式理解 R = Σ(R(xi,hi)-b)logP(xi|hi)
R = Σ{(Q(x1,h1)-b)logP(x1|h1)+
(Q(x2,x1,h1)-b)logP(x2|h1,x1)+
(Q(x3,x2,x1,h1)-b)logP(x3|h1,x1,x2)
.
. /-----------------------\
. h -->chatbot--> x1 -->R(x1,h)
.
. /-----------------------\
.x1,h -->chatbot--> x2 -->R(x2,x1,h)
[对 RL 的 seq generation 理解不够]
这样就可以理解 Q 为甚么是这个样子了?然后如何计算 Q: 1. 蒙特卡洛搜寻算法 2. DFPDS
14.1.1 Method1:MC for Q(hi,xi1,xi2…)

利用生成器,但是固定第一个单词是 'I',然后让他生成各种各样的句子,把這些句子都交给 D(hi,x) 来打分,然后把所有分数取平均就是 Q(hi,'I') 的值
14.1.2 Method2:DFPDS for Q(hi,xi1,xi2…)

训练一个可以吃进‘句子一部分’并给出分数的鉴别器。普通的鉴别器是 h(what is your name) + x(i am john) —> 鉴别器 –> scalar 现在训练的鉴别器要能吃进 I am 和 I 并且也输出 positive scalar. 这就是 Q(h,x1:t)
>>>>>>>>>>>>[qqq] 这里没听懂 <<<<<<<<<<<<<<
14.2 Method2: Teacher Forcing

从训练数据中抽出一部分作为 seqGAN 的训练数据,之前 seqGAN 的训练数据是从分布中直接 sample 出来的,没有利用這些已知的数据。
>>>>>>>>>>>>[qqq] 这里没听懂 <<<<<<<<<<<<<<
14.3 如何衡量生成的句子的好坏:Synthetic Data
 对话质量是一件很主观的事情,怎么衡量对话质量的好坏呢?
对话质量是一件很主观的事情,怎么衡量对话质量的好坏呢?
把 seqGAN 先当作一个学生,用一个很容易比对好坏的模型 LSTM 去生成一些 data 用他来作为数据,喂给 seqGAN 看 seqGAN 的【学习能力】如何,看他能不能学到 LSTM 这个生成模型的概率分布。
然后让 LSTM 计算所有 seqGAN 生成的句子的 NLL,越 small 越 better.
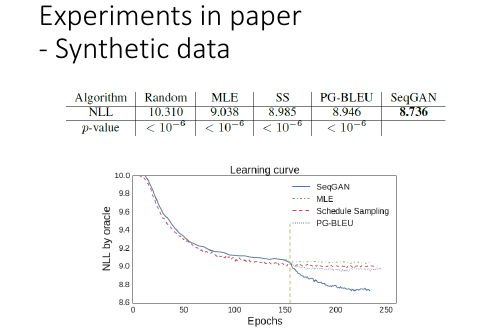
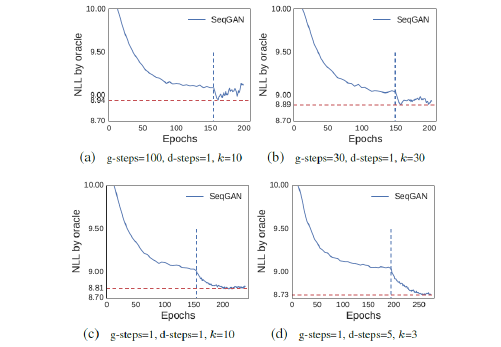
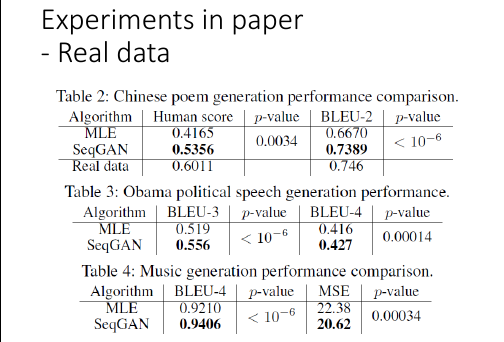 MLE = maximum likelyhood
MLE = maximum likelyhood
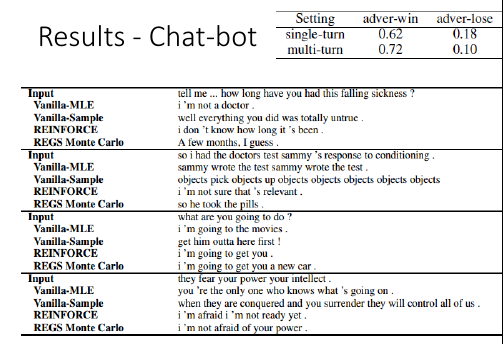

To learn more …… • Professor forcing • Alex Lamb, Anirudh Goyal, Ying Zhang, Saizheng Zhang, Aaron Courville, Yoshua Bengio, “Professor Forcing: A New Algorithm for Training Recurrent Networks”, NIPS, 2016 • Handling discrete output by methods other than policy gradient • MaliGAN, Boundary-seeking GAN • Yizhe Zhang, Zhe Gan, Lawrence Carin, “Generating Text via Adversarial Training”, Workshop on Adversarial Training, NIPS, 2016 • Matt J. Kusner, José Miguel Hernández-Lobato, “GANS for Sequences of Discrete Elements with the Gumbel- softmax Distribution”, arXiv preprint, 2016
14.4 Evaluation of GAN
(and other generative models)
• Lucas Theis, Aäron van den Oord, Matthias Bethge, “A note on the evaluation of generative models”, arXiv preprint, 2015 这篇 paper 不是针对 GAN 写的,而是针对所有的 Generative model 生成模型所以具有普适性
14.4.1 通过混合高斯的 likelyhood 来评断
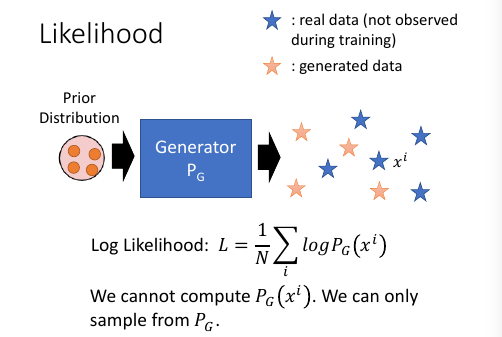 一般情况下,我们如何衡量生成模型的好坏呢?训练的时候会拿出【一部分训练集数据】训练,训练完之后,拿另一部分数据,用这个生成模型求每一个数据点的产生概率,然后算出 log likelyhood 越大越好。 这种验证方法适用于生成模型是一个固定公式的情况,比如高斯混合模型。
一般情况下,我们如何衡量生成模型的好坏呢?训练的时候会拿出【一部分训练集数据】训练,训练完之后,拿另一部分数据,用这个生成模型求每一个数据点的产生概率,然后算出 log likelyhood 越大越好。 这种验证方法适用于生成模型是一个固定公式的情况,比如高斯混合模型。
但是这种方法没法用在 GAN 上,因为 GAN 不会形成一个固定公式,无法计算 PG(xi).自然也就无法使用 log likelyhood 的值来衡量模型好坏,GAN 只能做 sample,他从一个 Prior distribution 中 sample 一些点经过自己的转换之后生成另一些点。
GAN 只会做这个,也只能通过这种方法来提供一些【随机性】,但是这样的生成模型如何衡量好坏呢?
 虽然不知道这个 Generator 的概率公式,但是我可以用一个【有概率公式】的分布来模拟这个 Generator 的概率分布:a model has formula ≈ Generator
常用的方法是:用一个混合高思模型来逼近 GAN ,从 prior distribution 生成的点经过 GAN 之后产生的点,假设每一个点都是一个高斯分布产生的,为了简化计算假设所有高斯的协方差矩阵都一样,计算所有点的 mean,作为混合高斯的 μ。
虽然不知道这个 Generator 的概率公式,但是我可以用一个【有概率公式】的分布来模拟这个 Generator 的概率分布:a model has formula ≈ Generator
常用的方法是:用一个混合高思模型来逼近 GAN ,从 prior distribution 生成的点经过 GAN 之后产生的点,假设每一个点都是一个高斯分布产生的,为了简化计算假设所有高斯的协方差矩阵都一样,计算所有点的 mean,作为混合高斯的 μ。
这样得到一个最【像 GAN】的混合高斯模型,再从训练集中拿出一部分点,通过混合高斯模型的公式计算每一个点的 log likelyhood 值,他们的和越大越好。
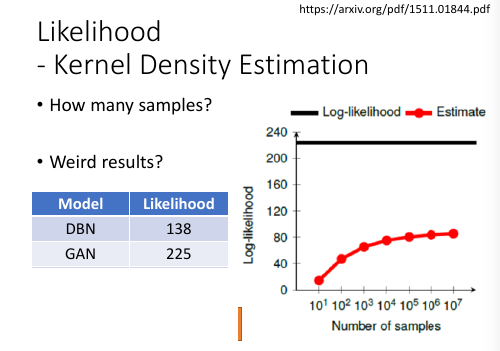 但是我需要 GAN 生成多少个点,来求取一个能近似 GAN 的高斯混合模型呢?试验表明这件事情很 weird. 总是没有一个有说服性的说法。
但是我需要 GAN 生成多少个点,来求取一个能近似 GAN 的高斯混合模型呢?试验表明这件事情很 weird. 总是没有一个有说服性的说法。
 另外一边,Likelyhood 真的能代表 quality 么?比如有一个 GAN 产生了一堆 diversity 很小的图片,但是图片质量非常高。比如都是春日。然后我找一个能最像这个 GAN 的混合高斯模型,然后再用样本集中的数据带入这个混合高斯模型的公式去计算 likelyhood,但是由于样本集中可能只有很少的春日。但是这个高斯模型是根据只产生春日的 GAN 逼近出来的。所以这个 likelyhood 肯定是非常小的。这就矛盾了:图像质量很高的 GAN
通过这种高斯混合近似得出的 likelyhood 却很小。
另外一边,Likelyhood 真的能代表 quality 么?比如有一个 GAN 产生了一堆 diversity 很小的图片,但是图片质量非常高。比如都是春日。然后我找一个能最像这个 GAN 的混合高斯模型,然后再用样本集中的数据带入这个混合高斯模型的公式去计算 likelyhood,但是由于样本集中可能只有很少的春日。但是这个高斯模型是根据只产生春日的 GAN 逼近出来的。所以这个 likelyhood 肯定是非常小的。这就矛盾了:图像质量很高的 GAN
通过这种高斯混合近似得出的 likelyhood 却很小。
另外,如果有一个 GAN 很好的产生图片而且通过高斯混合估计出的 likelyhood 也很高,假设还有一个 GAN 他只有前一个 GAN 1% 的产生能力,基于这种假设算一下两者 likelyhood 值差距却只有 4.6 ,4.6 根本没什么差距。 这也很蛋疼:质量相差很大,likelyhood 却相差很小。
这一切都指向一个问题:也许用高斯混合的 likelyhood 去估计 GAN 是不准确的。
14.4.2 通过 well-trained CNN 来评断
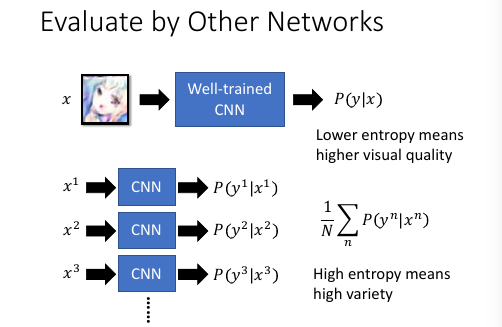
如果不能使用高斯混合的 likelyhood 来估计 GAN 的质量,还有什么方法呢?
可以通过一个【已经训练好的分类器 CNN】,CNN 的输出是一个 P(y|x),对于 6 分类问题大概是这样子:
. _ _ . / 0.1 / . / 0.1 / . x -> CNN -> / 0.7 / 每一个位置都代表 x 属于这个 分类 i 的概率 . / 0.05/ . / 0.05/ . / 0 / . - -
CNN 衡量图片质量: 如果 GAN 生成的图片,经过 CNN 分类器输出的结果是【某一位很突出】的说明 CNN可以 很好的判别图片是什么,也就是说图片质量比较好;如果 CNN 输出的结果【每一位都很 平均】说明 CNN 分辨不出这个图片是什么,说明图片质量不好。怎么计算这件事情,就 是把 CNN 输出的概率向量,用 cross-entropy 计算,cross-entropy用来衡量这各向量 各个值的分散程度,所以 cross-entropy 越小越好。 CNN 衡量图片差异性:diversity 把 GAN 生成的一堆图片都放到 CNN 分类器中,把所有输出的概率向量相加取平均得到的 还是一个向量,然后计算这个向量的 cross-entropy,如果值越大越说明 GAN 生成的图片 diversity 很好。 这是衡量 GAN 的两个维度:quality and diversity. 两个都要算,才能决定 GAN 的好坏。
 这篇 paper 把上述 CNN 衡量 GAN 的方法整合起来,并且给出了公式:
这篇 paper 把上述 CNN 衡量 GAN 的方法整合起来,并且给出了公式:
这个公式化简之后,可以得到一个 Negative entropy 和一个 cross entropy.
这个 negative entropy 就是 P(y|x) 自己跟自己的 cross entropy 的负值,对应上页 ppt 的【质量衡量】,我们希望 cross entropy 越小越好,也就是Negative entropy 越大越好。这个 cross entropy 是 P(y|x) 和 P(y) 的 cross entropy, 对应【差异性衡量】希望这个值越大越好。
所以两个都是越大越好,所以希望这个公式(inception score) 也是越大越好。
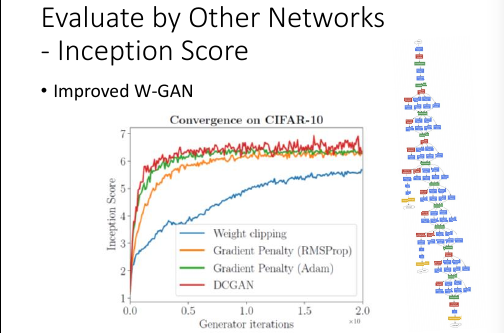 用 inception score 来衡量各种 GAN
用 inception score 来衡量各种 GAN
14.4.3 判断 GAN 是否有创新是很难的
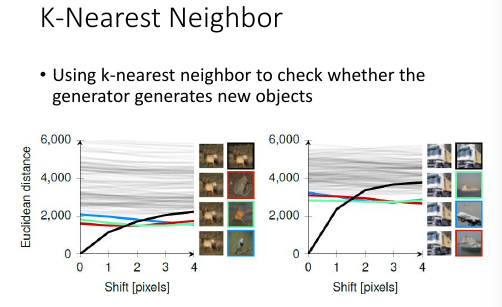
14.4.4 missing mode 有办法衡量
 有 mode callapse
因为你没办法看完所有的 dataset,所以你也就没法知道哪些部分没有生成。
有 mode callapse
因为你没办法看完所有的 dataset,所以你也就没法知道哪些部分没有生成。
怎么知道哪些 mode 被 misssing 了呢? learn 一个 鉴别器,input 生成器的图片 和 database 的图片,然后看哪些图片被超高概率的认为是真的。
>>>>>>>>>>>> [qqq] 没听懂 <<<<<<<<<<<<<<<<<<<
14.5 Application of GAN
14.5.1 Video Generation by GAN
Michael Mathieu, Camille Couprie, Yann LeCun, Deep multi- scale video prediction beyond mean square error, ICLR, 2016 Pac-Man: https://github.com/dyelax/Adversarial_Video_Generation UCF101: http://cs.nyu.edu/~mathieu/iclr2016extra.html
14.5.2 Image super resolution by GAN
• Image super resolution • Christian Ledig, Lucas Theis, Ferenc Huszar, Jose Caballero, Andrew Cunningham, Alejandro Acosta, Andrew Aitken, Alykhan Tejani, Johannes Totz, Zehan Wang, Wenzhe Shi, “Photo-Realistic Single Image Super- Resolution Using a Generative Adversarial Network”, CVPR, 2016
14.5.3 Speech Synthesis
• Speech synthesis • Takuhiro Kaneko, Hirokazu Kameoka, Nobukatsu Hojo, Yusuke Ijima, Kaoru Hiramatsu, Kunio Kashino, “Generative Adversarial Network-based Postfiltering for Statistical Parametric Speech Synthesis”, ICASSP 2017 • Yuki Saito, Shinnosuke Takamichi, and Hiroshi Saruwatari, "Training algorithm to deceive anti-spoofing verification for DNN-based speech synthesis, ”, ICASSP 2017
