UP | HOME

lec-23 Structured Support Vector Machine

Table of Contents

1 Structured Support Vector Machine

1.1 上节课回忆

重新梳理 Structure Learning 相关概念 Unified Framework

Training Inference(Testing)
Find a function F: Find a y~ :
F: X * Y -> R Given an object x
evaluate how compatible the y~ = arg maxF(x,y)
objects x and y is  

虽然看起来这个 Framework 很简单，但是你需要回答【神之三问】：

Problem1:Evaluation what does F(x,y) look like?
Problem2:Inference How to solve the "arg max" problem
Problem3:Training Given training data, how to find F(x,y)

Example Task: Object Detection ============================ 在影像处理领域还有很多比 bounding-box 更复杂的问题，比如【描边】【动作】

screenshot_2017-06-17_20-26-44.png

Problem 1: Evaluation, φ 

这一步需要解决：φ

上节课已经说了，如果能对 F(x,y) 做一些假设，能让我们的任务变的容易一些。 ===> F(x,y) is linear

x an image
y box
(x,y) boxed-image
φ(x,y) features of boxed-image
F(x,y) compatible of box and iamge

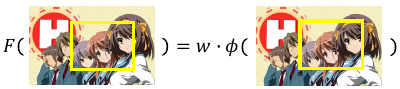
screenshot_2017-06-17_20-50-02.png

what if F(x,y) is not linear? 这方面的研究还很少，大部分都需要这个假设，否则很多推导都不成立了。所以 F(x,y) = W•φ(x,y) 依然是我们所有讨论的根据。所以 Problem 1 的核心问题还是 feature extraction 得到 φ

Problem 2: Inference, y~ 

这一步需要解决：y~

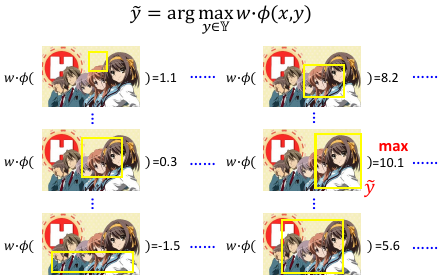screenshot_2017-06-17_20-54-47.png 至于该怎么穷举，这个需要自己想出另一种算法来解决这个问题，可以效率的解决。这里是传统算法的领域。

  • Object Detection • Branch and Bound algorithm • Selective Search
  • Sequence Labeling • Viterbi Algorithm
  • The algorithms can depend on φ(x,y) 以上所有這些算法都依赖 φ(x,y), 不同的 φ(x,y) 就需要不同的算法换言之，這些算法【不普适】
  • Genetic Algorithm 基因算法是可以【普适】，但是找出的解不够精准
  • Open question: • What happens if the inference is non exact? 如果‘从无限多个 y 中找出一个可以让分数最大的’ 这件事是做不到的，该怎么办呢？这件事情影像有多大呢？这件事情也是学界研究很少的领域

所以根据已上所说，我们暂时只能假设 problem 2 已经解决，至于解决方法，case to case.

Problem 3: Training, W 

这一步需要解决：W

screenshot_2017-06-17_21-09-37.png

1.2 Outline

下面的讨论，暂时忽略 problem 1 and 2, 集中精力解决 problem 3.

  1. Separable case
  2. Non-separable case
  3. Considering Errors
  4. Regularization
  5. Structured SVM
  6. Cutting Plane Algorithm for Structured SVM
  7. Multi-class and binary SVM
  8. Beyond Structured SVM (open question)

1.3 Separable case

假设映射到 W 上之后的【最大分数点】与【其他分数点】是可以分开的这件事情用数学表达式和图像表示如下：

screenshot_2017-06-17_21-17-15.png

有了这个假设之后，我们就可以使用【Structured perceptron 算法】来找到 problem3 的核心问题：W

screenshot_2017-06-17_21-19-25.png

1.3.1 算法更新次数的数学推导

先给结论：只需要最多更新 W 【(R/δ)的平方次】，就可以得到最终 W

screenshot_2017-06-17_21-21-51.png

screenshot_2017-06-17_21-27-52.png

screenshot_2017-06-17_21-29-02.png

screenshot_2017-06-17_21-30-50.png

screenshot_2017-06-17_21-32-41.png

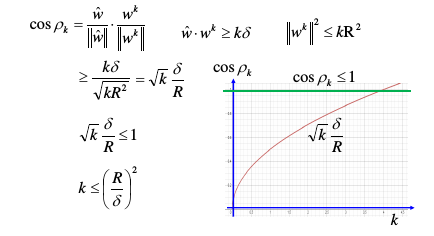
screenshot_2017-06-17_21-33-50.png

1.3.2 How to make training fast

单纯的倍化 δ 比如 –> 2*δ 并不会让算法更快，因为这也会让 R–> 2*R

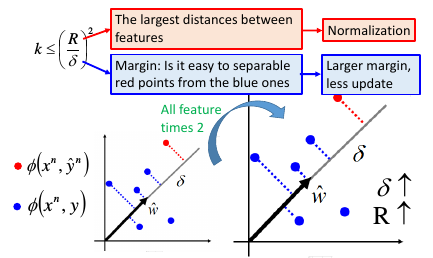
screenshot_2017-06-17_21-41-36.png

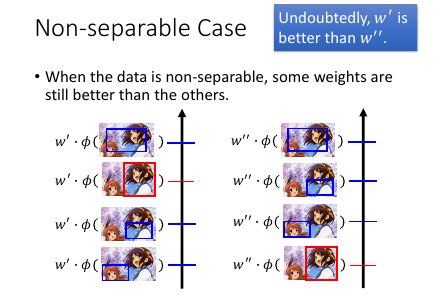
1.4 Non-separable case

如果没有一个 w 可以把 φ(x,框对) 和 φ(x,瞎吊框) 分开我们依然可以衡量哪些 w 更好－－－ 

让 φ(x,框对) 的分数（W•φ(x,框对)) 更高的 w 是更好的 w

screenshot_2017-06-17_21-47-22.png

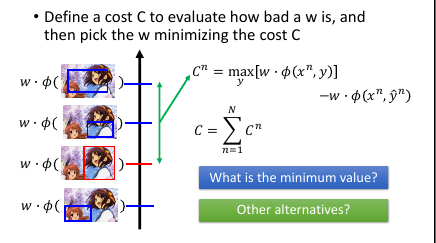
1.4.1 Defining Cost Function

定义 cost-fn 来衡量一个 w 的好坏： cn = 第 n 个 image, φ(xn,所有框法)最高的分数 - φ(xn,框对)的分数 cn = max[w.φ(xn,y)] - w.φ(xn,y~n) C = c1 + c2 + c3 … + cN (假设总共 N 个图片) 为甚么使用 max[w.φ(xn,y)] ,而不是其他方法？因为这是 problem 2 给出的答案，而我们之前假设 problem 2 已经解决所以 max[w.φ(xn,y)] 是‘已知’的。就不用再额外制造问题了。

screenshot_2017-06-17_21-57-13.png

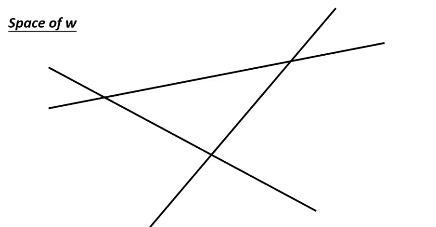
1.4.2 SGD

screenshot_2017-06-17_22-00-41.png

因为 W 是一个 vector, 假设说 w 是二维度的，那么所有可能的 w 就组成一个平面，这个平面被 max 切割成好几块，如果某一个 w 落在中间那块，那么得到的最大分数就是 y'' 贡献的，如果 w 落在左下角那块，那么得到的最大分数就是 y' 贡献的。

相当于用贡献最大分数的 y' y'' y'''… 来给不同的 w 分组。

在每一个 region 里面他的 max-fn 是可以非常轻易的算出来的－－－直接就可以去掉 max 符号。 在边界上是没法微分的，但在 region 内部对 w 微分是很简单的。

screenshot_2017-06-17_22-28-27.png

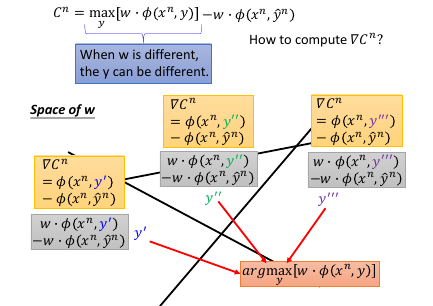
screenshot_2017-06-17_22-01-05.png

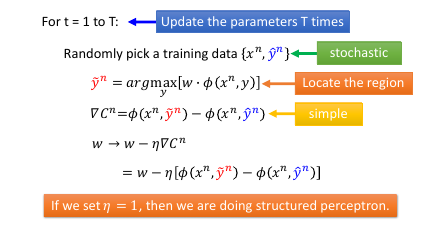
screenshot_2017-06-17_22-54-30.png

1.5 Considering Errors

φ(x,瞎吊框) 之中也有好跟不好的：按照他离 φ(x,框对) 的 相似度 来区分优劣

如果没有一个 w 可以把 φ(x,框对) 和 φ(x,瞎吊框) 分开我们依然可以衡量哪些 w 更好－－－ 

让 φ(x,框对) 的分数（W•φ(x,框对)) 更高的 w 是更好的 w

现在对 w 的期望更高： w 应该给与的功能是【像是一种排序】 

w 应该让越像框对的分数越高，越不像的分数越低。

这样做还可以给整个 model 带来更高的稳定性！

>>> SVM 感觉初现

回忆 SVM 的感觉：不但分的对，还要分的好。 SVM 的 loss-yf 图像可以看到，当 y 和 f 同号但是 yf 乘积 < 1 也就是 f 比较小的时候，这时候 loss 仍然不是最小值，只有当 yf >=1 的时候才是最优结果所以 SVM 有让 f 在与 y 同号的基础上绝对值越大越好的倾向 — margin 越大越好

这里也是一样，不但要把【框对】和【瞎吊框】 分开，还要对 [瞎吊框]分级

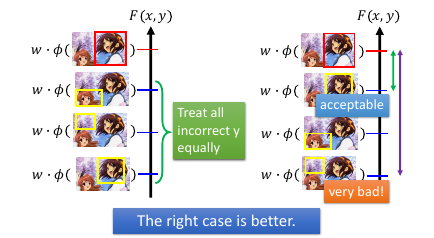
screenshot_2017-06-17_23-00-05.png

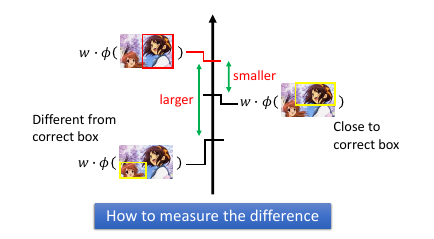
screenshot_2017-06-17_23-01-07.png

如何定义相似度？

1.5.1 Define Error Function

一件 task-dependent 定义:这里使用面积来定义 

Δ = 1 - 相交面积/相并面积
像我的---> 0 <= Δ <= 1 <---- 不像我的

w.φ 是用来衡量【框和图】之间是否匹配：选皇帝Δ 是用来衡量【框和框】之间是否匹配：皇帝带上亲属 w.φ 的意思就是（不管像谁）让框的最好的往前排，其他无所谓Δ 的意思就是（不管分数）让像我的往前排，不像我的往后排

>>> 相似性 similarity

相似性到目前为止： 

两个向量是否相似：inner-product
两个分布是否相似：cross entropy
自己跟自己是否相似：how concentrate(cross entropy)
两个分布的距离是否相近：KL divergence(公式与 cross entropy 有点像)
===> 两个 box 的相似度：Δ = 1 - 相交面积/相并面积

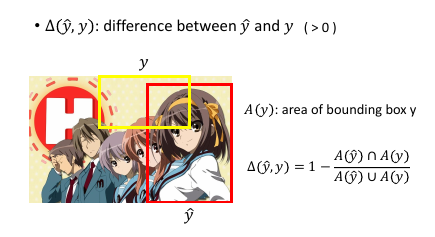
screenshot_2017-06-17_23-08-05.png

1.5.2 Another Cost Function

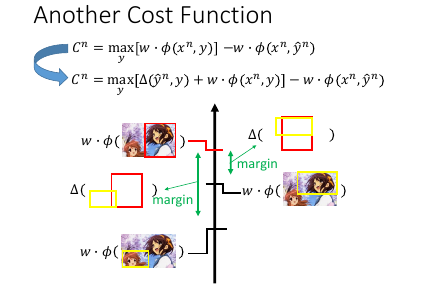screenshot_2017-06-17_23-08-54.png 什么时候 Cn 会最小呢？

  1. 【框对的】分数要比其他【瞎吊框】的分数要高
  2. 而且要高出一个 error-fn 所形成的 Δ 值

满足这两个条件，Cn 才会最小。

>>> 改变的 problem 2

这样,Problem 2 的计算要改变了： max(所有框的分数) =======> max(与皇帝相似度 + 所有框的分数)

所以 Δ 的定义要谨慎，他容易让 problem 2 的计算变复杂

1.5.3 Gradient Descent

screenshot_2017-06-18_10-14-20.png

1.5.4 Another viewpoint

screenshot_2017-06-18_10-18-56.png 一种妥协，通过 minimize C 找到的 w 未必 minizie C', 但也不会让他很大。

这里证明为甚么是 upbound 方法 1: margin rescaling

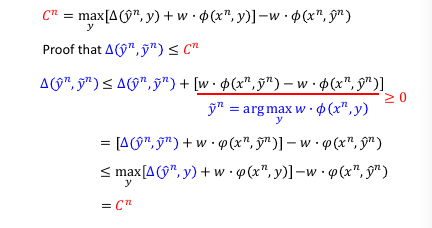
screenshot_2017-06-18_10-21-40.png

方法 2: slack variable rescaling

screenshot_2017-06-18_10-24-33.png

1.6 Regularization

Training data and testing data can have different distribution. w close to zero can minimize the influence of mismatch. Keep the incorrect answer from a margin depending on errors

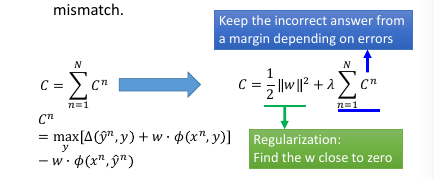
screenshot_2017-06-18_10-29-20.png

screenshot_2017-06-18_10-31-06.png

1.7 Structured SVM

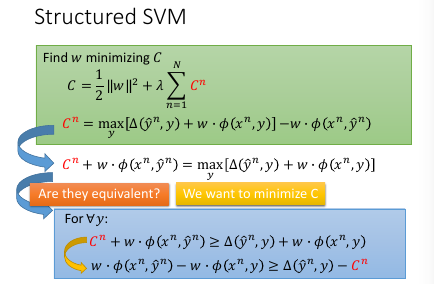screenshot_2017-06-18_10-33-28.png >>> 又见 max 不一样

  1. cn + w•φ = max
  2. cn + w•φ > ∀y

这两件事情是【完全不一样】的，千萬注意 max 带给你的迷惑二式 是没有上界的一式 是 有上界的

>>> 又见 minimize 约束 >

刚才说明了 max ≠ >∀但是这里是 'Find w minimizing C' 用 minimize 规定了一个 tight upbound max = minimize(>∀)

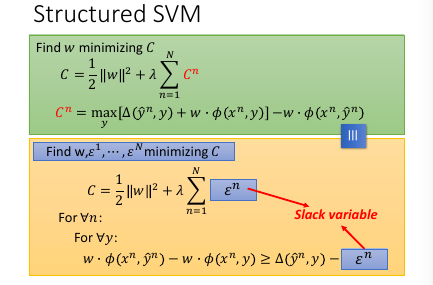screenshot_2017-06-18_10-46-31.png cn -> slack variable

screenshot_2017-06-18_10-48-44.png

1.7.1 Slack variabel(亢龙有悔)

放宽对 w 的限制，防止找不到需要同时满足这么多条件的 w

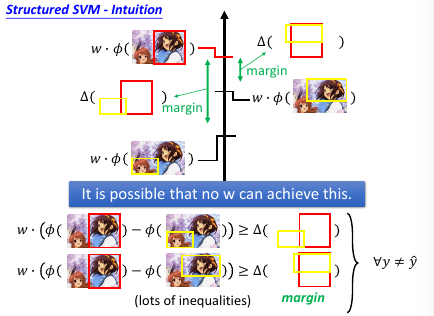
screenshot_2017-06-18_10-50-57.png

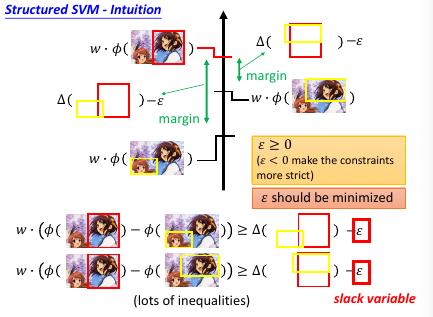screenshot_2017-06-18_11-28-52.png ε 的作用是放宽对 w 的限制，所以叫做 slack variable

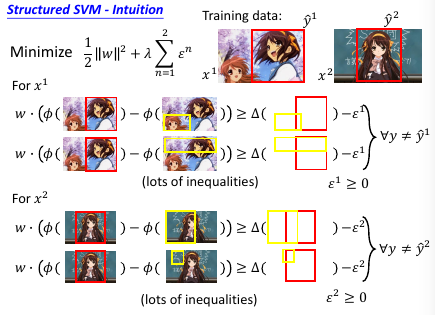
screenshot_2017-06-18_11-33-34.png

总结变化：一开始是要求 w 可以让 框对 分数最高然后变成 w 可以让 框对 分数越高越好然后变成 w [不但]可以让 框对 分数越高越好，还可以让 像框对 的分数更高亢龙有悔 也不同那么较真，给一个放宽条件

screenshot_2017-06-18_11-40-59.png 条件太多了，我们怎么办？

1.8 Cutting Plane Algorithm for Structured SVM

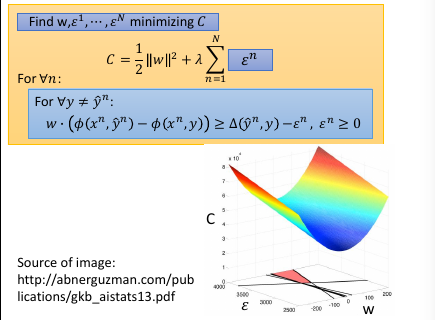screenshot_2017-06-18_11-51-06.png 如果不看 constrain, 那么 w=0,ε＝0 就可以得到 minimization C 可以根据这个 C = 1/2w2 + ε 画出函数图像，

再来看 constraint: data 都是已知的每一个 data 进来都会构造一个关于 w 和 ε 的线性表达式，也就在 w 和 ε 坐标系中画了一条线，因为 constraint 都是不等式，这条线就规定了 w 和 ε 只能在线的一边取值。有多少 y 就有多少 constraint ,也就有多少条线。他们共同在 w 和 ε 平面分割出一个空间，w 和 ε 只能在这个空间中取值。

screenshot_2017-06-18_12-04-41.pngh

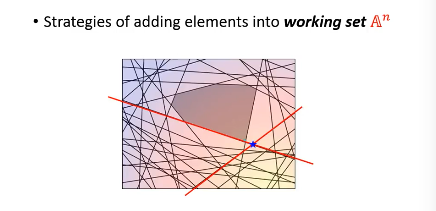
虽然线条很多，但真正起作用的线条就那几条，比如下图中红色的线条是需要的，而绿色可以删掉不看。从这个角度想，本来是一个 y 一个 constrait 一条线有无数个 y, 但是很多线条不需要， 现在就减少了问题空间: working set: 真正有用的线条的集合 >>>> 注意有几个 working-set

这里不同的图片 x,对应不同的一堆框法 y,也就对应一堆线条，也就对应一个 working-set 所以 

一个样本对应一个 working-set.
x1 ---> working-set1:A1
x2 ---> working-set2:A2
x3 ---> working-set3:A3

… 

n 个 x ---> n 个 A
num of samples = num of working-sets

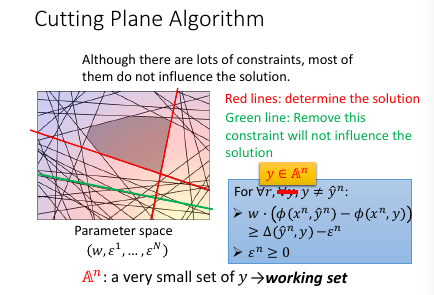
screenshot_2017-06-18_12-05-00.png

cutting plane algo: working set

  1. 初始化 working-set 为空集
  2. 然后解这个最小化问题，获得一个 w.
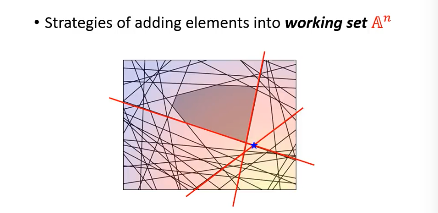
  3. 然后用这个 w 【检查】所有线条，看违反了哪些线条关于【在某一边】的规定，从這些线条中挑出一个违反最严重的加入 working-set
  4. goto step 2

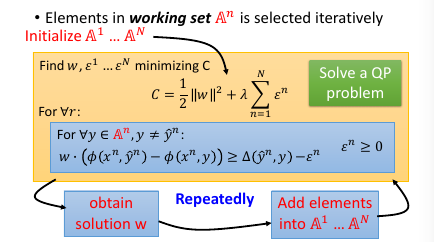
screenshot_2017-06-18_12-08-40.png

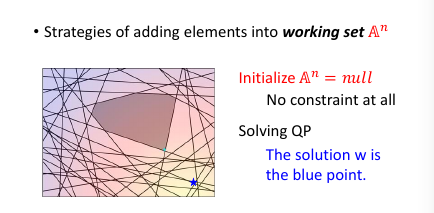
screenshot_2017-06-18_12-09-02.png

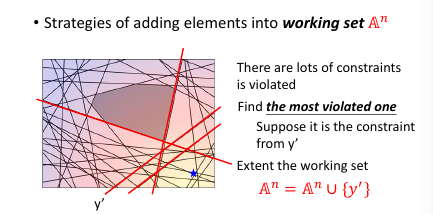
screenshot_2017-06-18_12-12-28.png

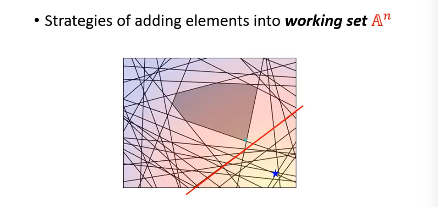screenshot_2017-06-18_12-17-37.png 到这里完成步骤 2. 然后【检查】找到我这个点，违反了哪些线条的规定找到最违反的那一条，把他加入 working-set 作为新的限制条件。然后继续执行步骤 2, 找到下面这个新的解

screenshot_2017-06-18_12-17-55.png

screenshot_2017-06-18_12-20-46.png

screenshot_2017-06-18_12-21-08.png

screenshot_2017-06-18_12-21-38.png

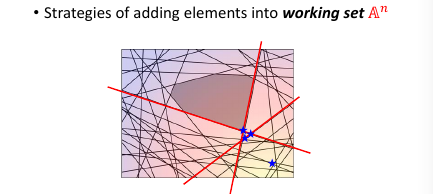
screenshot_2017-06-18_12-16-41.png

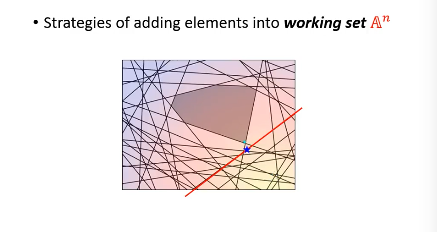
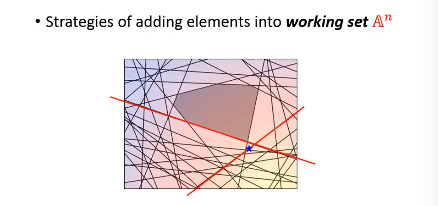
1.8.1 如何衡量【最违反】

screenshot_2017-06-18_12-22-40.png 注意到： ε' 和 w'•φ(x,y^) 这两项都是已知值，最大化时可以不用考虑

1.8.2 Cutting Plane Algo 完整的看

screenshot_2017-06-18_12-28-40.png

screenshot_2017-06-18_12-29-40.png

1.8.3 算法实例 object detection

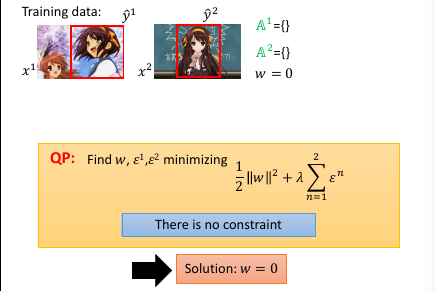
screenshot_2017-06-18_12-32-57.png

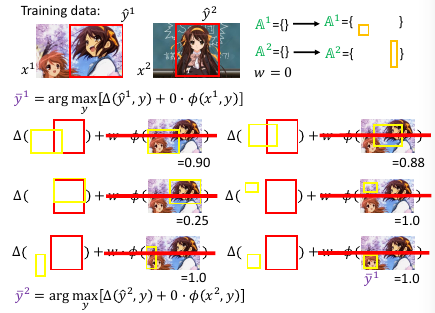
screenshot_2017-06-18_12-38-05.png

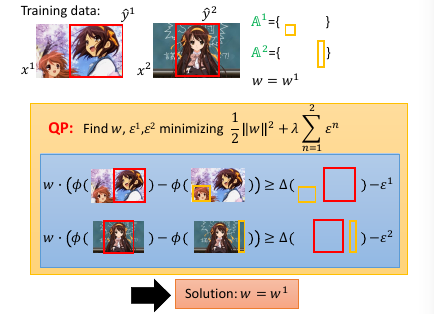
screenshot_2017-06-18_12-40-02.png

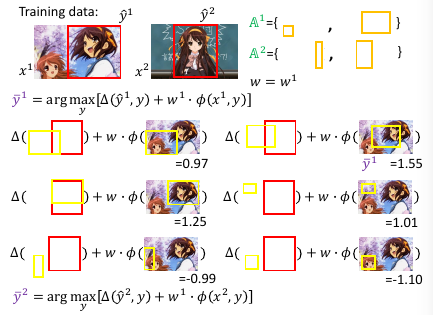
screenshot_2017-06-18_12-41-29.png

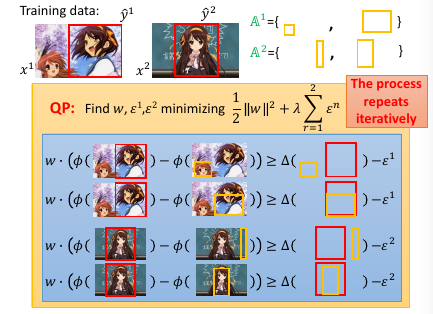
screenshot_2017-06-18_12-44-03.png

还可以进一步的为 最大违反 设置一个 threshold, 也就是对最大违反 进行一个过滤，只要大于某个阈值的 最大违反 才会放到 working-set 中。

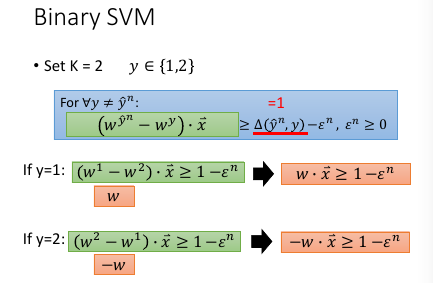
1.9 Multi-class and binary SVM

screenshot_2017-06-18_12-49-50.png

screenshot_2017-06-18_12-50-07.png

screenshot_2017-06-18_12-50-22.png 可以调整哪些 case 比较不容易被 miss recognize

screenshot_2017-06-18_12-50-35.png

1.10 Beyond Structured SVM(open question)

Ref: Hao Tang, Chao-hong Meng, Lin-shan Lee, "An initial attempt for phoneme recognition using Structured Support Vector Machine (SVM)," ICASSP, 2010 Shi-Xiong Zhang, Gales, M.J.F., "Structured SVMs for Automatic Speech Recognition," in Audio, Speech, and Language Processing, IEEE Transactions on, vol.21, no.3, pp.544-555, March 2013

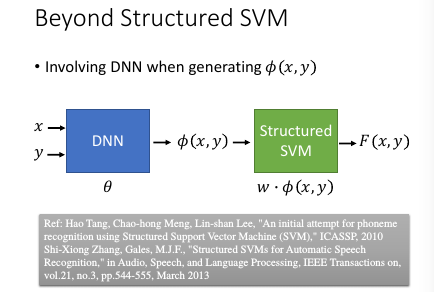screenshot_2017-06-18_12-55-37.png 你要让 structured svm 很厉害，就必须定一套很好的 features 

台大是第一个把 structured svm 用在语音识别的团队
对于某些你不知道该怎么提取 feature 的情况，就应该交给 DNN

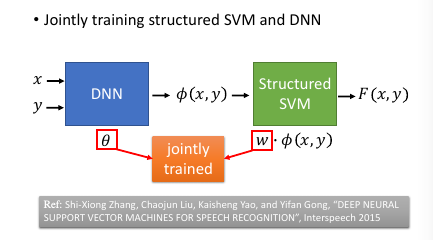screenshot_2017-06-18_12-56-10.png 进展：本来是先 learn 好一个 DNN,然后再接上 SSVM,但是其实可以把两个放在一起 learn. 如果 SSVM 是用 QP 来优化，那确实不好跟 DNN 放在一起，但是如果都用 GD 来优化的话，就可以联合起来 learn.

Ref: Shi-Xiong Zhang, Chaojun Liu, Kaisheng Yao, and Yifan Gong, “DEEP NEURAL SUPPORT VECTOR MACHINES FOR SPEECH RECOGNITION”, Interspeech 2015

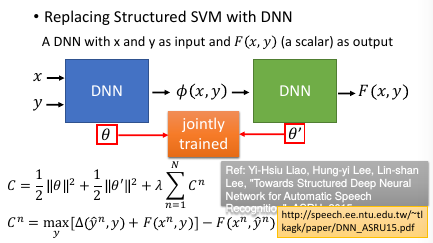screenshot_2017-06-18_12-56-29.png 再进展：都变成 DNN,都用 GD

Date: 2017-06-06

Author: yiddi

Created: 2018-08-12 日 14:55

Validate