lec-24-2 Ensemble Learning
Table of Contents
- 1. Ensemble Learning
- 1.1. Framework of Ensemble
- 1.2. Ensemble: Bagging
- 1.3. Ensemble: Boosting
- 1.3.1. Framework of Boosting
- 1.3.2. How to obtain different classifiers
- 1.3.3. Idea of Adaboost
- 1.3.4. How to re-weighting u1
- 1.3.5. Algo for AdaBoost
- 1.3.6. Toy Example
- 1.3.7. Math background of Adaboost
- 1.3.8. 奇怪的现象
- 1.3.9. Boosting and Bagging
- 1.3.10. General formulation of Boosting
- 1.3.11. Gradient Boosting
- 1.3.12. ft 应该是多少
- 1.3.13. αt 应该是多少
- 1.3.14. Cool Demo
- 1.4. Ensemble: stacking
1 Ensemble Learning
Introduction - We are almost at the end of the semester/final competition. - https://inclass.kaggle.com/c/ml2016-cyber-security-attack-defender/leaderboard - https://www.kaggle.com/c/outbrain-click-prediction/leaderboard - https://www.kaggle.com/c/transfer-learning-on-stack-exchange-tags/leaderboard - You already developed some algorithms and codes. Lazy to modify them. - Ensemble: improving your machine with little modification
1.1 Framework of Ensemble
战法牧,必须每一个都不一样。

1.2 Ensemble: Bagging
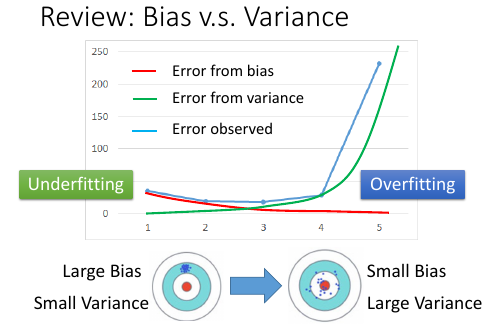
 之间讲过 where error come from:
之间讲过 where error come from:
- bias
- variance
simple model: big bias, small variance complex model : small bias, big variance
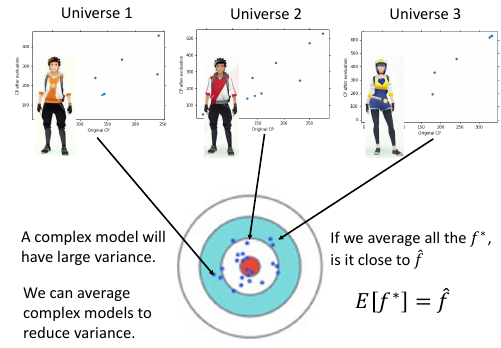
我们可以通过把 [many complex models] 的结果 *平均* 起来,获得 [small variance] 这样可以提高泛化能力(generalization)
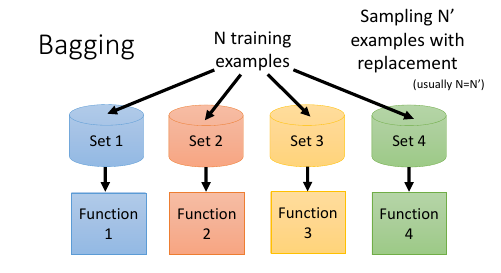
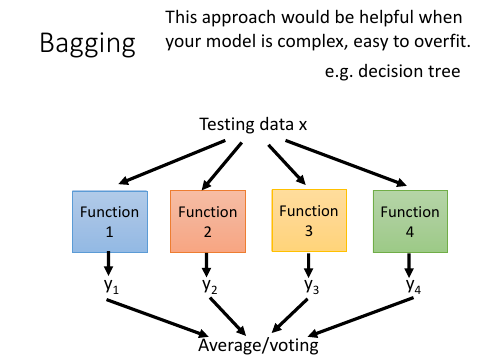
regression -> average classification -> voting 只有当单个模型的能力很强,很容易 overfitting 的时候 Bagging 才是有帮助的。 [注意] NN 是很不容易 overfitting [注意] DT 是 很容易 overfitting
Decision Tree
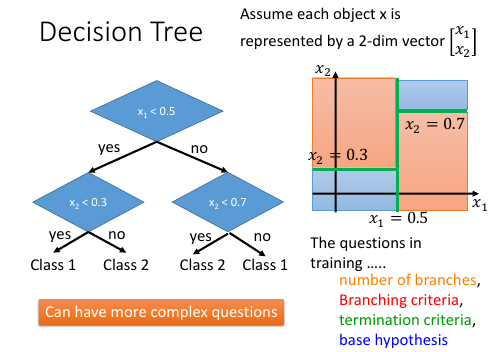 DT 不仅仅是只能切水平 or 垂直的线,可以切很复杂的线
DT 不仅仅是只能切水平 or 垂直的线,可以切很复杂的线
但是 DT 在实际使用的时候有很多参数需要使用启发式方法 Heuristic 来解决: >>> Heuristic ----------------------- 1. num of branches 2. branching criteria 3. termination criteria 4. base hypothesis -----------------------
 用 DT 剪影出初音未来
http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/theano/miku
(1st column: x, 2nd column: y, 3rd column: output (1 or 0) )
用 DT 剪影出初音未来
http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/theano/miku
(1st column: x, 2nd column: y, 3rd column: output (1 or 0) )
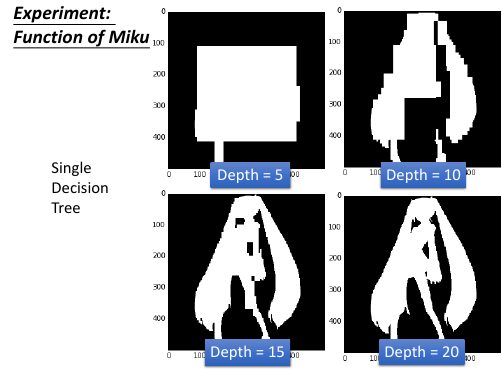 深度为 20 的 DT 就完美了
深度为 20 的 DT 就完美了
DT 是很容易做到 error = 0% 的效果。

为了解决 DT 太容易 overfitting 的问题,用 Bagging >>> RF = Bagging(DTs) ----------------------------------------- 1. Resampling training data 2. Randomly restrict features 3. Randomly restrict questions 以此保证每棵树 data,feature,question 都不一样。 -----------------------------------------
- Decision tree: - Easy to achieve 0% error rate on training data - If each training example has its own leaf - Random forest: Bagging of decision tree - Resampling training data is not sufficient - Randomly restrict the features/questions used in each split - Out-of-bag validation for bagging - Using RF = f2+f4 to test x1 - Using RF = f2+f3 to test x2 .| Out-of-bag (OOB) error: - Using RF = f1+f4 to test x3 .| Good error estimation - Using RF = f1+f3 to test x4 .| of testing set
如果用 out-of-bag 方法验证的话,就不需要再切出额外的 validation set


注意: Bagging 的目标并不是让你在 training data 上的表现得到提升,他只是提升 generalization 的 '让你在 training data 上的表现得到提升' 这件事情是由每一个 DT 决定的。 eg, Depth = 5 的 DT 无法 fit 初音,Bagging 很多 5-depth DT 变成 RF 之后还是无法 fit.
: | Bagging-num of DT ↑ | variance-error ↓ | smoothness ↑ | overfitting ↓ | : | | bias-error = | fittness = | | : |----------------------+-------------------+---------------+----------------| : | RF-num of DT ↑ | variance-error ↓ | smoothness ↑ | overfitting ↓ | : | | bias-error = | fittness = | | : |----------------------+-------------------+---------------+----------------| : | DT-depth ↑ | variance-error ↑ | smoothness = | overfitting ↑ | : | | bias-error = | fittness ↑ | |
Bagging 100 棵 DT 得到的函数的图像,对比 1 棵 DT 的函数的图像是【更平滑】的。
总结 Bagging 只是提升 smoothness, 不提升 fitness
1.3 Ensemble: Boosting
Improving Weak Classifiers Boosting 的目标跟 Bagging 是【相反的】 Bagging 的目标是: 维持 fitness, 提升函数 smoothness, 维持 bias-error, 降低 variance-error, 降低 overfitting Bagging : parallel and independent Boosting : sequentially
1.3.1 Framework of Boosting
 Boosting 的框架是一种【不断补强】的框架,这就要求
Boosting 的框架是一种【不断补强】的框架,这就要求
- f is diversity
- framework is sequencial
1.3.2 How to obtain different classifiers
为了保证获取到不同的分类器,可以用以下措施: 1. 从【数据集】中放回取样形成新的子数据集用来训练不同的分类器 2. 给不同的【数据点】以不同的权重--相当于【模拟其出现次数】,0.4 就是这个点出现 0.4 次 2 就是这个点出现 2 次。这样不同的点不同的权重,就可以获得不同的分类器。 那么新的数据点的表达方式就从 (x1,y1) ---> (x1,y1,u1) 其实改变数据点的权重就相当于改变其出现次数 ---> 相当于改变数据集的 distribution_ 3. 2 中会产生不同的 loss-fn, 因为每个点出现次数不同了,所以 loss-fn 计算所有点出 错之和,也应该根据这个点【出现次数】来相应增加他 error 的比重

1.3.3 Idea of Adaboost

>>> 如何产生【互补】的效果 让 f2 的训练集是 f1 没有看过的并且在 f1 上表现很差的数据 >>> 如何找到让 f1 表现很差的数据 调整 f1 的训练集数据点的 weight: u1 --> u2, 用 u2 去训练 f2. ppt 上 u_1^n : 第 '1' 个分类器的训练集中的第 'n' 个 data >>> 新的衡量分类器在某个数据集表现好坏的标准:ε ε1 = 1 号分类器有错的数据点的 weight 之和 / 1 号分类器所有的数据点的 weight 之和 ε1 总是 < 0.5 的,可以保证这一点,为甚么呢? 如果他大于 0.5 我就把他贰元分类的输出结果 反过来,就保证他又是 < 0.5 的了。 目标是,让 u2 在 1 号分类器上的 ε = 0.5 (刚才分析过 ε 永远 <= 0.5)取其最差情况就是 0.5, 接近 random -- 瞎猜。 >>> 如何调整 u1 成 u2 呢? u2 = 让 u1 中做错的数据权重变大,u1 中做对的数据权重变小 u1 right: u2 <- u1*d1 u1 wrong: u2 <- u1/d1 d1 = sqrt((1-ε1)/ε1)
1.3.4 How to re-weighting u1



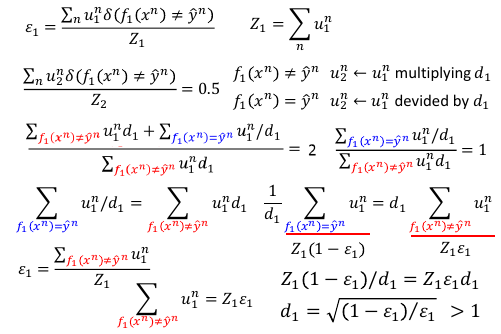
1.3.5 Algo for AdaBoost

T: 找 T 个弱鸡分类器
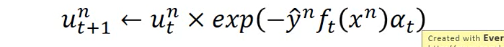

如何整合这个 T 个分类器呢?民主政治:每人投一票(分类器的权重),然后加总计算,看【加总之后结果的正负号】就可以得到贰元结果。精英政治:每个人按照自己的错误率的某个函数 αt 来给不同的票数,余同。
1.3.6 Toy Example
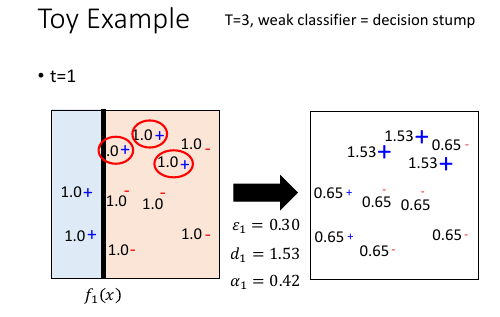 改变 weight 其实就相当于 改变出现次数,也就相当于改变分布(distribution)
改变 weight 其实就相当于 改变出现次数,也就相当于改变分布(distribution)
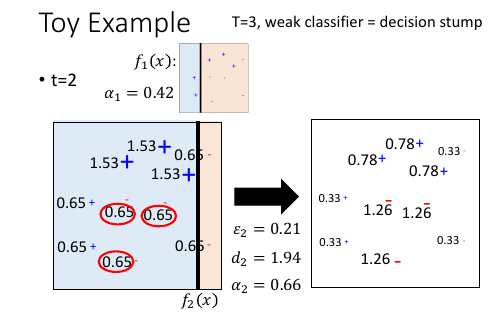 注意每次搞出一个 f ,都要记录下其对应 α,他会是 f 的权重,最后总和所有 f 的时候,要用到。
注意每次搞出一个 f ,都要记录下其对应 α,他会是 f 的权重,最后总和所有 f 的时候,要用到。
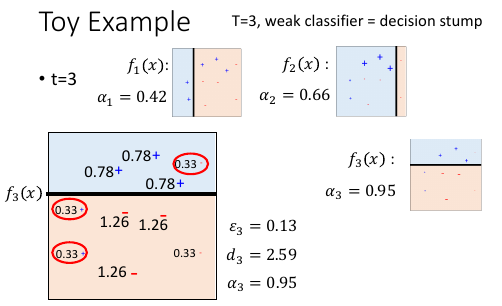
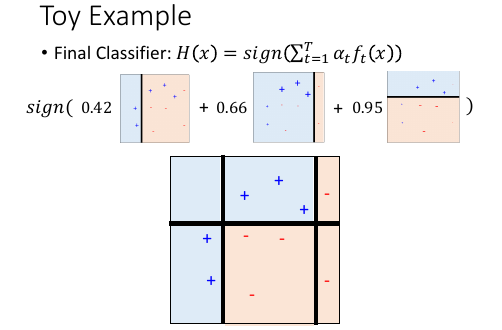 三个 f 把整个平面分成 6 块,每一块的判定结果,都是三个 f 的输出的权重和的符号
三个 f 把整个平面分成 6 块,每一块的判定结果,都是三个 f 的输出的权重和的符号
1.3.7 Math background of Adaboost
 As we have more and more ft (T increases), H(x) achieves smaller
and smaller error rate on training data.
证明:num of ft ^^^ ===> error-rate of H(x) ↓
As we have more and more ft (T increases), H(x) achieves smaller
and smaller error rate on training data.
证明:num of ft ^^^ ===> error-rate of H(x) ↓
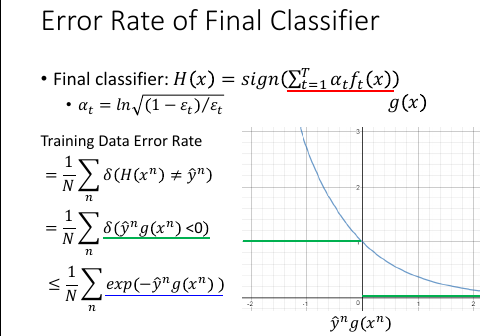 绿色式子有一个 upbound 也就是蓝色划线式子
绿色式子有一个 upbound 也就是蓝色划线式子
 如果能证明 Zt+1 随着 t 越来越大,他越来越小的话,就可以证明这个 error-rate 的 upbound 越来越小。
如果能证明 Zt+1 随着 t 越来越大,他越来越小的话,就可以证明这个 error-rate 的 upbound 越来越小。
 随着 error-rate 的 upbound 越来越小,error-rate 最终就会变成 0
随着 error-rate 的 upbound 越来越小,error-rate 最终就会变成 0
注意: 我们可以 boosting weak classifiers 我们能否 boosting a boosted weak classifier 么? 很显然,不行,boosting 是通过不断更新每个样本点的权重 u 来做的。 而更新权重 ul <- ul-1*d or ul <- ul-1/d d = sqrt((1-ε)/ε) boosting weak classifier 本身就是 error-rate = 0 嵌套 boost, 就会让 d 变成 无穷大, 所以 boosting 的对象只能是 weak classifier
1.3.8 奇怪的现象
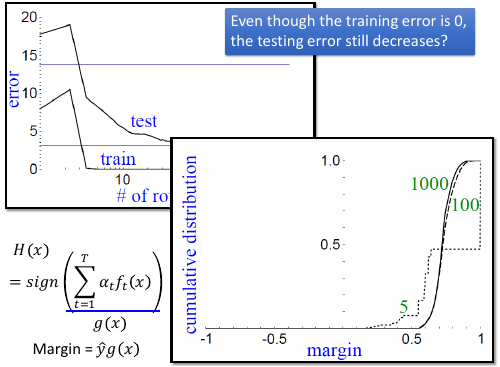 boosting 5 个 classifier 已经让 error-rate 为 0 了。
boosting >5 个 classifier 会让 margin 越来越大。也就是 adaboost 即使在 error-rate 为 0 时,还是会使劲让
margin 更大。
boosting 5 个 classifier 已经让 error-rate 为 0 了。
boosting >5 个 classifier 会让 margin 越来越大。也就是 adaboost 即使在 error-rate 为 0 时,还是会使劲让
margin 更大。
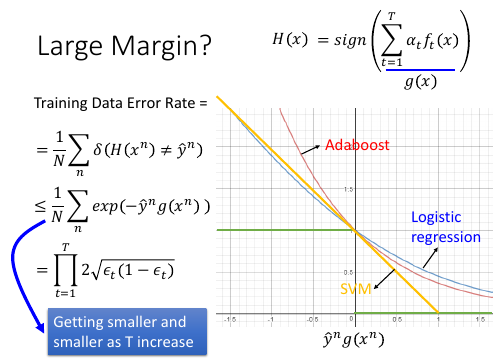 Adaboost 虽然没有明确的最小化某个函数,但是他确实让 upbound 这个表达式越来越小。
Adaboost 虽然没有明确的最小化某个函数,但是他确实让 upbound 这个表达式越来越小。
1.3.9 Boosting and Bagging
Bagging -> random forest Boosting -> Adaboost


s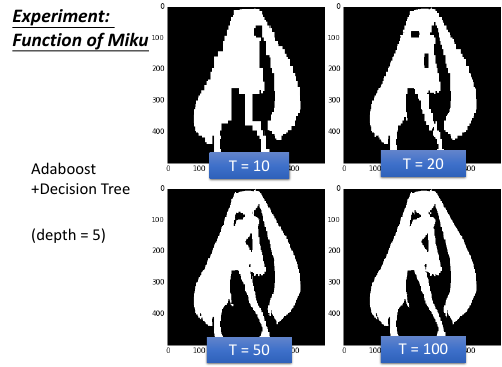 可以看到:
可以看到:
>>> Bagging and Boosting --------------------------------------------------------------------------- Bagging 只是降低 overfitting 增加函数 smoothness, Bagging 之后的模型的能力没有增强 Boosting 没有增加函数 smoothness, 但是 Boosting 之后模型的能力却加强了 这也符合 Boosting 的特点--所有的 classifer 都是互补的 ---------------------------------------------------------------------------
>>> Bagging . | Bagging-num of DT ↑ | variance-error ↓ | smoothness ↑ | overfitting ↓ | . | | bias-error = | fittness = | power of model = | . |----------------------+-------------------+---------------+-------------------| . | RF-num of DT ↑ | variance-error ↓ | smoothness ↑ | overfitting ↓ | . | | bias-error = | fittness = | power of model = | . |----------------------+-------------------+---------------+-------------------| . | DT-depth ↑ | variance-error ↑ | smoothness = | overfitting ↑ | . | | bias-error = | fittness ↑ | power of model ↑ |
>>> Boosting . | Boosting-num of f ↑ | variance-error = | smoothness ↑ | overfitting ↑ | . | | bias-error ↓ | fittness ↑ | power of model ↑ | . |----------------------+------------------+---------------+-------------------| . | Adaboost-num of f ↑ | variance-error = | smoothness ↑ | overfitting ↑ | . | | bias-error ↓ | fittness ↑ | power of model ↑ | . |----------------------+------------------+---------------+-------------------| . | power of f = | variance-error = | smoothness = | overfitting = | . | | bias-error = | fittness = | power of model = |
1.3.10 General formulation of Boosting
 看似单个 classifier 没有 loss-fn, 但是整体看统合后的模型 g(x) 是有 loss-fn 的。定这个 loss-fn 可以自主定义。比如这里使用 Σexp(-y*g(x))
看似单个 classifier 没有 loss-fn, 但是整体看统合后的模型 g(x) 是有 loss-fn 的。定这个 loss-fn 可以自主定义。比如这里使用 Σexp(-y*g(x))
1.3.11 Gradient Boosting
 因为之前通过推导已经得到过 gt 与 gt-1 的关系,是一种类似递归的关系,而回忆 GD 是如何优化 w 的,发现 GD 方法最后给出的表达式,也是这样的关系。所以,只要这两项(红方框)是方向相同的即可。
因为之前通过推导已经得到过 gt 与 gt-1 的关系,是一种类似递归的关系,而回忆 GD 是如何优化 w 的,发现 GD 方法最后给出的表达式,也是这样的关系。所以,只要这两项(红方框)是方向相同的即可。
1.3.12 ft 应该是多少
那怎么找一个 ft 与 上面那个红方框具有 same direction 呢? 把所有的 ft 与 所有的 exp 都各自组成向量,同方向就代表我希望 他们两个向量的内积越大越好,内积展开出来就是 Σexp(...)(y)ft maximize 这个和式就代表 尽量让上图两个红方框 具有相同的方向

每次做 adaboost 的时候,每次都会给 sample 乘以这样的一个 weight.
循环到 t 次时,每一个 smaple 累积下来都扩大了 ∏exp(xxx) 倍了。
我们现在要找一个 ft,他能够 minize training data 上的 error.
每一个 data 都用这样的 weight(t 次累乘).
所以你会发现,如果用 Gradient Boosting 的想法,你定义的 loss-fn 就是
刚才的 exp(xxx) 的话。你找出来的 ft,他其实就是 adaboost 里面找出来的 ft.
今天用 Gradient boosting,他是一个更 general 的想法。因为,你可以更改
各种不同的 loss-fn.
从另一个角度可以看出,Adaboost 其实就是在 minized 那个 exp(xxx) 的 loss-fn
1.3.13 αt 应该是多少

利用 Gradient descent 来优化 loss-fn,
为了确定 αt,最理想的方法是【穷举】所有可能的取值,看哪个会让 loss-fn
最小。 但是既然已经有了 ft,不如直接复用 ft:
我就看,固定 ft 的前提下,αt 取什么值可以让 loss-fn 最小。
解 αt 看哪个 αt 可以让 loss-fn 的微分是 0 即可。
1.4 Ensemble: stacking
Average Vote : 每人持一票 Majority Vote : 每人持票数不等 不是人来决定谁持票多少, 而是机器学习之后决定每个人的持票数目
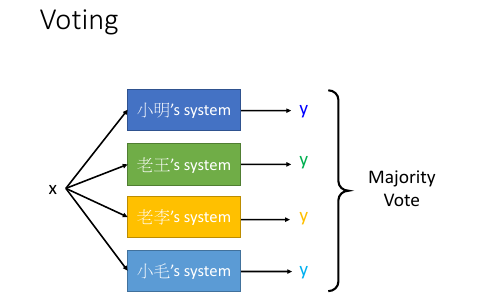
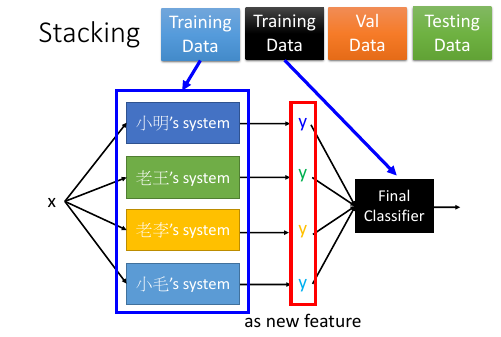
把四个人的模型的输出,共同组成一个 4 维度向量--一个新的样本点,然后输入给一个 classifier 然后根据标签值和误差,学习出每个人的 weight
但是这种模型,一定要注意: 把 Training Data 分成两份,一个拿来 train 前面的四种模型,一个拿来 train 最后的 'Final Classifier'.