lec-27 Spatial Transformer Layer
Table of Contents
1 Spatial Transformer Layer
Special Structure 之一, 让 CNN 具备【移动,放缩,旋转】图形的识别能力 Give CNN the ability to detect the [movement, scaling, rotation] version of original Image. 普通的 CNN 是完全不具备这种能力的。
1.1 普通 CNN 的弊端
movement scaling ratation 无力
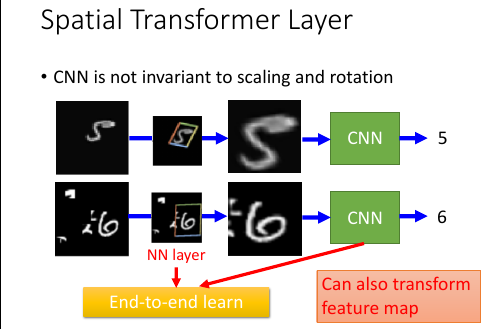
普通的 CNN 最大的部件就是 filter 和 pooling, 这两个决定了 CNN 不具备:
movement: 依赖 max-pooling 能稍微检测移动一丢丢的东西,但是稍远就不行scaling: filter 是固定大小的,他能 match 的模式肯定也是固定大小的rotation: filter 的各个数值都是固定的,他能 match 的模式是固定的。换言之,图像中的内容 [放大或缩小][旋转][移动] 之后就无法被识别了。
- 需要增加一个 spatial transformer layer STL 的能力是提供: [移动,旋转,缩放]图片到 CNN 可以识别的程度。 STL 需要训练,以调整参数可以【恰当】的实现上述三个功能。
- spatial can jointly train with CNN STL 相当于图片的 pre-training 阶段,但是可以与 CNN 一起训练,而且也应该一起训练,以期两者可以相互配合,也使两者的参数是相互配合的。
- spatial can also transform feature map 因为 feature map 也可以作为一个特殊的 'image' 来看待,所以当然可以用来对其进行这种预处理:spatial transform
1.2 放缩、移动、旋转的数学原理
1.2.1 线性代数 movement 原理
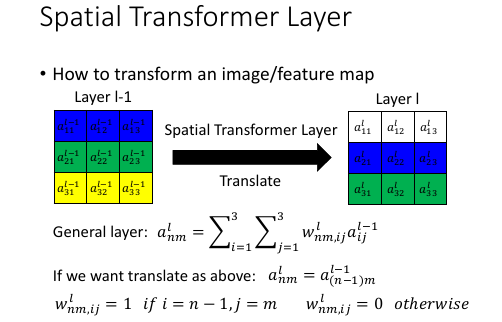 [勘误] 不应该是 anm = a(n-1)m; 应该是 a(n+1)m
虽然 hiden layer 的输出是一个长的 vector, 但是如果编号得当是完全可以实现精细化控制的---排布成矩阵,矩阵长于此。只需要转换矩阵 W 给的得当即可实现对原来矩阵的旋转和缩放。
[勘误] 不应该是 anm = a(n-1)m; 应该是 a(n+1)m
虽然 hiden layer 的输出是一个长的 vector, 但是如果编号得当是完全可以实现精细化控制的---排布成矩阵,矩阵长于此。只需要转换矩阵 W 给的得当即可实现对原来矩阵的旋转和缩放。
. l-1 l . --------------------------- . ap -> Σ_p(wp,q) -> aq . | | . v v . aij -> wij,nm -> anm . 千万注意这里 w 中 q p 的顺序,切记。 movement, 上下平移: l:anm = l-1:a(n+1)m 一旦找到这种平移的行列关系,就可以通过将对应 W 某些位置置 1,其余置 0 的方式 实现平移 l:wnm,ij = 1, if i = n+1, j = m; l:wnm,ij = 0, otherwise layer l-1: a b c d e f g h i . nm 00 01 02 10 11 12 20 21 22 . -------- -------- -------- . ----- ----- ----- . q 0 1 2 3 4 5 6 7 8 . T ij p +-+-+-+-+-+-+-+-+-+ . a 00 | 0 |0|0|0|1|0|0|0|0|0| 0 . | +-+-+-+-+-+-+-+-+-+ . b 01 | 1 |0|0|0|0|1|0|0|0|0| 0 . | +-+-+-+-+-+-+-+-+-+ . c 02 | 2 |0|0|0|0|0|1|0|0|0| 0 . +-+-+-+-+-+-+-+-+-+ . d 10 | 3 |0|0|0|0|0|0|1|0|0| a . • | +-+-+-+-+-+-+-+-+-+ = . e 11 | 4 |0|0|0|0|0|0|0|1|0| b . | +-+-+-+-+-+-+-+-+-+ . f 12 | 5 |0|0|0|0|0|0|0|0|1| c . +-+-+-+-+-+-+-+-+-+ . g 20 | 6 |0|0|0|0|0|0|0|0|0| d . | +-+-+-+-+-+-+-+-+-+ . h 21 | 7 |0|0|0|0|0|0|0|0|0| e . | +-+-+-+-+-+-+-+-+-+ . i 22 | 8 |0|0|0|0|0|0|0|0|0| f . +-+-+-+-+-+-+-+-+-+ . +-+-+-+ +-+-+-+ . |a|b|c| |0|0|0| . +-+-+-+ +-+-+-+ . |d|e|f| ---> W ---> |a|b|c| . +-+-+-+ +-+-+-+ . |g|h|i| |d|e|f| . +-+-+-+ +-+-+-+
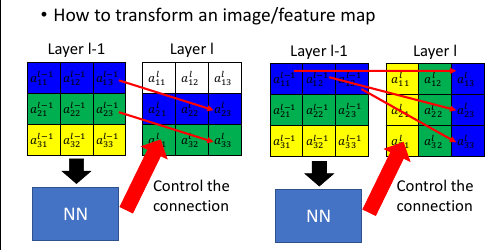 不仅平移,旋转,放缩也是如此,步骤:
不仅平移,旋转,放缩也是如此,步骤:
- 画出矩阵图
- 写下对应位置下标,找出内在关系
- 尝试给出 W
1.2.2 线性代数 scaling 原理
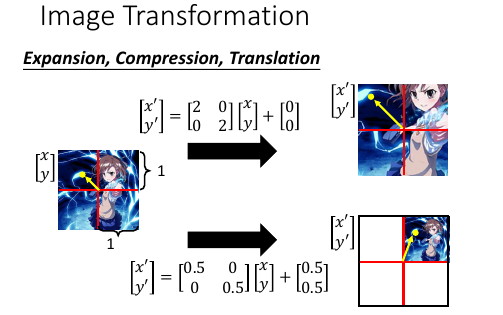
缩放平移步骤: 1) 根据图片横纵轴,得到图片中心,以该中心为原点建立坐标系,每个像素点都是一个向量 下面就可以使用向量和矩阵运算来表示像素级别关系 2) *转换后坐标 = 旋转矩阵 × 原坐标 + 移动向量* 3) 原地放缩使用对角矩阵 比如原来的像素点是 (x,y), 放大后是 (2x,3y) 所以对角矩阵就是: . +--+--+ . |2 |0 | . +--+--+ . |0 |3 | . +--+--+ 4) 原地放缩后移动,就使用对角矩阵加向量加减法 比如原来像素点是 (x,y), 缩小并移动后是(0.5x+0.5, 0.5y+0.8) . +--+ +---+---+ +-+ +---+ . |x'| |0.5|0 | |x| |0.5| . +--+ = +---+---+ *+-+ + +---+ . |y'| |0 |0.5| |y| |0.8| . +--+ +---+---+ +-+ +---+
1.2.3 线性代数 rotation 原理
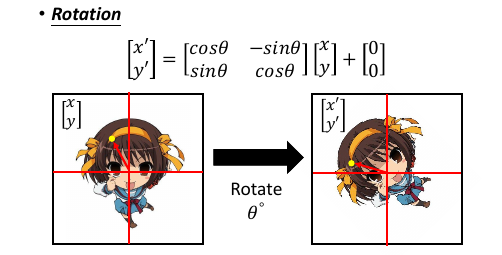 从原图 (x,y) 逆时针 旋转θ,使用这个矩阵
从原图 (x,y) 逆时针 旋转θ,使用这个矩阵
1.3 Spatial Transfomer Layer 简介
- 另一种发问方式上面的数学基础部分都是这种模式:告诉你一张图片,告诉你如何 [放缩,平移,旋转] ,然后问你会生成的图片是什么样子。这样生成的图片是对原始图片进行【全转换】,64*64 正方图 -> 128*128 菱形图 (旋转放大) 这并不是我们需要的样式,我们需要的是 . a. 固定目标图的大小和形状, . b. 仅仅对原始图像的一部分做转换 因此需要另一种【倒叙的】发问方式: 原图中哪些位置的像素对目标图中的像素有贡献。
- ST 要做什么? ST 是要生成一张图片,而这个图片可以被 CNN 正确识别,所以 ST 的作用是对 image 进行 pre-training. 原图经过 ST 转换成一张适当【放缩,移动,旋转】过的图片。
- ST 要完成 2 件事情:
- 找到目标图中每一个像素跟原图中的对应位置 …….. localisation
- 通过 1) 找到的对应位置,对原图进行转换生成目标图.. interpolation
1.3.1 Localisation fn
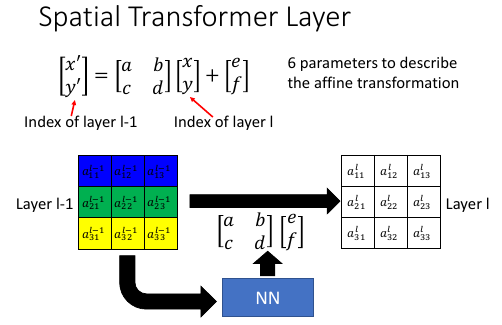
这个 Localisation-fn 就是一个 NN ,这个 NN 接受一整张 image 作为 input, 输出的是一个 6 维度的向量
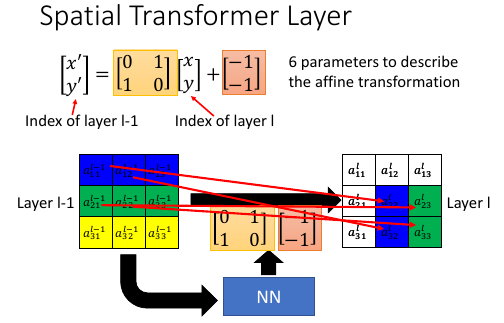
- [放缩、移动、旋转] 這些变化的总称是 affine transformation
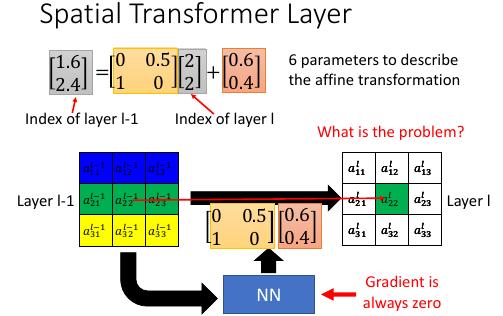
- 又见 Gradient 对于离散问题的无力如何理解 Gradient, 就是 权重参数小小的变化是否可以在结果上有所反映。 本问题,‘结果’ 就是 原图坐标,'权重参数' 就是 ppt 中的矩阵这里: 原图位置 = 权重参数矩阵 * 目标图位置 + 位置偏移由于‘原图位置’ 和 '目标位置' 都是‘位置’---一个离散量。权重参数的微小变化,根本不会改变‘原图位置’。仅以此即可判断 Gradient 无法处理这里的问题,因为优化步骤会被打断。 Gradient is always zero
1.3.2 Grid generator: interpolation
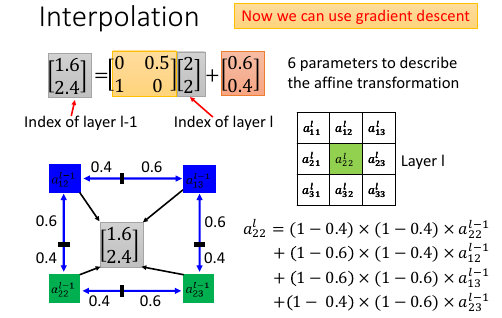 从 localisatin 得到的 index 也许并不是整数,这时候需要做 interpolation:
撷取其周围四个点的坐标的像素值,按照距离远近做 weighted sum.
从 localisatin 得到的 index 也许并不是整数,这时候需要做 interpolation:
撷取其周围四个点的坐标的像素值,按照距离远近做 weighted sum.
. localisation of [2,2] = [1.6, 2.4] . . 1 < 1.6 < 2; . 2 < 2.4 < 3; . . al-1: [1.6,2.4] . +-----------+-----------+----------+ . | | | | . v v v v . al-1: [1,2] [1,3] [2,2] [2,3] . | | | | . | | | | . |1.6-1|* |1.6-1|* |1.6-2|* |1.6-2|* . |2.4-2|= |2.4-3|= |1.6-2|= |2.4-3|= . ---------v-----------v-----------v----------v----------- . 0.24* 0.36* 0.16* 0.24* . al-1: a12 a13 a22 a23 + . -------------------------------------------------------- . \ | | / . \ | | / . --------------------------------- . v . al: a22
1.3.3 ST = local + grid
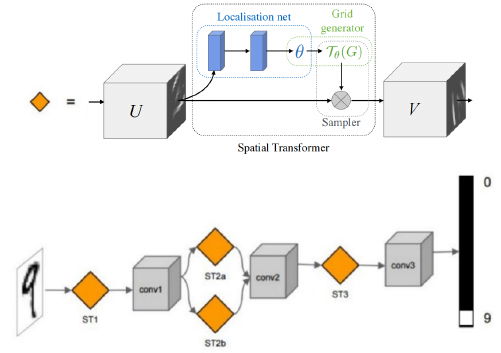
- Spatial Transformer = localisation net + Grid generator Localisation Net 就是上页 ppt 中产生 6 个参数的 NN. Grid generator 就是上页 ppt 中生成图像的过程,用 interpolation 方法产生目标图像。
- 可以在同一层放两个 spatial transformer, 如 ST2a,ST2b
1.4 Spatial Transfomer 具体应用
1.4.1 MNIST 识别
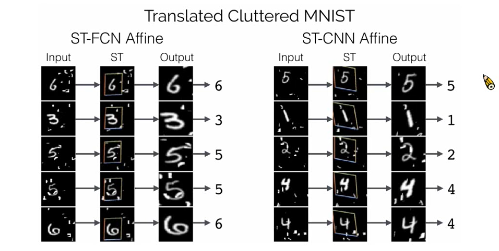
1.4.2 街牌号识别
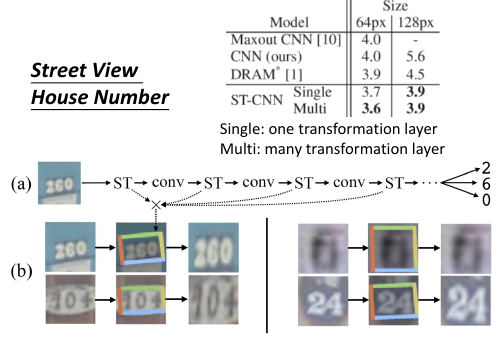
输出的是 55 维度的向量,因为门牌号最多有 5 个数字,每个数字对应 11 维度,前 10 维度对应 0~9, 最后一维代表有没有数字(null)。因为有可能是 3 个数字。
每一个 conv 操作之后就做一次 ST(spatial transfomation)
图中给出了多次 ST 总和起来的作用,可能是【放缩,旋转,移动】都有
1.4.3 鸟类识别
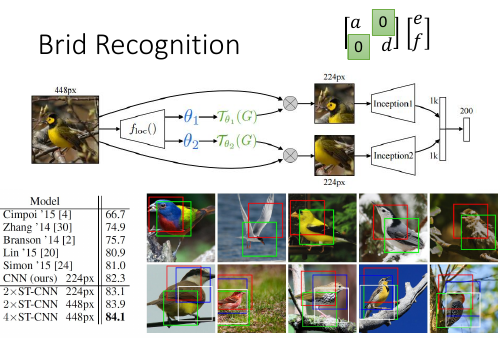 这里的 localisation 函数是只有 4 个参数,固定了矩阵的‘绿色方块’。也就是说这个 localisatin fn 只能做 [放缩,移动,
这里的 localisation 函数是只有 4 个参数,固定了矩阵的‘绿色方块’。也就是说这个 localisatin fn 只能做 [放缩,移动, 旋转 ]