scikit-笔记12:交叉验证

In the previous sections and notebooks, we split our dataset into two parts, a training set and a test set. We used the training set to fit our model, and we used the test set to evaluate its generalization performance – how well it performs on new, unseen data. ​ ​

However, often (labeled) data is precious, and this approach lets us only use ~ 3/4 of our data for training. On the other hand, we will only ever try to apply our model 1/4 of our data for testing. A common way to use more of the data to build a model, but also get a more robust estimate of the generalization performance, is cross-validation.

In cross-validation, the data is split repeatedly into a training and non-overlapping test-sets, with a separate model built for every pair. The test-set scores are then aggregated for a more robust estimate.

The most common way to do cross-validation is k-fold cross-validation, in which the data is first split into k (often 5 or 10) equal-sized folds, and then for each iteration, one of the k folds is used as test data, and the rest as training data:

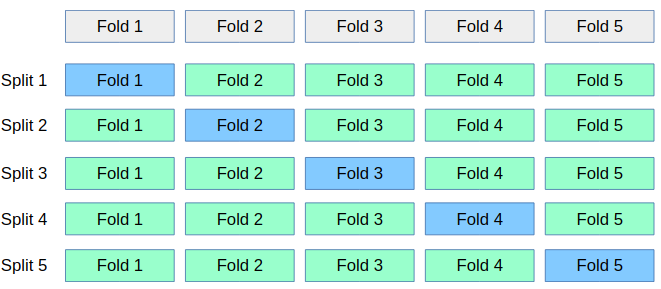
This way, each data point will be in the test-set exactly once, and we can use all but a k'th of the data for training. Let us apply this technique to evaluate the KNeighborsClassifier algorithm on the Iris dataset:

from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
iris = load_iris()
X, y = iris.data, iris.target
print(X.shape, y.shape)
classifier = KNeighborsClassifier()

The labels in iris are sorted, which means that if we split the data as illustrated above, the first fold will only have the label 0 in it, while the last one will only have the label 2:

y

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

To avoid this problem in evaluation, we first shuffle our data:

import numpy as np
rng = np.random.RandomState(0)
permutation = rng.permutation(len(X))
X, y = X[permutation], y[permutation]
print(y)

Now implementing cross-validation is easy:

k = 5
n_samples = len(X)
fold_size = n_samples // k
scores = []
masks = []
for fold in range(k):
    # generate a boolean mask for the test set in this fold
    test_mask = np.zeros(n_samples, dtype=bool)
    test_mask[fold * fold_size : (fold + 1) * fold_size] = True
    # store the mask for visualization
    masks.append(test_mask)
    # create training and test sets using this mask
    X_test, y_test = X[test_mask], y[test_mask]
    X_train, y_train = X[~test_mask], y[~test_mask]
    # fit the classifier
    classifier.fit(X_train, y_train)
    # compute the score and record it
    scores.append(classifier.score(X_test, y_test))

Let's check that our test mask does the right thing:

import matplotlib.pyplot as plt
plt.matshow(masks, cmap='gray_r')

<matplotlib.image.AxesImage at 0x7f9c3281ac50>

And now let's look a the scores we computed:

print(scores)
print(np.mean(scores))

As you can see, there is a rather wide spectrum of scores from 90% correct to 100% correct. If we only did a single split, we might have gotten either answer.

As cross-validation is such a common pattern in machine learning, there are functions to do the above for you with much more flexibility and less code. The sklearn.model_selection module has all functions related to cross validation. There easiest function is cross_val_score which takes an estimator and a dataset, and will do all of the splitting for you:

from sklearn.model_selection import cross_val_score
scores = cross_val_score(classifier, X, y)
print(scores)
print(np.mean(scores))

As you can see, the function uses three folds by default. You can change the number of folds using the cv argument:

cross_val_score(classifier, X, y, cv=5)

array([ 1.  ,  0.93,  1.  ,  1.  ,  0.93])

There are also helper objects in the cross-validation module that will generate indices for you for all kinds of different cross-validation methods, including k-fold:

from sklearn.model_selection import KFold, StratifiedKFold, ShuffleSplit