UP | HOME

scikit-笔记19:非监督学习-基于结构化和密度估计的clustering方法

Table of Contents

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt

1 Unsupervised learning: Hierarchical and density-based clustering algorithms

1.1 two clustering methods better than K-Means

In a previous notebook, "08 Unsupervised Learning - Clustering.ipynb", we introduced one of the essential and widely used clustering algorithms, K-means. One of the advantages of K-means is that it is extremely easy to implement, and it is also computationally very efficient compared to other clustering algorithms.

However, we've seen that one of the weaknesses of K-Means is that it only works well if the data can be grouped into a globular or spherical shape. Also, we have to assign the number of clusters, k, a priori – this can be a problem if we have no prior knowledge about how many clusters we expect to find.

Summarizing: short-commings of K-means:

So we have 4 short-comings of K-means:

  1. Incorrect number of clusters <<< solved by elbow-method
  2. Anisotropicly distributed data
  3. Different variance
  4. Unevenly sized blobs

In this notebook, we will take a look at 2 alternative approaches to clustering,

  • hierarchical clustering
  • density-based clustering.

2 Hierarchical Clustering

One nice feature of hierachical clustering is that we can visualize the results as a dendrogram, a hierachical tree. Using the visualization, we can then decide how "deep" we want to cluster the dataset by setting a "depth" threshold. Or in other words,

overcome K-means by: >>> we don't need to make a decision about the number of clusters upfront.

2.1 Agglomerative and divisive hierarchical clustering

Furthermore, we can distinguish between 2 main approaches to hierarchical clustering:

  • Divisive clustering
  • Agglomerative clustering.

In agglomerative clustering, we start with a single sample from our dataset and iteratively merge it with other samples to form clusters – we can see it as a bottom-up approach for building the clustering dendrogram.

In divisive clustering, however, we start with the whole dataset as one cluster, and we iteratively split it into smaller subclusters – a top-down approach.

In this notebook, we will use agglomerative clustering.

2.2 agglomerative hierachical cluetering

2.2.1 how to measure similarity between two samples

Now, the next question is how we measure the similarity between samples. One approach is the familiar Euclidean distance metric that we already used via the K-Means algorithm. As a refresher, the distance between 2 m-dimensional vectors \(\mathbf{p}\) and \(\mathbf{q}\) can be computed as:

\begin{align} \mathrm{d}(\mathbf{q},\mathbf{p}) & = \sqrt{(q_1-p_1)^2 + (q_2-p_2)^2 + \cdots + (q_m-p_m)^2} \\[8pt] & = \sqrt{\sum_{j=1}^m (q_j-p_j)^2}.\end{align}

However, that's the distance between 2 samples. Now, how do we compute the similarity between subclusters of samples in order to decide which clusters to merge when constructing the dendrogram? I.e., our goal is to iteratively merge the most similar pairs of clusters until only one big cluster remains. There are many different approaches to this, for example single and complete linkage.

2.2.2 how to measure similarity between two clusters

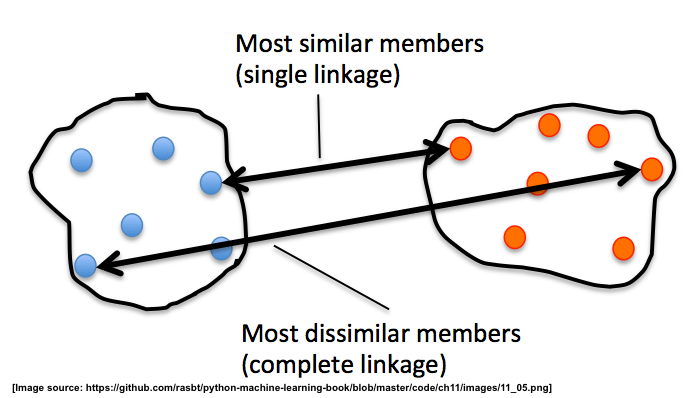
Single and complete linkage

In single linkage, we take the pair of the most similar samples in each cluster (based on the Euclidean distance, for example), means one of two from one cluster, the other one from another cluster — one sample from one cluster.And merge the two clusters which have the most similar 2 members into one new, bigger cluster.

In complete linkage, we compare the pairs of the two most dissimilar members of each cluster with each other, and we merge the 2 clusters where the distance between its 2 most dissimilar members is smallest.

clustering-linkage.png

2.2.3 applying agglomerative clustering by labeled datasets

Why using labeled datset, convenient to check the result.

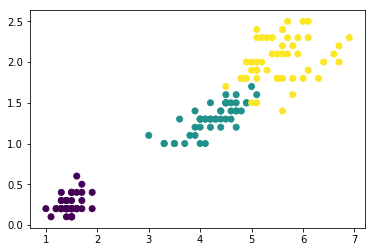
To see the agglomerative, hierarchical clustering approach in action, let us load the familiar Iris dataset – pretending we don't know the true class labels and want to find out how many different follow species it consists of: 

from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, [2, 3]] #<- using only the 3rd and 4th features
                         #   easy to visualize
y = iris.target
n_samples, n_features = X.shape
plt.scatter(X[:, 0], X[:, 1], c=y);

3199qbE.png

2.2.3.1 draw dendrogram by scipy.cluster.hierarchy.dendrogram after compute the similarity by scipy.cluster.hierachy.linkage

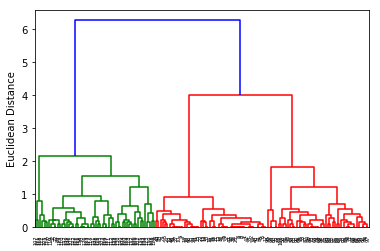
First, we start with some exploratory clustering, visualizing the clustering dendrogram using SciPy's linkage and dendrogram functions: 

from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
clusters = linkage(X,
                   metric='euclidean', #<- method to evalute the similarity
                   method='complete'   #<- method to combine two cluster
)
dendr = dendrogram(clusters)
plt.ylabel('Euclidean Distance');

3199Grq.png

2.2.3.2 build agglomerative model by sklearn.cluster.AgglomerativeClustering

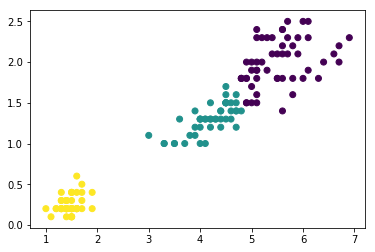
Next, let's use the AgglomerativeClustering estimator from scikit-learn and divide the dataset into 3 clusters. Can you guess which 3 clusters from the dendrogram it will reproduce? 

from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3,
                             affinity='euclidean', #<- method to compute similarity
                             linkage='complete')   #<- method to combine two cluster
prediction = ac.fit_predict(X)
print('Cluster labels: %s\n' % prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction);

3199T1w.png

3 Density-based Clustering - DBSCAN

3.0.1 what is DBSCAN

Another useful approach to clustering is Density-based Spatial Clustering of Applications with Noise (DBSCAN).

In essence, we can think of DBSCAN as an algorithm that divides the dataset into subgroup based on dense regions of point.

3.0.2 3 kinds of points

In DBSCAN, we distinguish between 3 different "points",

  • Core points: A core point is a point that has at least a minimum number of other points (MinPts) in its radius epsilon.
  • Border points: A border point is a point that is not a core point, since it doesn't have enough MinPts in its neighborhood, but lies within the radius epsilon of a core point.
  • Noise points: All other points that are neither core points nor border points.

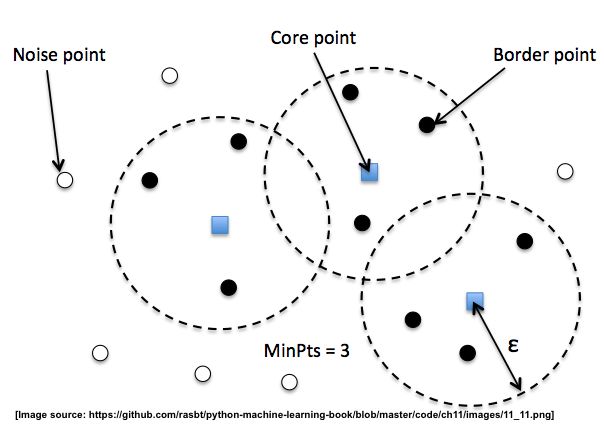
dbscan.png

we can split them by two evidence:

  • MinPts
  • with in the radius of core point

A nice feature about DBSCAN is that we don't have to specify a number of clusters upfront. However, it requires the setting of additional hyperparameters such as the:

  • value for MinPts
  • radius epsilon.
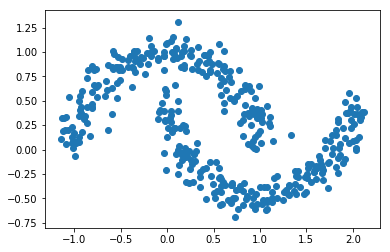
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=400,
                  noise=0.1,
                  random_state=1)
plt.scatter(X[:,0], X[:,1])
plt.show()

3199g_2.png 

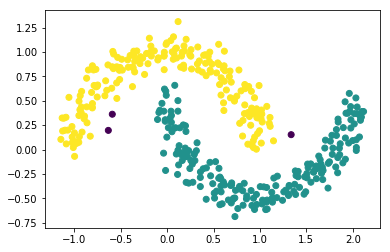
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2,               #<- radius epsilon
            min_samples=10,        #<- MinPts
            metric='euclidean')
prediction = db.fit_predict(X)
print("Predicted labels:\n", prediction)
plt.scatter(X[:, 0], X[:, 1], c=prediction);

3199SJG.png

4 Exercise

EXERCISE: Using the following toy dataset, two concentric circles, experiment with the three different clustering algorithms that we used so far: KMeans, AgglomerativeClustering, and DBSCAN. Which clustering algorithms reproduces or discovers the hidden structure (pretending we don't know y) best? Can you explain why this particular algorithm is a good choice while the other 2 "fail"? 

from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1500,
                    factor=.4,
                    noise=.05)
plt.scatter(X[:, 0], X[:, 1], c=y);

8573TSC.png

5 Misc tools

5.1 scikit-learn

5.1.1 ML models by now

  1. from sklearn.datasets import make_blobs
  2. from sklearn.datasets import make_moons *
  3. from sklearn.datasets import make_circles *
  4. from sklearn.datasets import make_regression
  5. from sklearn.datasets import load_iris
  6. from sklearn.datasets import load_digits
  7. from sklearn.datasets import load_breast_cancer
  8. from sklearn.model_selection import train_test_split
  9. from sklearn.model_selection import cross_val_score
  10. from sklearn.model_selection import KFold
  11. from sklearn.model_selection import StratifiedKFold
  12. from sklearn.model_selection import ShuffleSplit
  13. from sklearn.model_selection import GridSearchCV
  14. from sklearn.model_selection import learning_curve
  15. from sklearn.feature_extraction import DictVectorizer
  16. from sklearn.feature_extraction.text import CountVectorizer
  17. from sklearn.feature_extraction.text import TfidfVectorizer
  18. from sklearn.feature_selection import SelectPercentile
  19. from sklearn.feature_selection import f_classif
  20. from sklearn.feature_selection import f_regression
  21. from sklearn.feature_selection import chi2
  22. from sklearn.feature_selection import SelectFromModel
  23. from sklearn.feature_selection import RFE
  24. from sklearn.linear_model import LogisticRegression
  25. from sklearn.linear_model import LinearRegression
  26. from sklearn.linear_model import Ridge
  27. from sklearn.linear_model import Lasso
  28. from sklearn.linear_model import ElasticNet
  29. from sklearn.neighbors import KNeighborsClassifier
  30. from sklearn.neighbors import KNeighborsRegressor
  31. from sklearn.preprocessing import StandardScaler
  32. from sklearn.decomposition import PCA
  33. from sklearn.metrics import confusion_matrix, accuracy_score
  34. from sklearn.metrics import adjusted_rand_score
  35. from sklearn.metrics.scorer import SCORERS
  36. from sklearn.metrics import r2_score
  37. from sklearn.cluster import KMeans
  38. from sklearn.cluster import KMeans
  39. from sklearn.cluster import MeanShift
  40. from sklearn.cluster import DBSCAN # <<< this algorithm has related sources in LIHONGYI's lecture-12
  41. from sklearn.cluster import AffinityPropagation
  42. from sklearn.cluster import SpectralClustering
  43. from sklearn.cluster import Ward
  44. from sklearn.cluster import DBSCAN *
  45. from sklearn.cluster import AgglomerativeClustering *
  46. from scipy.cluster.hierarchy import linkage *
  47. from scipy.cluster.hierarchy import dendrogram *
  48. from sklearn.metrics import confusion_matrix
  49. from sklearn.metrics import accuracy_score
  50. from sklearn.metrics import adjusted_rand_score
  51. from sklearn.metrics import classification_report
  52. from sklearn.preprocessing import Imputer
  53. from sklearn.dummy import DummyClassifier
  54. from sklearn.pipeline import make_pipeline
  55. from sklearn.svm import LinearSVC
  56. from sklearn.svm import SVC
  57. from sklearn.tree import DecisionTreeRegressor
  58. from sklearn.ensemble import RandomForestClassifier
  59. from sklearn.ensemble import GradientBoostingRegressor