lec-03 Gradient descent
Table of Contents
1 Gradient descent
1.1 GD
- random choose θ0
- θi = θi-1 - η∇L(θi-1)
这个式子,我之前一直没留意,η∇L(θi-1),这里是斜率越高,也即坡越陡 w 更新的步伐越大,斜率越小,坡越缓,w 更新的越慢,这个特别像是从山坡上滚下来的速度。
Tuning Learning Rate
步进要注意调整,但是我该怎么看到 Learning rate 对于 loss 的影响呢?
. ^loss . | / 步幅超级大,飞到对面山上去了 . | / . |/ . |\ . | ------------ 步幅太大卡住了 . +-------------> 调整次数
要学会通过看 Loss-updateNum 曲线来判断 learning rate 是否合适。所以做 gradient 时一定要把这个图画出来。
但是要调整 learning rate 真的很麻烦,有没有办法自动调整呢? Adaptive learning rate 通常,learning rate 会随着 update 次数,越来越小。
popular and simple idea reduce the learning rate by some factor every few epochs
eg: 1/t decay: ηt = η0/√t+1
这样 learning rate 会随着时间越来越小,但是这样往往不够动态。
1.2 AdaGrad
原来我们有很多参数,但是我们是对参数的 gradient 整体 *η我们希望给不同的参数不同的学习率,该怎么做呢?
Adagrad = 1/t decay + GD w - 表示某个具体的参数 gt - 表示某个具体参数对 Loss-fn 的偏微分σt - root mean square of all previous(include current time) derivatives of w
σt = √Σg2/(t+1)
ηt = η0/√t+1
wt+1 = wt - ηtgt/σt = wt - η0gt/√Σg2 = wt - η'gt
Adagrad 在后来是非常非常慢的,慢的可怕,因为他是 t-decay 的。
>>> decay ----------------------------------------- 上次遇到 decay 是 L2-regular 他是 weight-decay 为甚么叫做 weight-decay, 因为把带有 L2-regular 的式子用微分(GD)处理可以发现,L2-regular 会按比例 缩小 w ,所以是 weight-decay -----------------------------------------
1.2.1 adgrad 与 GD 的区别:
wt+1 = wt - η0gt/√Σg^2
跟 GD 不同,GD 是坡越陡峭 w 更新的越快。但是 adagrad 似乎有点矛盾,乘以 gt,除以 gt 的 root sum square。一个加速更新,一个减速更新。所以这里 adagrad 不是根据·「坡的陡峭程度」来调整 w 的更新步伐。而是根据 ·「坡度的反差」 来决定 w 的更新步伐。
为什么用 ·「坡度的反差」比·「坡度的大小」更好。我们希望这个步进的次数越少越好。最好就一步到位。只更新一步就到谷底。best step = 一次微分/二次微分
1.3 Stochastic Gradient Descent
optimizer 应该是 独立于具体的 loss-fn 的。这里仅仅用 regression 的 loss-fn 作为例子。
L(regreresidue) = sum square all residue w = w - η∇L
他考虑的是每一个点的 residue 的平方,然后取和。 而 SGD 不是这么做,他的 loss-fn 略做变化: 他不是看完所有的点的 residual 然后作处理, 而是看一个点就得到一个 L,update 一次 w ,然后再看下一个点得到一个 L,update 一次 w。
L1(regre_residue) = square one residue w = w - η∇L L2(regre_residue) = square one residue w = w - η∇L L3(regre_residue) = square one residue w = w - η∇L L4(regre_residue) = square one residue w = w - η∇L L5(regre_residue) = square one residue w = w - η∇L
如果只有 20 个点,那么每个点都算一遍 residual 的平方没什么问题。如果是有 20w 个点呢?要看完才更新是不是太慢了。
这是 SGD 就很好用,可以选择自己的更新次数。比如 1w 次更新。SGD 更灵活。
1.4 GD SGD ADA Relationship
·「总结」 GD 的每一个 wi 都用【相同】的 ηi GD 的每一个 wi 都用【不同】的 ηi ===> Adagrad GD 的每一个样本分开做 update ===> SGD
1.5 Feature scaling
两个 input feature,如果两个 feature 的分布很不一样的话,就建议把他们通过某种方法做成一样的,比如
所有样本的第一个特征值的分布是 [-100, 100] 所有样本的第二个特征值的分布是 [-10, 10]
这样就建议对他们做 feature scaling : make different feature have same scaling.
为什么要做 feature saling ?
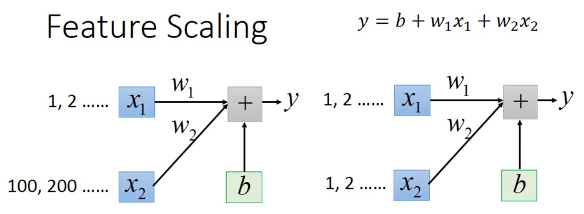
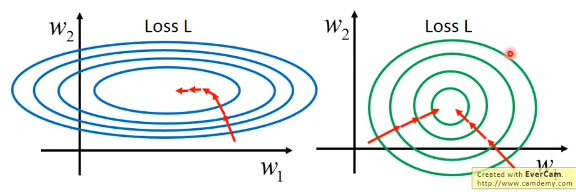
做 feature scaling 的本质就是让不同参数对 loss-fn 的影响尽量一致—形成圆形
- SGD,GD,adagrad 中只有 adagrad 能处理椭圆的情况
- 因为椭圆的优化路线不是直接朝着椭圆中心,很明显红线走了弯路而圆形的优化路线是直接朝着圆心走,红线很直。
所以很明显圆形可以更快的到达谷底,而且可以使用更多的优化方法,可选择范围广。那怎么做 feature scaling 呢? 如下图示 x1 x2 x3 … xr … xR 都是样本点
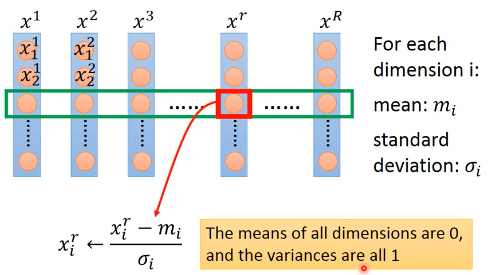
1.6 Newton method
GD 的本质是考虑了 Taylor Series 的一次式。如果考虑他的二次式就是 Newton method.
但是同样代价是,你需要算 二次微分,海森矩阵,海参矩阵的逆矩阵如果参数很少还勉强可以,如果是 Deep learning 那种级别的参数运算效率是无法承受的。
1.7 More limitation of Gradient Descent
- stuck at local minima
- stuck at saddle point
- very slow at the plateau
注意图中的这种 saddle point,以前没见到过,需要加深对 saddle point 的理解
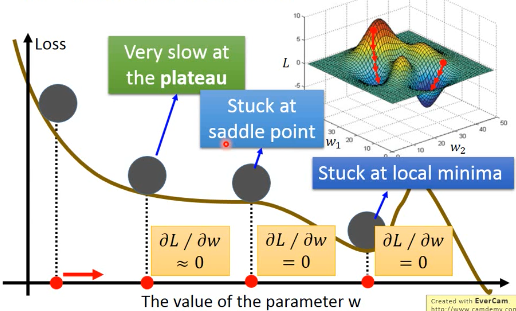
我们在做 GD 的时候,并不是真的得到 gradient=0 的时候才停下,而是到某个很小的梯度值就停止了。但是这样的点,从上图中也可以看出他可能还处在高原上,根本不低,而且离 local minima 还很远,更别说 global minima 了。