lec-04 Classification
Table of Contents
1 Classification
如果用 regression 直接做 classification,用+1/-1 来表示结果。
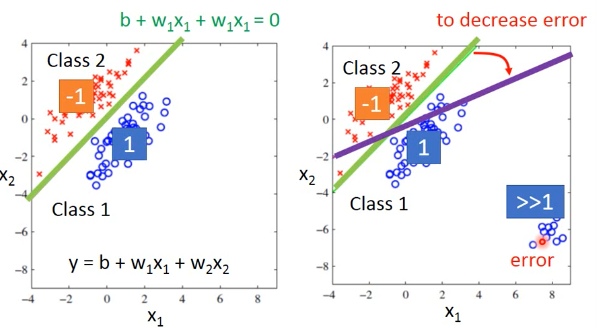
这会造成·「y 值太大的那些点会被照顾太多」,这样分界面会从我们希望的绿色转向紫色。这是由于 regression 的 loss-fn.并不适合做 classification。也就是我们·「看待 residue」的方式要改变,也就是说衡量模型好坏的标准要改变。
传统的方法有:perceptron,SVM
这里介绍一种基于概率分布的观点:
1.1 Gaussian Distribution
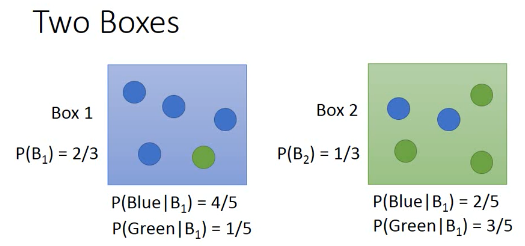
想想 bayes 定理:以 P(A and B) 的交换律为基础而形成的定理。
- 已经知道从 A/B 各自抽取的概率
- 已经知道 A/B 各自包含蓝绿球的比例
- ==> 问抽一个蓝球,来自与 A 的概率
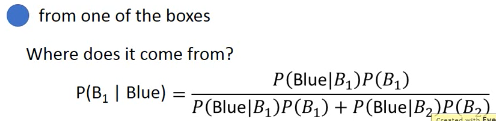
如果把盒子换成分类的话:
- 已经知道从 A/B 各自抽取的概率 | 1. 已经知道 A/B 类型各自的占比
- 已经知道 A/B 各自包含蓝绿球的比例 | 2. 已经知道某个样本点是 A/B 的概率
- ==> 问抽一个蓝球,来自与 A 的概率 | 3. ===> 这个样本点是 A 类型的概率
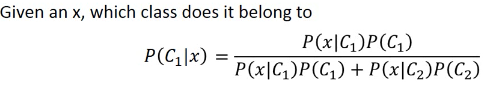
想得到(3),就得显得道 (1)(2), 所以我们想通过 trainingdata 来获得.
. Generative Model . . 这种想法很有用,叫做 Generative Model . 你可以通过这个模型 Generate 一个 x,P(x),如果你知道 x 的 distribution,你就可以 . 产生 x。
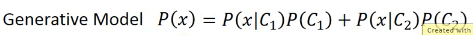
Prior Probability 算步骤(1): P(C1) P(C2) 直接通过 labeled data 来计算所有样本中 C1 类,C2 类各自的占比 Probability from Class 这个比较麻烦,新来的一个 testpoint:x,他不在 trainingdata 的 C1 样本中。我怎么判断他是出自 C1 的概率呢?换种思路:trainingdata 的所有 C1 样本也是从某个更大的 C1'样本集合中抽取出来的而新来的 testpoint 就是出自 C1'. 我们假设 C1 是通过 Gaussian distribution 从 C1'中抽取出来的。所以如果我能得到这个 Gaussian distribution,我就能得到 P(x|C1')
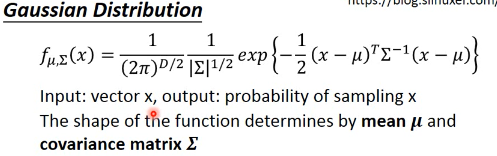
这是高斯分布的概率密度公式,他正比与高斯分布的概率值有两个变数,Σ μ, 同样的 x,如果带入不同的 Σ μ, 就会产生不同的高斯分布如果 trainingdata 中所有的 C1 点都是通过某个 Σ μ 抽取出来的,那么我就可以通过 trainingdata 中的所有 C1 点来得到 Σ μ, 得到这个高斯分布我再带入 testpoint:x, 就可以得到 P(x|C1')~~P(x|C1)
可以看出,如果 x 离 μ 越近这个 P(x|C1')的概率就越高,反之很低。
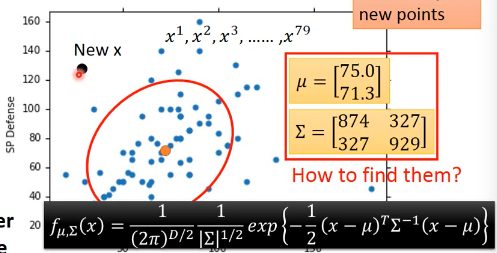
下面的问题是如何找到 Σ μ
1.2 Maximum Likelihood
任何一种高斯分布都·「有可能」抽取出训练集的 C1 点。只是有些地方概率高,有些地方概率低,但没有一个地方概率是 0。
但是不同的高斯分布抽取出 C1 的概率不一样。
从中选取 likelihood 最大的那个高斯分布 Likelihood 公式:
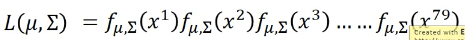
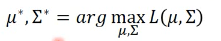
求微分就可以解答
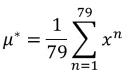
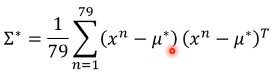
然后算出每一种 trainingdata 的分类所对应的 maximum likehood Gaussian
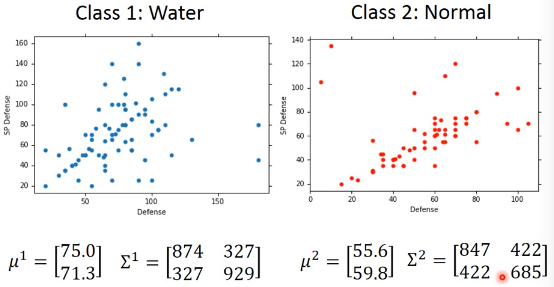
算法步骤 1. 直接通过 labeled data 来计算所有样本中 C1 类,C2 类各自的占比 Probability from Class P(x|C1) = Gaussian(μ1,Σ1) P(x|C2) = Gaussian(μ2,Σ2) 2. Now we can do classification P(C1|x) = P(x|C1)P(C1)/P(x) = P(x|C1)P(C1)/(x in C1) or (x in C2) = P(x|C1)P(C1)/(P(x|C1)P(C1) + P(x|C2)P(C2)) if P(C1|x) > 0.5 , x ∈ C1
+----------------------+--------------------------+ | | | | +-----------------+----------------+ | | | P(x|c1) | p(x|c2) | | | | | | | | +-----------------+----------------+ | | | | | p(c1) | P(c2) | +----------------------+--------------------------+
1.3 Modifying Model
make Covariance Matrix Σ same Σ 是跟 input 量成正比的,当 input 太大的时候,Σ会增长的很快。所以让他们一样,这样减少参数,避免 overfitting
modify Gaussian
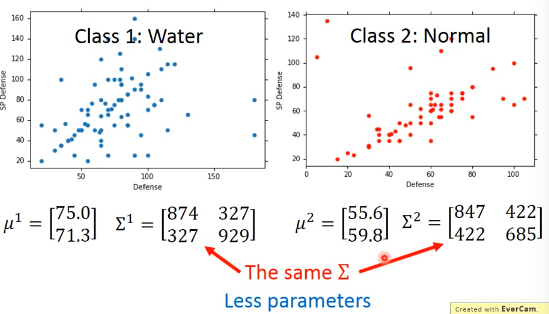
modify Maximumu likelihood
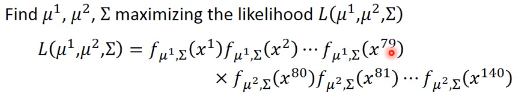
微分这个 maximum liklihood 公式,得到最好的 Σ μ: μ1' = average of C1 μ2' = average of C2 Σ' = C1 比例 × Σ1 + C2 比例 × Σ2 其中 Σ1Σ2 是用最原始的方法得到的两个 covariance matrix
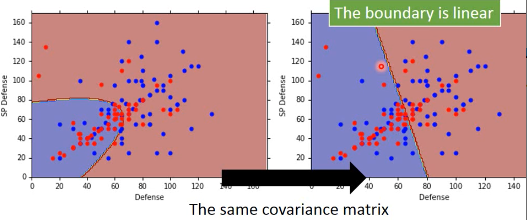
可以看到,当我们强制 covariance 相等时通过 微分最大似然函数 得到的两个概率分布然后再通过 post-probability 算出的 boundary 是线性的
·「总结」
1.3.1 tree steps
Funcion Set -> Post probability of different P(x|c1) and P(x|c2)

Goodness of a function -> Σμ make Likelihood is larger

Find the best -> a analogy result 注意这个模型不像其他模型需要通过·「循环优化」,他是可以通过微分直接求出最优解
1.4 Many other Probability Distribution
人来决定这个 tradoff,复杂的概率模型 bias 就小,variance 就大。
1.4.1 假设 input 多个 feature 相互独立来简化概率模型 :Naive Bayes:
- 从向量上看,没有任何关系就是,两个向量的相似度为 0,那么他们应该是·「垂直的」。
- 从概率上看,没有任何关系就是·「独立事件」。
如果我们假设 inputpoint 的各个维度(feature)之间没有任何关系:

那么,一个 K 维度高斯,就被转换成 K 个一维度高斯的乘积。这大大简化了 K 维度高斯的 Σμ 的计算。但是这么做是有风险的,有可能损失了·「特征间关系」这一信息。让模型没法对·「正确的特征做强有力的映射」。最后会出现 underfitting。
这种·「独立性假设」化简概率模型然后来做分类的方法就叫做 Naive Bayes Classifier
1.4.2 根据问题目标来决定概率模型:
- 两个 feature,Bernoulli Distribution
1.5 Dive into Posterior Probability Sigmoid
1.5.1 引入 sigmoind
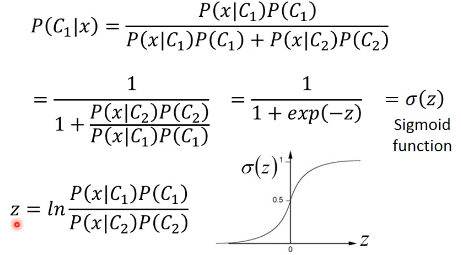
post-probability ===> Sigmoid function P(C1|x) = σ(z)
1.5.2 殊途同归:统一向量模型和概率模型
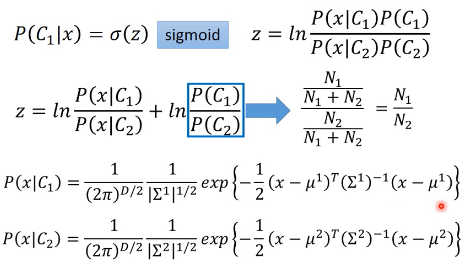


如果我们按照之前的假设: Σ1 = Σ2 = Σ

之前已经对比过,post-probability 就是 function set 可以看到,最后的 post-probability 被化简成一个 ·「线性组合的 sigmoid 激活」这也解释了,为什么之前做了 ·「假设协方差矩阵相等」这个让步之后,得到的 boundary 是线性的。
既然,最终都可以通过 ·「假设协方差矩阵相等」这个让步,把复杂的·「概率模型」转换为一个·「向量线性组合模型」,为什么不直接找这个向量模型呢?详情见下一节课