UP | HOME

lec-09 Recipe of Deep Learning

Table of Contents

1 Recipe of Deep Learning

Deep learning, 虽然参数很多，但确实不容易 overfitting。 K-NN, DecisionTree 训练集上一做就是 100%正确，这才是 overfitting。 DL 在训练集上就不太容易获得好的结果，所以即便在测试集上也不好，这个也不算是 overfitting

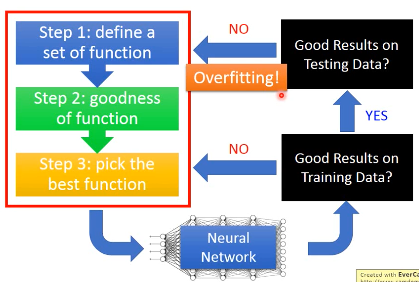
screenshot_2017-06-10_12-56-40.png

如果出现 overfitting，调整了这三个训练步骤之后，还是要再检查一遍训练集是否足够好。

1.1 Do not always blame Overfitting

下图的 56-layer 并没有 overfitting，因为训练集和测试集都是这样的表现

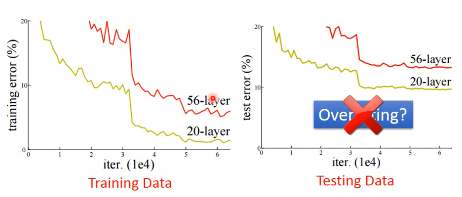
screenshot_2017-06-10_12-59-26.png

在做 DL 的时候，有太多太多的可能性让你的结果是不好的：

  1. local minimum
  2. saddle point
  3. plateau(高原:低斜率，但高)

这个并不是 overfitting，也不是 underfitting，就是没有 train 好。

1.2 「针对训练 or 测试」

screenshot_2017-06-10_13-07-05.png

在 DL 中有两个问题：Testing 不好 和 Training 不好。 eg. Dropout for testing data ONLY

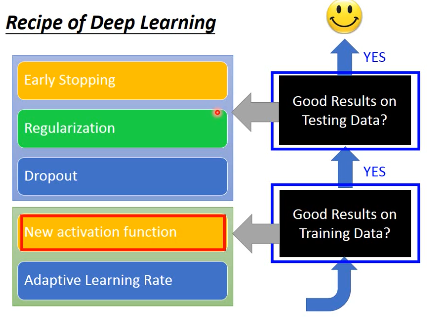
screenshot_2017-06-10_13-08-49.png

2 Bad results on Training Data

2.0.1 New Activation Function

如果是训练集上效果不好，有可能是 function-set 不行，也就是 net structure 没设计好。比如 激活函数不好

2.0.2 Hard to get the power of Deep

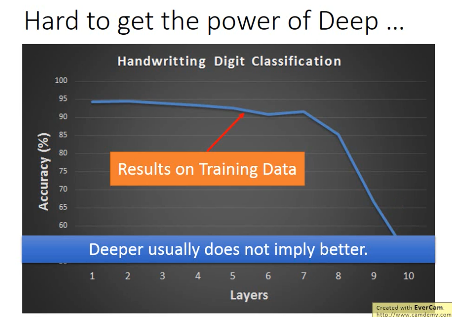
screenshot_2017-06-10_13-11-34.png

2.0.3 为什么 layer 越多，正确率不增反降？

一个可能的原因是：梯度消失 and 梯度爆炸

2.1 Vanishing Gradient Problem

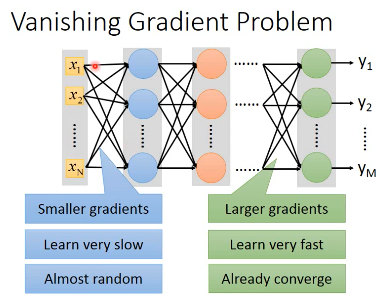
screenshot_2017-06-10_14-52-06.png 

                   input layer 附近的参数 w 对于
                 /  loss function 的微分会非常小.
                 |             |
                 |             |
                 |             | 如果设定相同的 learning
                 |             | rate with下面
-----------      |             |
w near input     |             v
layer just       |     参数 w update 非常慢
random; while    |
w near output   <|
has converged    |  output layer 附近的参数 w 对于
-----------      |  loss function 的微分会非常大.
                 |              |
                 |              |
                 |              | 如果设定相同的 learning
                 |              | rate with上面
                 |              |
                 \              v
                        参数 w update 非常快

2.1.1 sigmoid 会衰减变化量

backpropagtion 的意义是用梯度，也就是微分。求的是某一个 w 的增加量对于 loss-fn(cross-entropy)的变化量的比值：

\(\frac{\partial{C}}{\partial{w}} = \frac{\bigtriangleup{C}}{\bigtriangleup{w}}\)

但是由于 sigmoid 函数对于·「差距的衰减」作用， 如下图所示:

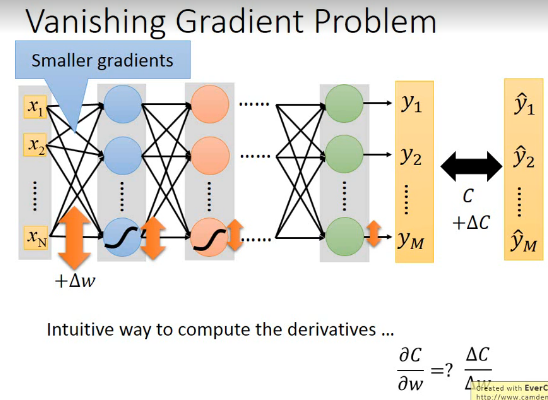
screenshot_2018-07-20_02-48-23.png

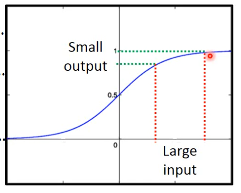
screenshot_2017-06-10_14-49-54.png

导致越靠近 input-layer 的 w 的变化量: \(\bigtriangleup{w}\) 所带来的计算结果(will contribute to finall loss)每经过一个神经元(sigmoid)都会变小，所以随着经过的 layer 越来越多，更新这些 w 对于 output layer 的影响越来越小，所以最后 output:y' 几乎是不变的。所以 C 也几乎是不变的 — \(\bigtriangleup{C}\) 几乎为 0。 所以

for w near input layer:

∂C/∂w = every SMALL

then w near input layer update very small each time, for a long run-time it's still random

反之靠近 output-layer 的 w 的变化量:∂w 由于经过的神经元很少，衰减很少，对于 output-layer 的影响就大，∂C 就大。所以

for w near output layer:

∂C/∂w = every LARGE

then w near output layer update very large each time, for a short run-time it's converged, but it converged based on the random w near input layer, although converged, lead to bad prediction.

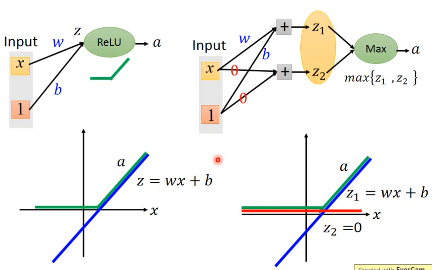
2.1.2 如何解决：更换激活函数为 ReLU

z - input a - output

screenshot_2017-06-10_15-05-10.png

  1. 对于那些输出为 0 的神经元，根本不会影响最后一层的输出

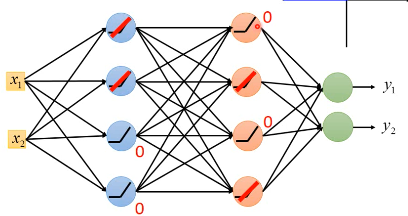
screenshot_2017-06-10_15-19-28.png

可以直接拿掉

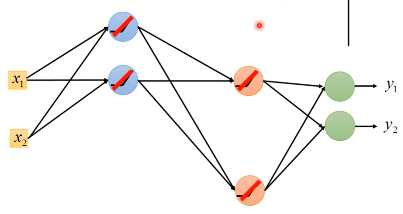
screenshot_2017-06-10_15-19-44.png

  1. 对于那些输出不为零的神经元，整个构成一个瘦长的线性网络

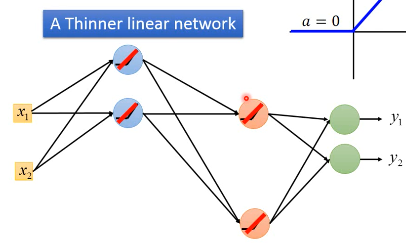screenshot_2017-06-10_15-20-57.png 这里就不存在·「差距衰减」的问题，但是还有两个问题：

  1. 我们并不喜欢 linear network 这种模型太弱了。
  2. ReLU 没办法微分。

其实这两个问题都不是问题：

  1. 联合起来当 x 取值较大的时候并不是 linear network
  2. ReLU 只在输入为 0 的位置不可微分，但很少遇到需要这里的微分。

2.1.3 ReLU - variants

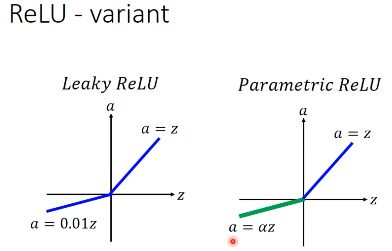
screenshot_2017-06-10_15-28-58.png

Leaky ReLU and Parametric ReLU

激活函数不一定要事先指定 ===> 对 ReLU 再次进化

2.1.4 ReLU - advanced: Maxout

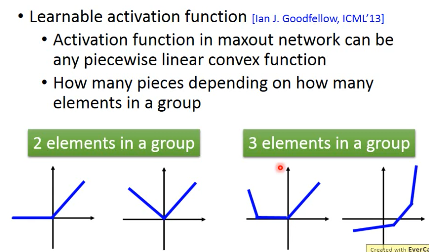
Learnable activation function 激活函数是自动学出来的

  1. group

哪些 value 会 group 在一起是事先决定的。每个 group 内的元素个数可以随便选。

  1. 选 max 作为输出

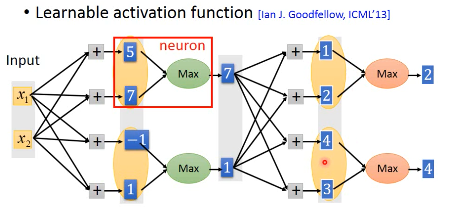
screenshot_2017-06-10_15-33-51.png

就不加 activate-function 了。 ReLU is a special cases of Maxout

screenshot_2017-06-10_15-37-50.png

2.1.5 Maxout is more powerful

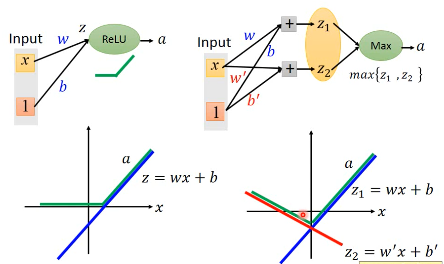
screenshot_2017-06-10_15-39-03.png

Learnable activation function

screenshot_2017-06-10_15-40-31.png

2.1.6 How to train Maxout network

Maxout 没法微分，这个怎么用 Gradient 来训练呢？

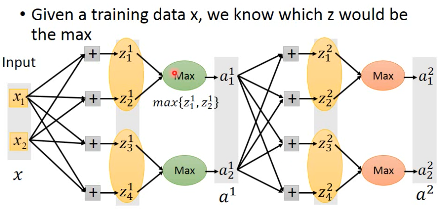
screenshot_2017-06-10_15-44-11.png

没有接到的部分，就可以直接拿掉，当你一个输入进来，之后其实他就是一个细长的 linear network, 你根本不需要考虑 Maxout 的拐点没法微分的问题

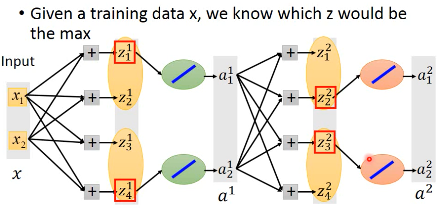
screenshot_2017-06-10_15-44-56.png

所以你需要 train 的不是 Maxout，而是这个 linearNetwork

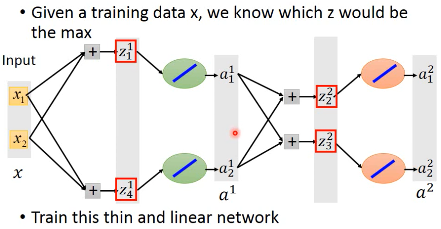
screenshot_2017-06-10_15-46-04.png

但是，好像那些被删除的链接的 weight 怎么办？他们没有被 train

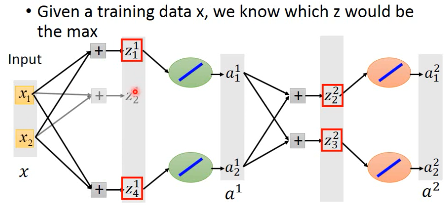
screenshot_2017-06-10_15-49-11.png

当你给他不同的输入时（x）,maxout 会选择各种不同的链接，所以概率上每一个连线(weight)是都会被 train 到的。 

Maxout 和 Max-pooling(CNN)是完全一样的。

2.2 Adaptive Learning Rate: RMSProp

Error surface can be very complex when training NN即便在同一个方向上 learning rate 也必须快速的变动(adagrad 在某一个方向(dimension)的 learningrate 是固定的)

review grad (下图中去掉根号部分就是 gradient-descent)

review AdaGrad(dimension-wise + 2nd derivative)

学习率从原来的·「除以 1」变成·「除以平方和开根号」

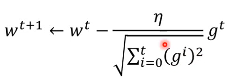
screenshot_2017-06-10_16-07-32.png

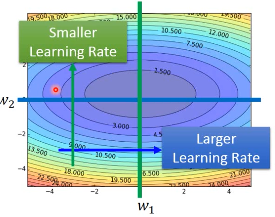
screenshot_2017-06-10_16-11-34.png

Error surface can be very complex when training NN即便在同一个方向上 learning rate 也必须快速的变动(adagrad 在某一个方向(dimension)的 learningrate 是固定的)

screenshot_2017-06-10_16-13-37.png

Adagrad 进阶版： 

RMSProp根号里面引入·「gt 的可调节权重」--- α手动设置，一般设置个 0.9 之类的。

α小---倾向于相信新的 gradient 告诉你的曲线的平滑或陡峭的程度。
α大---倾向于相信以前的 gradients
adagrad RMSProp
Root Mean Square RMS with previous gradients being _decayed

screenshot_2017-06-10_16-20-52.png

2.2.1 Hard to find optimal network parameters

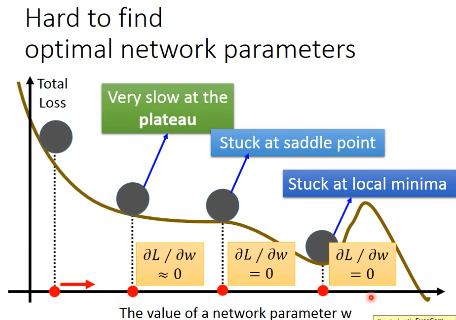
screenshot_2017-06-10_16-22-42.png

  1. Very slow at the plateau
  2. Stuck at saddle point
  3. Stuck at local minima

不用太担心 local-minimum 的问题，其实在 error-surface 上没有太多 local-minimum 的情况。因为如果你是 local-minimum 你就必须在每一个 dimension 都是如上图的形状，假设某一个参数 w 相对 Loss-fn 是这种形状的概率是 p，因为 NN 参数非常多，那么 1000 个 w 同时出现这种形状的概率是 p1000 参数越多，local-minimum 出现的概率越低。

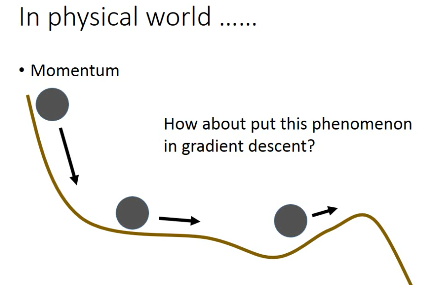
screenshot_2017-06-10_16-27-56.png

将惯性引入 GradientDescent

2.2.2 Momentum

Review: Vanilla Gradient Descent

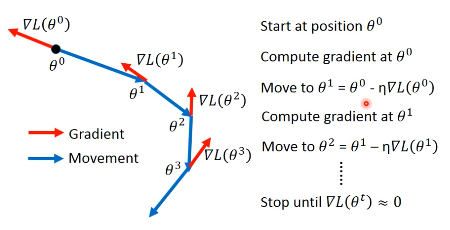
screenshot_2017-06-10_16-29-02.png

加入惯性 movement 之后

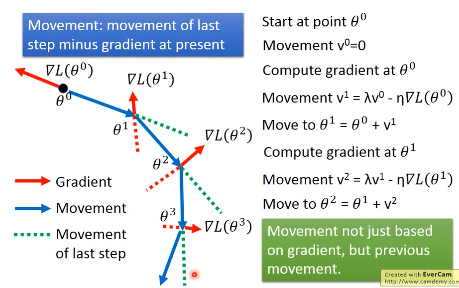
screenshot_2017-06-10_16-45-42.png

Movement: movement of last step minus gradient at present 引入·「惯性的权重参数」— λ, λ大就代表更看重惯性，λ小代表更看重当前的 Gradient

GradientDescent Momentum(v)
w2 = w1 + (-ηg2) v2 = λv1 + (-ηg2)
  w2 = w1 + v2
  v0 = 0

vi is actually the weighted sum of all the previous gradient:

∇L(θ0),∇L(θ1),∇L(θ2),…,∇L(θi-1)

v0 = 0 v1 = -η∇L(θ0) v2 = -λη∇L(θ0) - η∇L(θ1) …

越之前的 gradient 的 weight 越小

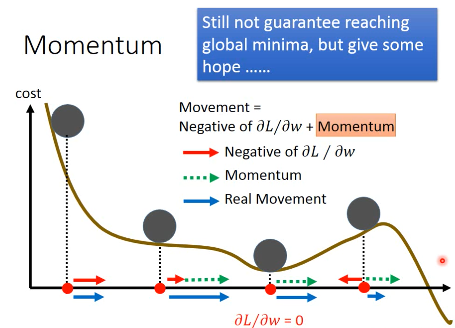
screenshot_2017-06-10_16-54-26.png

2.2.3 Adam(= RMSProp + Momentum)

adagrad RMSProp
Root Mean Square RMS with previous gradients being _decayed

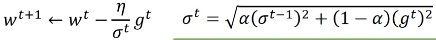
screenshot_2017-06-10_16-57-37.png

GradientDescent Momentum(v)
w2 = w1 + (-ηg2) v2 = λv1 + (-ηg2)
  w2 = w1 + v2
  v0 = 0

screenshot_2017-06-10_17-01-44.png

3 Bad results on Testing Data

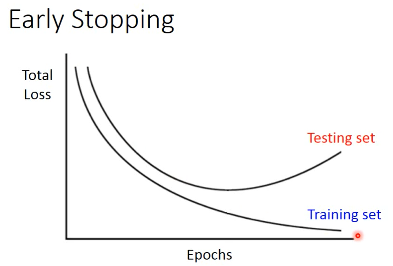
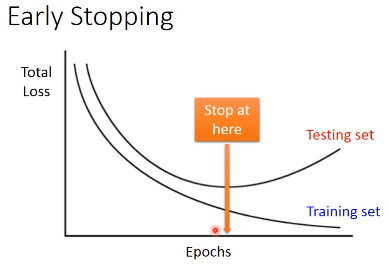
3.1 Early Stopping

Early Stopping 和 Regularization 是普适的做法，并不只针对 NN, Droput 是针对 NN 的做法

screenshot_2017-06-10_17-08-29.png

screenshot_2017-06-10_17-09-00.png

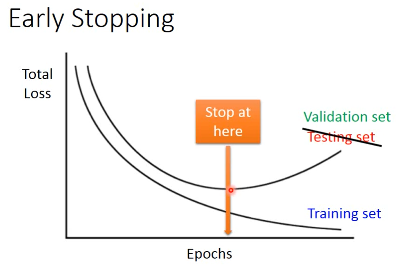
注意，因为 Testing set 是未来的未知数据，所以这里只能通过 验证集 来模拟

screenshot_2017-06-10_17-10-19.png

3.2 Regularization

New loss function to be minimized:

  • Find a set of weight not only minimized original cost but also close to zero

3.2.1 L2 Regularization

screenshot_2017-06-10_17-12-09.png Regularization: usually not consider biases 之前讲过 regularization 是为了让函数更平滑，但 ‘b’ 通常是跟函数平滑程度没有关系的。

screenshot_2017-06-10_17-14-47.png

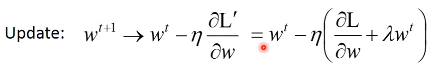
screenshot_2017-06-10_17-14-57.png

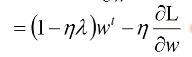
screenshot_2017-06-10_17-15-20.png

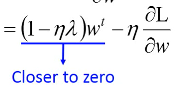
screenshot_2017-06-10_17-15-37.png

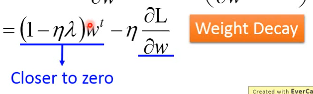
screenshot_2017-06-10_17-20-43.png

Closer to zero, 离 0 越来越近因为 η,λ 都很小，1 - η*λ = 0.99 所以每次做更新，都是把 wt 先乘以 0.99 这样某一个前面的 w， 比如 w1 因为每次都要 *0.99,所以会越来越靠近 0

3.2.2 L1 Regularization

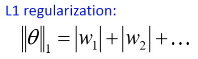
screenshot_2017-06-10_17-26-14.png

screenshot_2017-06-10_17-28-08.png

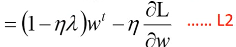
screenshot_2017-06-10_17-28-54.png

3.2.3 L1 和 L2 有什么不同

一样的，always decay ==> always delete 在 L2-regularization 中，如果出现很·「大」的 w，由于是·「按比例」缩放所以 w 会很·「快」的变小。在 L1-regularization 中，如果出现很·「大」的 w，由于是·「按量」缩放所以 w 会很·「慢」的变小。

在 L2-regularization 中，如果出现很·「小」的 w，由于是·「按比例」缩放所以 w 会很·「慢」的变小。在 L1-regularization 中，如果出现很·「小」的 w，由于是·「按量」缩放所以 w 会很·「快」的变小。

所以总体来说，L1 产生的 w 矩阵会比较·「稀疏」，既有很大的 w，也有很多（=0）的 w 所以总体来说，L2 产生的 w 矩阵会比较·「稠密」，大部分 w 都不大或者接近 0（！=0）

CNN 里面想产生 sparse 的结果的 image，所以用 L1

TODO: https://www.youtube.com/watch?v=sO4ZirJh9ds&index=64&t=109s&list=WL 这个教程很好，似乎 regularization 引出了 convex optimization 的某些概念

3.2.4 Regularization - weight decay

跟人脑的机制很像。

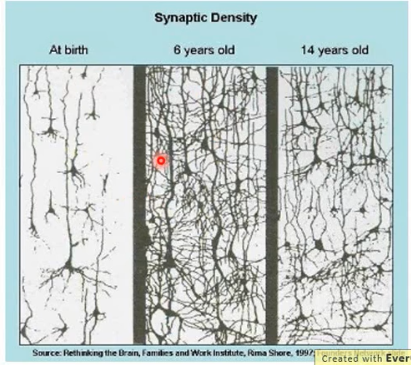
screenshot_2017-06-10_17-38-59.png

6 岁初识世界，很多都感兴趣，会建立大量的神经连接。但是到 14 岁，由于很多神经元都用不到，也有很多事情不去玩了(类比没用的 weight 不去 update，就会慢慢 decay 到 0)所以很多神经元连接就消失了。

3.3 Regularization vs. Early stopping

虽然在 NN 中 Regularization 有些帮助，但是帮助不是很大，没有像 SVM 这么依赖 regularization。

我们一般给 NN 的参数初始值都是很小的，或者接近于 0 的。我们下面做的事情就是让这些参数离 0 越来越远。 

Early Stopping 是减少·「离 0 的次数」
Regularization 是减少·「离 0 的步幅」

总体来说都是让参数·「不要离 0 太远」

3.4 Dropout

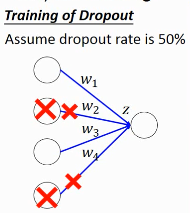
3.4.1 Traning

===== 在每一次更新 w 之前，对 layer 做 sampling—决定要不要丢掉

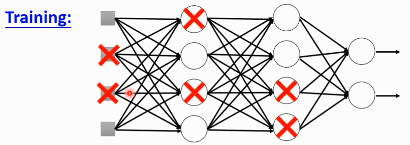
screenshot_2017-06-10_17-42-15.png

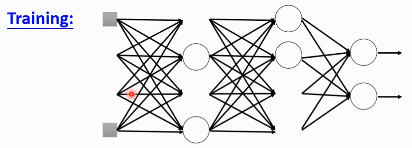
screenshot_2017-06-10_17-42-43.png

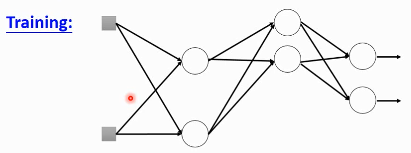
screenshot_2017-06-10_17-42-58.png

这样每一次 update 之前都要做一次 sampling，都改变了 structure, 所以你每一次做 update 的 w 都不一样，要 traing 的 NN 也不一样。

Each time before updating the parameters

  1. Each neuron has p% to dropout ===> The structure of the NN is changed
  2. Using the new NN for training
  3. For each mini-batch, we resampling the dropout neurons

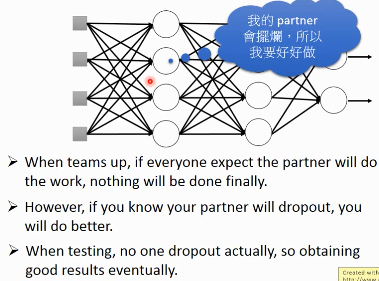
在训练的时候，很明显 dropout 削弱了模型的能力，所以使用 dropout 之后，训练效果会变差所以，一定要确保在使用 dropout 之前，是训练集效果很好，测试集效果不好，才能使用。如果 训练集 本身就不好，那么 dropout 只会让训练集越来越差。

3.4.2 Testing

=====

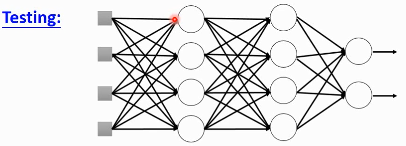
screenshot_2017-06-10_17-49-33.png

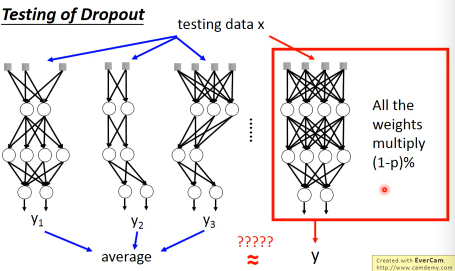
No dropout:

  1. if the dropout rate at training is p%, all weights times (1-p)%
  2. assume that the dropout rate is 50%, if a weight w = 1 at training, set w = 0.5 for testing

3.4.3 Why dropout work

– Intuition Reason

screenshot_2017-06-10_17-52-55.png

screenshot_2017-06-10_17-53-02.png

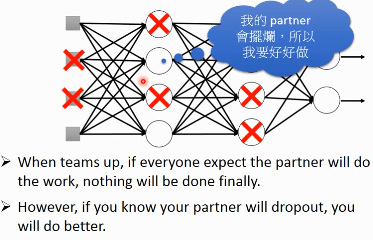
screenshot_2017-06-10_17-53-57.png

screenshot_2017-06-10_17-54-12.png

3.4.4 Why multiply (1-p)%

different weight in training and tesing

screenshot_2017-06-10_18-04-40.png

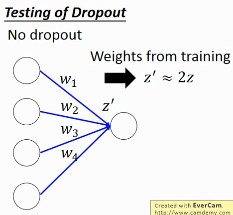
screenshot_2017-06-10_18-05-09.png

如果不乘以(1-p)%, 那么 training 和 testing 的输出不一致，这样 testing 反而会不好所以需要乘以(1-p)% 来大概的保证结果是一致的。

screenshot_2017-06-10_18-04-53.png

一个更学术的理由：

3.4.5 Dropout is a kind of ensemble

Ensemble Learning 在比赛中很常用，

3.4.6 Ensemble Learning 为什么 work

之前讨论过 error 来自于两个方面：bias , variance

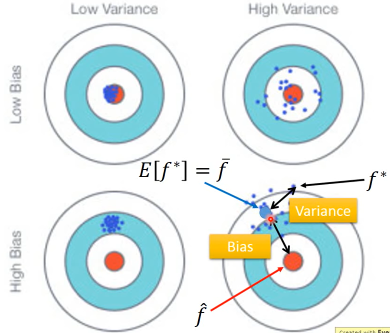
screenshot_2017-06-10_18-11-41.png

如果模型能力强：bias 造成的 error 小，variance 造成的 error 大如果模型能力弱：bias 造成的 error 大，variance 造成的 error 小

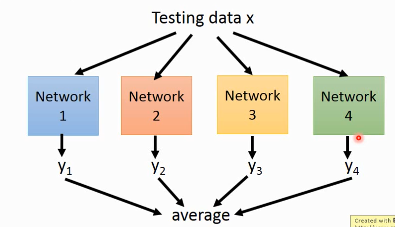
所以如果有很多能力较弱的 model，平均起来看，可以消去 bias 造成的 error 所以如果有很多能力较强的 model，平均起来看，可以消去 variance 造成的 error

而且还可以利用 parallel 来 traing 各自的 model

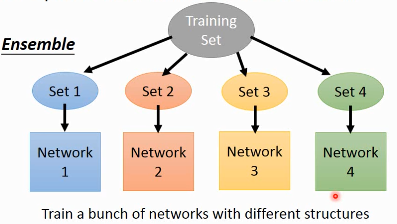
screenshot_2017-06-10_18-14-37.png

注意这里是把 training data 分成几份，所以每个子训练集都不一样

screenshot_2017-06-10_18-15-59.png

RandomForest 就是实践这种精神的一种方法，每一个 DecisionTree 随便 train 一下都会 overfitting，但是当很多 DecisionTree 放在一起的时候，就不容易 overfitting

3.4.7 Training of Dropout

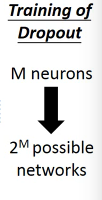
======================== Dropout will produce many different structure of NN

因为每个 minibatch 在进行 update 的时候，都会做一次 sampling 产生出不同的 structure 因为这种 sampling 会作用在所有的 神经元，当然也包括 input-layer，所以，每次的输入也被 sampling 成不同的‘输入’，所以完全可以看成是上面的 ensamble learning 的重现。

different input + different structure

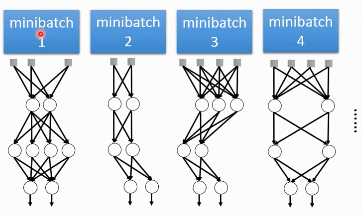
screenshot_2017-06-10_18-18-12.png

screenshot_2017-06-10_18-22-28.png

  • using one mini-batch to train one network
  • some parameters in the network are shared

虽然一个 network 使用 一个 mini-batch 来 train 但是某一个神经元，有可能出现在好几个 mini-batch 中，所以这个神经元就是被·「好几个 mini-batch」train 的。

3.4.8 Testing of Dropout

====================== 所以，根据 ensamble leanring，应该这么做，但是 sampling 是随机的，这样做很不现实，不效率

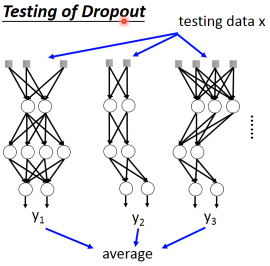
screenshot_2017-06-10_18-26-21.png

所以采用一种近似的方法：weight*(1-p)%

screenshot_2017-06-10_18-28-44.png

为什么可以‘约等于’呢？举例说明

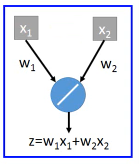
screenshot_2017-06-10_18-29-43.png

Dropout(ensamble) will produce:

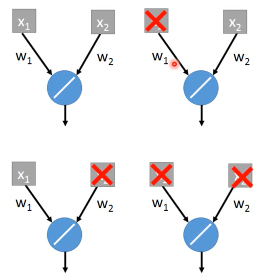
screenshot_2017-06-10_18-30-19.png

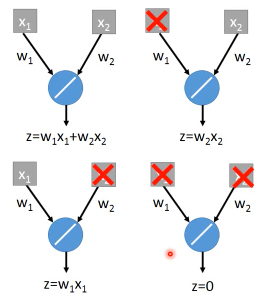
screenshot_2017-06-10_18-31-00.png

ensamble will average the all z: (w1x1 + w2x2 + w2x2 + w1x1 + 0)/4 = 1/2w1x1 + 1/2w2x2

dropout will weights*(1-p)% :

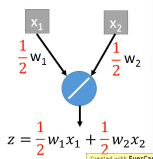
screenshot_2017-06-10_18-31-41.png

ensamble average and dropout weight*(1-p)% will be equall

但是很明显，不会所有的 dropout 方法最后都和 ensamble 方法的结果相同。 只有 linear 的 NN 才有可能产生这种结果。

所以有些人

3.4.9 获得了这样的灵感

既然只有 lienar nn 才能让 dropout 产生和 ensamble 完全相同的结果。那我干脆就使用 linear NN 效果肯定更好。

比如使用激活函数为 ReLU or Maxout,这样的 NN 在使用 dropout 之后效果肯定非常好。

实际上确实如此。以为内 ReLU 和 Maxout 的激活函数跟 linear-fn 很相近

Date: 2017-06-06

Author: yiddi

Created: 2018-08-12 日 14:55

Validate