lec-13 Unsuprevised Learning
Table of Contents
- 1. Unsuprevised Learning
- 1.1. 无监督学习分成两种:化繁为简和无中生有
- 1.2. Clustering(一个数据点对应一个簇)
- 1.3. Distributed Representation(一个数据点对应多个簇)
- 1.4. Dimension Reduction
- 1.5. PCA: principle component analysis
- 1.6. PCA 怎么做呢?
- 1.7. 看待 PCA 的另一个视角
- 1.8. PCA 的弱点
- 1.9. PCA 例子
- 1.10. MF: matrix factorization
- 1.11. LDA: linear discriminent analysis
- 1.12. 很多的 Dimension reduction 方法
- 1.13. Demystifying Dimensionality Reduction
1 Unsuprevised Learning
outline:
- Clustering
- Distributed Representation
- Dimension Reduction
- PCA
- PCA decorrelation
- PCA another point of view
- weakness of PCA
- PCA pokemon
- PCA MNIST
- PCA Face
- what happens to PCA
- NMF on MNIST
- NMF on Face
- Matrix Factorization
- More about MF
- Matrix for Topic analysis
- More Related Approaches not introduced
1.1 无监督学习分成两种:化繁为简和无中生有
1.1.1 化繁为简 clustering and Dimension reduction
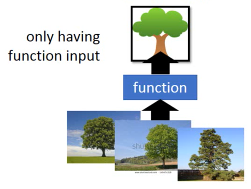 clustering and Dimension reduction
各种各样的树 —> 聚类成‘一个树’复杂的 —> 简单的
clustering and Dimension reduction
各种各样的树 —> 聚类成‘一个树’复杂的 —> 简单的
数据一般不像监督时学习,需要 label。非监督学习的训练集,只需要给 x,不需要给 y(label)
这个特别类似·「降维度」和·「特征提取」,因为我们也不知道 label 是什么
1.1.2 无中生有 Generation
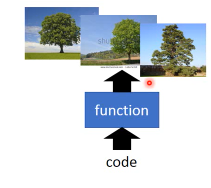 Generation
逆向,给一个简单的 code,产生多种不同的树
Generation
逆向,给一个简单的 code,产生多种不同的树
1.2 Clustering(一个数据点对应一个簇)

到底需要几个 cluster?这个就跟 NN 要几层一样,需要灵感跟经验
1.2.1 Clustering 典型方法 1:K-means

K-means 步骤: 1. 随机给个 K 值 2. 随机选取 K 个点:ci (i=1,2,...,K) 作为 center 3. for every x in DataSet, find its cluster by evaluate distance to ci 所以 b^n_i 就相当于第 n 个样本点对第 i 个中心的权重,他的值类似于 [0,0,0,...,1,...,0] 4. update center(每一个点都是一个向量,向量之和取平均) when new x added into this cluster 注意步骤 2,不要选随即值,而是选择直接选择随即点,这样可以避免某个值可能 所有点都离他很远,这样他的 cluster 就没有任何成员,这样更新公式会造成 segmentation fault
K-means 林轩田教授讲的更好:K-means 是介于 full-RBF 和 nearest RBF 之间的一种方法
所有的样本点,应该都会在几何上对他们周围的 x 有影响,有多少影响力,就依据距离。距 离大一点的影响就少,距离小一点的影响就大。 每一个点都有一个 RBF,这个点投的票可能是-1ro+1. 新的点上要衡量的时候,就根据所有 点在这个新的点上的影响力的加权作为结果。每一个样本点都可以表达意见,每一个样本点 都是中心 跟你的新点 x,离的最近的样本点 xm 他会对结果产生最大的影响,甚至会 dominate 最终投 票结果。为什么,因为高斯函数从中心点往两边衰减的太快了。稍微远一点结果都差很多。 找到最接近的那个样本点之后,那你说啥就是啥。你说是-1,我就是-1. 让最近的 K 个人投票来决定 lazy 是什么意思?好像没有学什么东西,只是根据样本点搞事情而已。训练的时候偷懒,好 像不花什么力气,但是预测的时候,你需要花大量时间去找出来谁跟你最近等等。
1.2.2 Clustering 典型方法 2:Hierarchical Agglomerative Clustering
使用·「相似度」·「树形」和·「剪枝」概念
HAC:
build a tree(所有的样本,两两算相似度,渐次取相似度最大的两个合并,重复算最大相似度。。。)
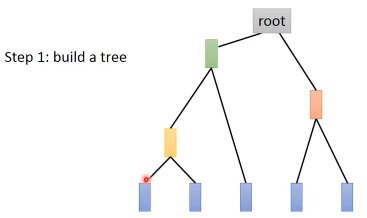
做 clustering:切一刀。
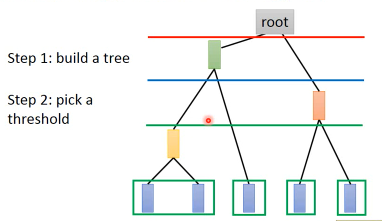 看 pdf 上红色线切出两组分类,蓝色线切出三组,绿色线切出四组分类。
看 pdf 上红色线切出两组分类,蓝色线切出三组,绿色线切出四组分类。
再次用到·「相似度」的概念,这个概念好像贯穿整个 ML
: 两个向量是否相似:inner-product : 两个分布是否相似:entropy : 自己跟自己是否相似:how concentrate : 距离非常近相似度高,否则都非常低:RBF
1.2.3 HAC 与 K-means 最大的不同:
你如何决定 cluster 的个数,K-means 很难决定 K=? HAC 不直接决定 K=? 而是通过 similarity 建立树,然后通过 threshold 决定切出多少个 cluster
1.3 Distributed Representation(一个数据点对应多个簇)
把任何一个 data 都归结为某一个 cluster,这是非常粗糙的。某个个体必须完全属于某一个 cluster 是非常粗糙的, 以偏概全, 会丢失很多信息比如工程师可能也是书法家,所以要采用·「分布式的表示方式」
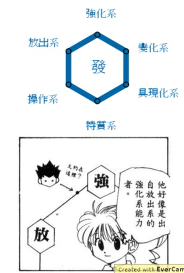
取而代之用一个 vector 来表示每个样本点: 小杰是: | 强化系 | 0.70 | | 放出系 | 0.25 | | 变化系 | 0.05 | | 操作系 | 0.00 | | 特质系 | 0.00 |
这种思想就是:Distributed representation
如果你原来的样本点是很高维的,比如图片(28*28*3) 然后用图片的某些特征来描述他,经过这种变化,就可以从高维==>低维这个过程就叫做 Dimension Reduction
Distributed representation 和 Cluster 都是不同程度的 Dimension Reduction。
1.4 Dimension Reduction
1.4.1 为什么 Dimension reduction 很有用的?
举例说明
eg1 3d 平铺
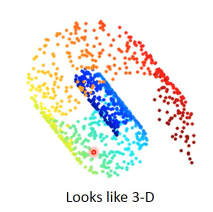
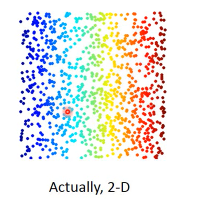 类似地毯卷起来的东西,可以平铺。不用在 3d 空间来描述。
类似地毯卷起来的东西,可以平铺。不用在 3d 空间来描述。
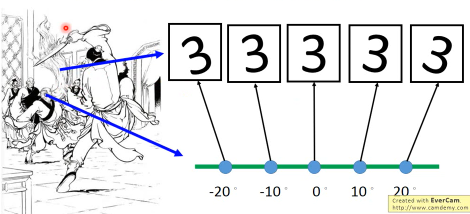
eg2 MNIST 28*28 浪费 MNIST 训练集图片都是 28*28 的向量但是这 784 维度的向量用来表示手写数字是很浪费的。因为很多位根本用不到—所有 28×28 的矩阵中只有很少一部分能形成数字。

想描述这些‘3’,一般角度而要需要 28*28*5,但如果能考虑·「旋转角度」这个图像·「特征」描述这些‘3’,只需要 28*28+1(图像的旋转角度)就可以了。 描述‘3’是不需要用这么多维度的向量的。
怎么做 Dimension reduction 呢?就是要找到某种 x-space to z-space 的 transformation,z 空间的维度 < x 空间维度

1.4.2 Dimension Reduction 最常用的两个方法:
- feature selection 如果数据集中分布在 8 个维度中的固定的 2 个维度上,就可以把其余 6 个维度去掉。但是这种方法并不一定奏效,比如·「卷地毯」那张数据分布图,就没法用。

- PCA 其实从 x-space to z-space 如果仅仅是挑选 x-space 向量的某几个维度,这就是一个线性组合而已,给 x 不同维度以不同的权重,那些权重为 0 的就是直接去掉的维度,其他的维度经过线性组合(放缩和旋转)产生某种变换,生成 z-space
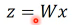
1.5 PCA: principle component analysis
1.6 PCA 怎么做呢?
z = Wx 选择不同的 W 会让 x 映射出不同的 z。
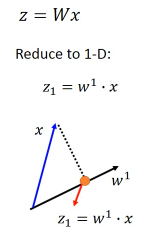
1.6.1 选择 w 的三个标准:
总结:W 就是最小化 z 差方的 row 模为 1 的 Othogonal Matrix
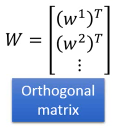
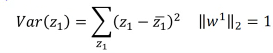
1.6.2 第一标准:row 模为 1
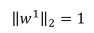 令 w 的模 为 1, 那么 w 就是一个单位向量,仅仅表示方向
w·x 的几何意义就不是相似性,而是·「x 投射到 w 方向的投影的长度」
w·x 得到的值就是在 w 这个方向上的长度
令 w 的模 为 1, 那么 w 就是一个单位向量,仅仅表示方向
w·x 的几何意义就不是相似性,而是·「x 投射到 w 方向的投影的长度」
w·x 得到的值就是在 w 这个方向上的长度
1.6.3 第二标准:最大化 z 方差
假设仅考虑 w 是二维的情况经过 z = w·x 之后,会把所有的 x 映射到 w 这条线上,得到一堆的 z。现在问题是,我要怎么选择 w 呢?目标是什么?
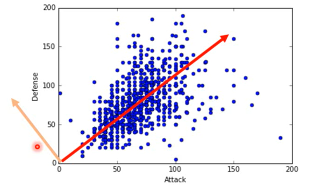
选择一个 W 经过 projection 之后,得到的 z 越分散越好。 就是经过 prejection 之后不同的样本点之间的区别度仍然保留,而不是挤在一起。 映射之后不损失原来数据的奇异度.

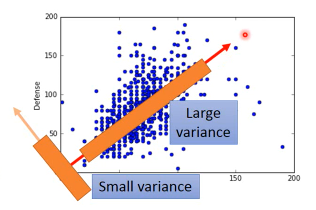
这个 w 方向,就好像一个新发掘的·「隐藏的维度」·「隐藏的特征」,这个特征与防御力和攻击力呈现某种正相关。
所以:
*选择一个 W 经过 projection 之后,得到的 z 越分散越好。* *就是经过 prejection 之后不同的样本点之间的区别度仍然保留,而不是挤在一起。* *映射之后不损失原来数据的奇异度.*
这三者都指向一个概念:variance
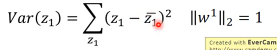 这个就是我们选择 w 的第二个标准。
这个就是我们选择 w 的第二个标准。
1.6.4 第三标准:rows 垂直
刚才说了,w 就相当于一个 ·「隐藏的维度」·「隐藏的特征」如果有多个 w,这些 w 就形成了一个·「新的坐标系」,新的坐标系就是对于原来数据点的·「新的衡量体系」,参照一般坐标系中 ·「x 轴 ⊥ y 轴」的事实,所以我们新找的每一个·「隐藏的维度」w1,w2,w3…都必须彼此垂直。这个就是我们选择 w 的第三个标准
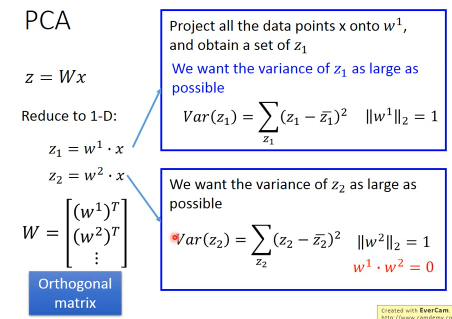
总结:W 就是最小化 z 差方的 row 模为 1 的 Othogonal Matrix 需要几个 w 向量,这个跟·「几个 hiden layer」·「几个 cluster」一样,需要经验和灵感。完全由你自己决定。
1.6.5 PCA 的数学推导
method 1 : 用线性代数+拉格朗日乘数法 method 2 : 把 PCA 描述成 NN,然后用 GD 来解
1.6.6 (一个视角)method 1 求出 w
结论是: 原来输出矩阵 X 的协方差矩阵的对应特征值最大的特征向量
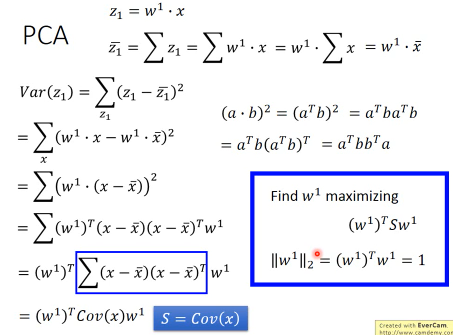



1.6.7 PCA 的另一个好处: 消去协变
做完 PCA 之后,新的 features 之间没有任何关联
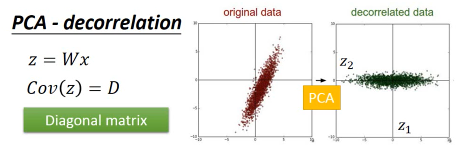
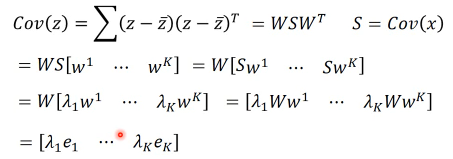
PCA 的另一个好处:decorrelation 刚才说过 W 是一个 diagonal-matrix 其实 z 的协方差矩阵,也是一个 diagnonal-matrix 下面有证明 也就是说如果今天对原始 x-space 做 PCA,原来的 data 的分布可能是上图左边那样, 两个维度不是没有关系的,而是存在一种·「正相关」的关系(请看下面的引用) 但做了 PCA 之后, 会让新的空间 z-space 的各个维度之间的 covariance=0 --> Cov(z) = Diagonal 这样的好处是,由于 x-space 的 feature 之间关联性太强,不纯粹 而 z-space 下·「另一组 feature」他们之间·「没有任何关系」,很纯粹 当你 x-space ---PCA---> z-space 时,就可以用·「另一组 feature」作为输入 代替原来的输入。这样可以大大减少你模型的参数量。你的 wb 等等参数不用再考虑·「feature 之间的关系」。 面对·「没有关系的一组 feature」就可以使用相对简单的模型,这样还可以避免 overfitting eg,你用 x-space => Generative mode Gaussian x-space ---PCA---> z-space => Generative mode Gaussian Distribution 很明显后者的参数以及计算量都会大大减少
假设 input 多个相互独立的 features 来简化概率模型: Naive Bayes
从向量上看,没有任何关系就是,两个向量的相似度为 0,那么他们应该是·「垂直的」。 从概率上看,没有任何关系就是·「独立事件」。 如果我们假设 inputpoint 的各个维度(feature)之间没有任何关系: #+DOWNLOADED: /tmp/screenshot.png @ 2017-06-07 11:52:56 [[file:Classification/screenshot_2017-06-07_11-52-56.png]] 那么,一个 K 维度高斯,就被转换成 K 个一维度高斯的乘积。这大大简化了 K 维度高斯的 Σμ 的计算。 但是这么做是有风险的,有可能损失了·「特征间关系」这一信息。让模型没法对·「正确的特征做强 有力的映射」。最后会出现 underfitting。 : 这种·「独立性假设」化简概率模型然后来做分类的方法就叫做 Naive Bayes Classifier
1.6.8 PCA 像极了 Nerual Network
PCA 的对应了 NN 的所有 hiden layers input layer 就是 x-space 的所有 features output layer 就是 针对某一个用途(分类回归) 的特定函数 x-space —PCA—> z-space
1.6.9 PCA 的数学推导还是 林轩田教授讲的好
1.7 看待 PCA 的另一个视角
这部分的讲解,也说明 PCA 跟 NN 有很多相似,或者他们的本质都是找到那个 Transformation.
在 lec-6 也有类似的对比,做手写识别之后想分析 hidenlayer 到底干了什么 于是抽取第一层隐含层的一个神经元,看训练集图片中哪些图片会让这个神经元 输出的值很大(代表神经元被激活),结果发现‘7’‘9’‘4’这三种图片都会让 神经元的输出值很大(激活),然后通过 input-layer 对该神经元的所有权重 (28×28)画在 input 图片每个维度对应的 pixel 上去,发现对应图片左上角和右下角 的 pixels 两块权重很大,所以才导致‘7’‘9’‘4’让该神经元激活。 由此想到,某一层的某个神经元就像一个·「filter」大概就负责·「过滤出某一段笔画」, 原图中这一块 pixel 不为 0(有笔记)就会被激活这个神经元(过滤)。
手写辨识数字 7, 在图形上‘7’其实是由很多基本组建组成的。就是基本的笔画,这些基本的笔画加起来就形成了一个数字。这些基本的笔画呢,就是一个个向量。把这些基本的向量加起来,就形成了一个完整的手写数字图像。这种表示方法,是远远比用像素级别来表示要‘节省’的多。
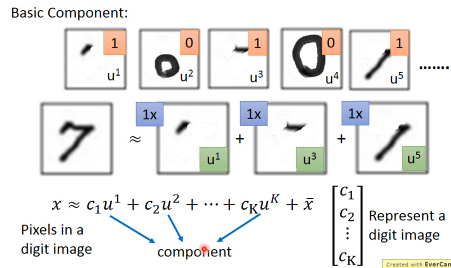
u1 u2 u3 u4 u5 u6
/ --- | \ | /
| /
| /
------------------------------------
1 1 0 0 0 1
------------------------------------
/----/
/
/ = 1*u1 + 1*u2 + 0*u3+ 0*u4 + 0*u5 + 1*u6
/
-> c = [1,1,0,0,0,1] 就是每个 basic component 的 weight
所以一个 6 维度向量,远比 28×28 维度向量要‘节省’的多。
1.7.1 (另一个视角)method 1 求出 w
把·「肢解后的‘7’还原」与·「‘7’原图」之间的差距叫做·「Reconstruction Error」
 这里加上 x 的平均 也很好理解,就是为了·「过滤超过平均灰度的像素」所以事情就变成,
我要找 K 个 basic component,来最小化 预测结果和真实值 之间的差距
把上面的目标直接丢到 loss-fn 中交给 Model 自动执行出结果就好了。
这里加上 x 的平均 也很好理解,就是为了·「过滤超过平均灰度的像素」所以事情就变成,
我要找 K 个 basic component,来最小化 预测结果和真实值 之间的差距
把上面的目标直接丢到 loss-fn 中交给 Model 自动执行出结果就好了。



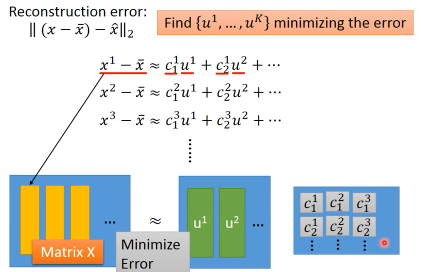
TODO,从上图和下图可以看出 c 矩阵可以通过 ΣV 来得到,为什么下面还要用 ck = (x-x~)·wk 呢?
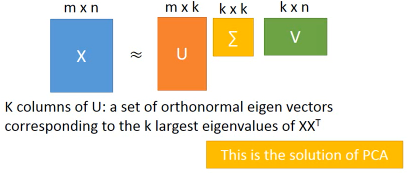
所以按照这种思想求得的结果跟用·「线性代数+拉格朗日」的结果是一致的:新的 component(新坐标系下的每个点的 features) 就是 原来输出矩阵 X 的协方差矩阵的对应特征值最大的特征向量
1.7.2 (另一个视角)method 1 求出 c
根据之前的讲解: z-space = {span of w1,w2,…,wk} 想要最小化·「Reconstruction Error」就是让 c·W 与 x-x~ 尽可能接近
 c·W 是什么?其实就是 c 向量在 W 平面(也就是 z-space)的投影,由于 W 平面(z-space)是由
w1,w2,…,wk span 而来。那么 w1~wk 就是 z-space 的基本坐标系。所以 c·W 也就可以看成 c 向量 在 w1~wk 方向上投影(c1,…,ck)的向量的和。所以只要 x-x 平均 映射到 w1~wk 的分量与 c 向量 映射到 w1~wk 的分量(c1…ck)
分别相等即可。
c 向量的每个维度,都等于 x-x~ 在 w1~wk 的投影
c·W 是什么?其实就是 c 向量在 W 平面(也就是 z-space)的投影,由于 W 平面(z-space)是由
w1,w2,…,wk span 而来。那么 w1~wk 就是 z-space 的基本坐标系。所以 c·W 也就可以看成 c 向量 在 w1~wk 方向上投影(c1,…,ck)的向量的和。所以只要 x-x 平均 映射到 w1~wk 的分量与 c 向量 映射到 w1~wk 的分量(c1…ck)
分别相等即可。
c 向量的每个维度,都等于 x-x~ 在 w1~wk 的投影
1.7.3 用 Neural Network 来表示 PCA : Autoencoder
用 NN 实现 PCA 必须要用(另一个视角)才能实现 PCA looks like a neural network with one hidden layer (linear activate function) – This is Autoencoder
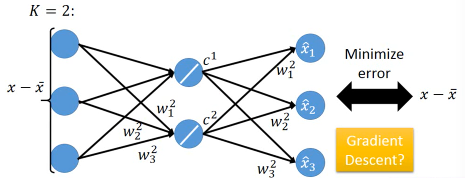
>>>用 GD 和 用数学的不同 ------------------------------------------------------------------ 但是当·「只有一层隐含层时」使用 GD 是·「不能保证 w1~wk 相互垂直」,之前证明过了 只有 w1~wk 相互垂直时,才能保证·「reconstruction error 最小」。所以用 NN 来表示的 PCA,然后用 GD 来获得一个解,但不是最佳解。 ------------------------------------------------------------------
因为 PCA 是 linear 的 dimension reduction,如果仅仅考虑 linear 的情况 autoencoder(NN 版的 PCA)是不合适的,但是如果考虑 non-linear 的 dimension reduction。autoencoder 可以变成 deep-autoencoder 显然。deep-autoencoder 更好。
autoencoder 不仅仅可以只有一层 hiden layer,也可以 deep。 autoencoder –> deep autoencoder
1.8 PCA 的弱点

Unsupervised: 因为 PCA 是 unsupervised,所有没有 label 来标明映射是否合理如 ppt 图一,一对点其实内含了某种分类,如果不考虑这个因素,PCA 做的结果就会让黄蓝亮色完全混在一起。完全没发做分类-—分类信息丢失。
这个时候需要考虑 LDA(教授没有深入讲解), LDA 考虑了内部带有分类的 dimension reduction, 他是 supervised。
linear disciminent analysis
- Linear: S 型曲面我们想降维,最好的方法是需要拉直,但是 PCA「不是拉直」,而是「打扁」因为 PCA 只能做 linear dimension reduction
1.9 PCA 例子
1.9.1 eg1:PCA pokemon
我该把原始样本 project 到多少维度更合适呢?这个需要根据你的问题来决定。想做 visualization 比如数据点都是 6 维的,你没法观察,所以想投影到 2 维,这样就可以观察了。不过有一些常用的方法:

- 计算每一个 component 的 lambda:每一个 principle component 都是一个 eigen-vector,我现在要计算的就是他们各自对应的 eigen-value.
- 计算每一个 eigen-value 的 ration eigeni's ratio = lambdai/(sum all lambdas) ratio 代表什么呢?ratio 越小说明原始空间做 projection 时,这个 eigen-vector 的贡献越小—没有太多信息的。
- 从 ratio 大到小,选择 Priciple Component
·「注意」eigen-value 是什么,就是代表 X(x-sapce inputs) 的 covariance eigen-value: λ 就代表了映射之后是否足够分散,因为 PCA 的重点就是选取较大的 eigen-value 对应的 eigen-vector.
实际分析如果从 ratio 选择前四个,这新的坐标系,物理意义是什么?
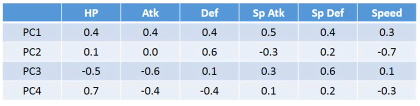
6 个原始通过某种权重 W 映射到 4 个维度。 (x1,x2,x3,x4,x5,x6) —>W—> (z1,z2,z3,z4)
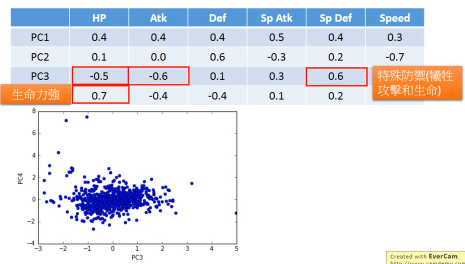
- 可以看到,PC1(新坐标轴 1) 那一行对应的 ·「原始属性」都是正的,这可以代表 pokemon 的·「强度」 - 可以看到,PC2(新坐标轴 2) 那一行对应的 ·「特殊攻击和速度」负的,【防御力是正的】,这可以代表他用 牺牲·「特殊攻击和速度来换取防御力」 - 其他每行都可以按此推导 可以看到利用 PC4 PC3 来画坐标图,其【整体点的分布呈现椭圆形】,也就是两者是 decorelation 的 整体点分布呈椭圆形 ===> 坐标轴(feature)decorelation. 现在,原始空间中的样本点,就从原来的(x1,x2,x3,x4,x5,x6) ---> (z1,z2,z3,z4) 也因为他们的这层关系,所以也可以他们看成是 每给 z1 增加 z1,就相当于给原始坐标系下每个坐标轴增加这么多 z1 = 0.4x1 + 0.4x2 + 0.4x3 + 0.5x4 + 0.4x5 + 0.3x6 | | | | | | | v v v v v v v 2*(z1) = 0.8x1 + 0.8x2 + 0.8x3 + 1.0x4 + 0.8x5 + 0.6x6 所以如果 z 那一行的 wij 出现负值代表什么: z2 = 0.4x1 - 0.4x2 + 0.4x3 - 0.5x4 + 0.4x5 + 0.3x6 | | | | | | | v v v v v v v 2*(z2) = 0.8x1 - 0.8x2 + 0.8x3 - 1.0x4 + 0.8x5 + 0.6x6 增加 z2 就会让负的更小,正的更大,代表我以牺牲 x2,x4 为代价换取 x1,x3,x5,x6 的增长 1. wij 正的增加,负的减小 2. wij 越大的增加和减小的越快 3. 如果某一行的 wij 出现异号,可以看成某种 tradeoff
1.9.2 eg2 手写辨识
把上面的定义应用到手写辨识 MNIST 上是什么意思呢?把每一张数字图片都拆成:component weight * component
eigen-digit 如果画前 30 个 component,

把手写 9 进行 PCA,取前 30 个 lambda 最大的 PC,其实每一个也都相当于一个小图片。也许是纹理,也许是 9 的一部分,等等。给这 30 个 PC 一个名称叫"eigen-digits"
1.9.3 eg3 人脸辨识
eigen-face

给这 30 个 componentes 一个名称叫"eigen-face"
教授提出:为什么这里的 eigen-face eigen-digit 不是某种「肢解」而是好像
整体的一种「滤镜」。
因为这些 PC 不止可以相加,还可以相减。先生成一个 8,然后·「减去」下面的圈再·「加上」
一个 1。这是可以的。
而且根据之前的那个矩阵可以看出来,他每一个 PC1~4 上的增减,其实也都对应原来图片
整体的某种增减。
所以 PCA 是一种·「滤镜」式的 dimension reduction 所以 NMF 是一种·「肢解」式的 dimension reduction,
NMF(non-negative matrix factorization)
肢解和滤镜的形成原因
滤镜的形成原因是 weights 和 component 可以是正的 or 负的
肢解的形成原因是 weights 和 component 必须是正的
1.10 MF: matrix factorization
NMF on MNIST

强迫所有 PCi(新的坐标系) 都是正的,也就要求必须是某种·「叠加」。强迫所有 weight 都是正 or 零,也就是某种·「部分」每一个人跟他所喜欢的公仔是有某种关系的,所以他选择去买的公仔不是随机的。
有人萌傲娇的,有人萌天然呆的 。
每一个公仔在动画中也都有傲娇和天然呆的(傲娇和天然呆都是 factors)。
两者存在·「相似性」时才会购买
是有些 common latent factors 来决定【购买行为】
所以我们可以通过统计某些人买的公仔来形成一个 matrix
但是,是否只有傲娇和呆两种属性呢? 不一定。这就像 PCA 的维度和 NN 的层数一样,要去试一试,需要事先决定好的。
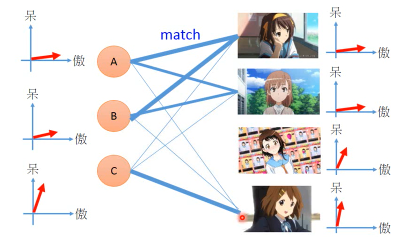
但是這些 feature(呆 傲娇) 是没办法直接获得的
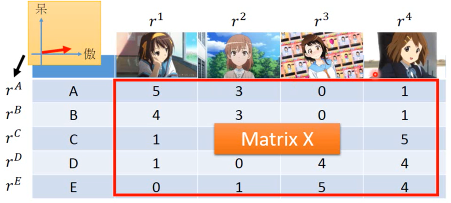
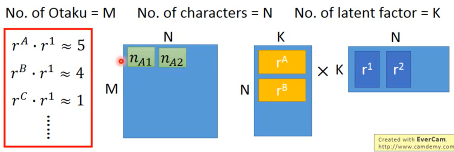
公仔角色数量 = N, 买家数量 = M, 衡量特征 = K | | Toy1_1 | Toy2_1 | Toy3_1 | Toy4_1 | | | Toy1_2 | Toy2_2 | Toy3_2 | Toy4_2 | | | . | . | . | . | | | . | . | . | . | | | Toy1_k | Toy2_k | Toy3_k | Toy4_k | |--------------+--------+--------+--------+--------| | a1 a2 ... ak | 5 | 3 | 0 | 1 | | b1 b2 ... bk | | | | | | C1 c2 ... ck | | | | | | d1 d2 ... dk | | | | | | e1 e2 ... ek | | | | |
做一种假设,所有的 matrix 位置都是由兩個 vector 做内积得到的
所以我们的目标就是找一组 rA rB… 找一组 r1 r2… 让他们的内积与这个矩阵的差距最小。
这个东西就可以用 SVD 来解。 Matrix = SVD 但是,这里是兩個矩阵,怎么办? Matrix = (SV)D or Matrix = S(VD) 如此即可。
1.10.1 处理【数据缺失】问题
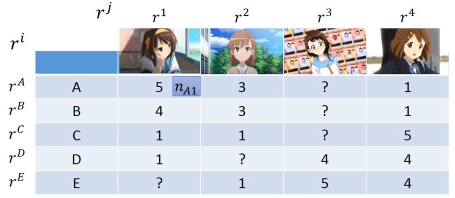 面对这种缺失数据的表格该怎么办呢?这里就肯定不能用 SVD 了,SVD 要求一个完整的矩阵所以我们仍然可以做,但是需要一种不使用矩阵的优化算法---Gradient Descent
可以只往 GD 中填充已有的数据
面对这种缺失数据的表格该怎么办呢?这里就肯定不能用 SVD 了,SVD 要求一个完整的矩阵所以我们仍然可以做,但是需要一种不使用矩阵的优化算法---Gradient Descent
可以只往 GD 中填充已有的数据
SVD 需要矩阵 是数学解
GD 不需要矩阵 是近似解
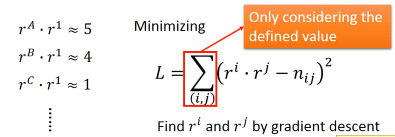

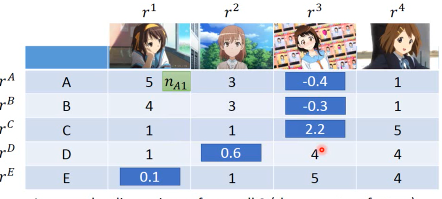
但是如果遇到一些 missing 值怎么办,比如遗漏了对(E, Toy1)的统计。 1. 用已经有的值去估算出这样的 latent-vector 2. 用 gradient 来做最小化 3. 然后再用得到的 latent-vector 去估算 missing value
1.10.2 更精确的假设
Considering the individual characteristics
 难道购买手办仅仅是因为性格相仿,还有其他因素么?
bA(买家) : 买家就是喜欢买公仔,跟买家性格无关
b1(角色) : 这个角色有多惹人喜欢,跟角色性格无关
难道购买手办仅仅是因为性格相仿,还有其他因素么?
bA(买家) : 买家就是喜欢买公仔,跟买家性格无关
b1(角色) : 这个角色有多惹人喜欢,跟角色性格无关
加入这两个个体属性之后,衡量相似性的方式就发生了改变,也就是改变了 ML 三步骤
中的 step-2 : goodness of fn. 也就是影响了 loss-fn 所以 loss-fn 也要
改。
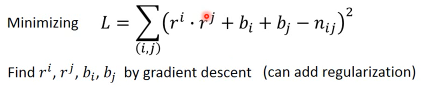 这样更精确,可以用 GD 直接解,或者也可以加上 regularization
【注意】李老师这里给出了关于 L1 regularization 应用场景的经典描述:
这样更精确,可以用 GD 直接解,或者也可以加上 regularization
【注意】李老师这里给出了关于 L1 regularization 应用场景的经典描述:
如果你希望结果 ri,rj 比较 sparse ,也就是说【结果非黑即白】没有中间地带, 要么就萌傲娇要么就萌天然呆,不会有模糊的人,这时候就加入 L1 regularization 虽然本质上 regularization 是对 weights 进行操作,以达到让【最小化】考虑 一些对 weight 的限制,但是这里也可以用, _可以把 ri,rj 互相理解为对方的 weights_ regularization 是要通过【微分】来展示其如何限制 weight 的: L1: 导致 GD 在更新 w 时【按量减少】 - 对特别大的 w 减少的慢 - 对特别小的 w 减少的快 L2: 导致 GD 在更新 w 时【按比例减少】 - 对特别大的 w 减少的快 - 对特别小的 w 减少的慢 所以 L1 导致 w 处在两端(大的维持大,小的会更小) ****_________** 所以 L2 导致 w 处在中间(大的很快小,小的维持小) ____*********__
Ref: Matrix Factorization Techniques For Recommender Systems
MF 还有其他应用:
1.10.3 MF 用在 topic analysis: LSA
角色 - 文章买家 - 词汇
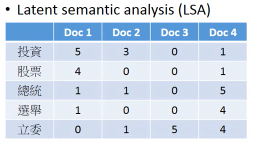
如果我希望不是均等的考虑所有词汇,该怎么做呢?
就给某些重要的词汇加上更高的权重, weighted by inverse document frequency 权重加在 loss-fn 中,这样某个词汇错误的影响就会比其他词汇更大。
为什么是 inverse frequency 呢?一些常用的非信息词汇:'是' ‘如何’ ‘处理’这些词汇在·「每篇文章中都高频出现」,那么他肯定属于·「公众词汇」,这样的词汇不能充分表现文章的·「独特性」,所以肯定权重就低。反之亦然。
常见的 LSA 变种:PLSA,LDA(Latent Dirichlet allocation)
·「注意」 在 ML 有两个 LDA 经常提到:
- Latent Dirichlet allocation (文档分析,三层概率分布)
- Linear discriminant analysis (类似 PCA 但是 supervised)
1.11 LDA: linear discriminent analysis
线性判别分析
1.11.1 回忆 PCA
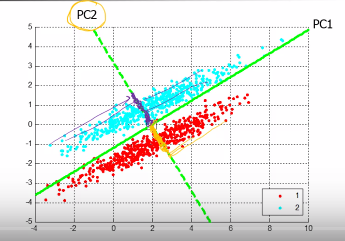 PCA 不认为 PC2 重要,他认为 PC1 更重要,因为 PC1 让点散布的更开(covariance 更大)
PCA 的两个缺点:
PCA 不认为 PC2 重要,他认为 PC1 更重要,因为 PC1 让点散布的更开(covariance 更大)
PCA 的两个缺点:
- Unsupervised
- Linear
PCA 的目标:投影之后的点,散布的越开越好 – 最大化 z 的方差
1.11.2 LDA 与 PCA 的不同
LDA 对同一堆数据的分析是这样的:
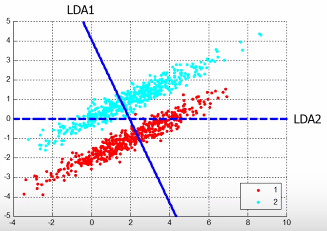
1.11.3 LDA 的目标
LDA 找到的轴不要求像 PCA 一样(w1,w2,w3 相互垂直),LDA 找到的轴找到的新的坐标系不用相互垂直希望投影之后:
- 类间距大:投影之后各个 class 的中心(mean)距离越大越好
- 类内距小:投影之后的样本到投影之后的中心要很近
所以 LDA 找的点是:·「最大化类间距」·「最小化类内距」·「最大化类间距」 — Between-Class Scatter Matrix
S_bLDA = ΣPimimiT - mmT Maximize eT(S_bLDA)e
·「最小化类内距」 — Within-Calss Scatter Matrix
S_wLDA = ΣPimimiT - mmT Minimize eT(S_wLDA)e
Some Notations of LDA

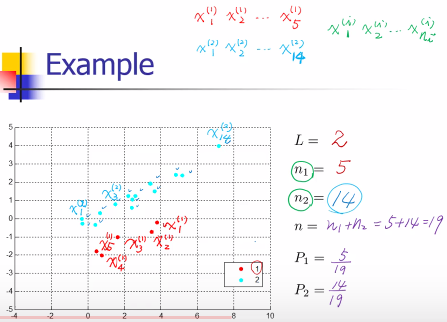
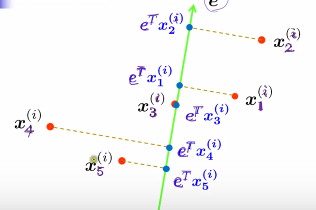
Projections
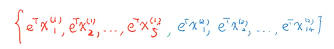
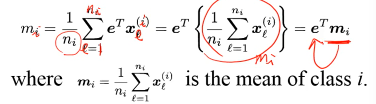 所以投影的中心,也就是中心的投影
mi' = eTmi
(上面的公式写法跟图片不一样,意思一致)
所以投影的中心,也就是中心的投影
mi' = eTmi
(上面的公式写法跟图片不一样,意思一致)
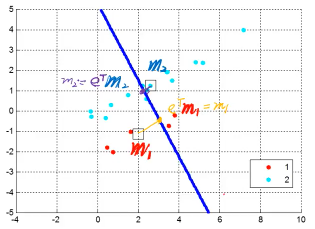 所以希望投影之后,eTm1 与 eTm2 差越大越好
所以希望投影之后,eTm1 与 eTm2 差越大越好
1.11.4 Between-Class Scatter Matrix
The sum of square-distances between class-means 「最大化类间距」就用·「最大化类中心的之间的距离和」
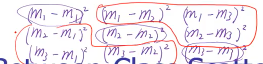
三个分类要计算的所有距离每一个差距都被算了两次,所以需要除以 2

一个 ML 中经常使用的转换
注意这里的一个·「特别有用的转换」: 平方变成内积 (eTmi - eTmj)^2 = (eTmi - eTmj)(eTmi - eTmj) = (eTmi - eTmj)(eTmi - eTmj)T 因为(eTmi - eTmj)是一个常数,所以 scala 的转置还是自身
如何理解 ΣΣ
每个点的中心想减之后得到各种 mi-mj 然后
所有的 mi-mj 组成了一个向量,这个向量与自身的装置的内积就是 ΣΣ() 这个
式子的结果。
也可以把 ΣΣ 理解成两层循环,而循环的对象就是 ΣΣ()里面的东西
两个 ΣΣ 放在一起可以表示矩阵,而里面的元素就是 ΣΣ()括号里的东西
L
Σ Pi
i=1
|--------------------------------
L ||pipj(mi-mj)(mi-mj)T | | |
Σ pj || | | |
j=1 || | | |
 SbLDA 是衡量什么的,其结果也是一个 covariance
是 covariance(类中心之间距离)
SbLDA 是衡量什么的,其结果也是一个 covariance
是 covariance(类中心之间距离)
这个 SbLDA 也叫 Between-Class Scatter Matrix (分散矩阵)
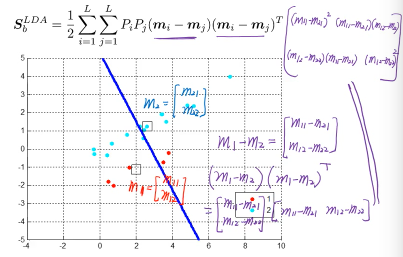
其实两两之间拉开,还有一种表达方法:计算出所有类的中心的中心
然后·「最大化类中心的之间的距离和」 就变成 ·「最大化每个类的中心到所有点的中心的距离和」
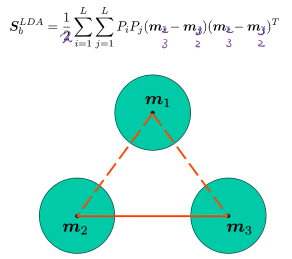
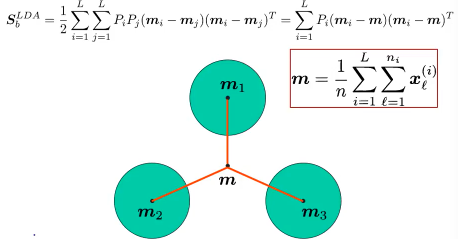
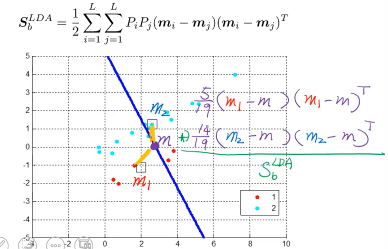
可以证明·「最大化各类之间的距离和」与「各类中心到全数据中心的距离和」是相等的

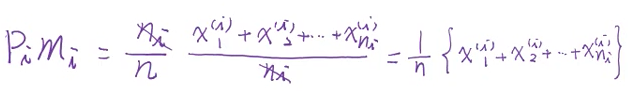
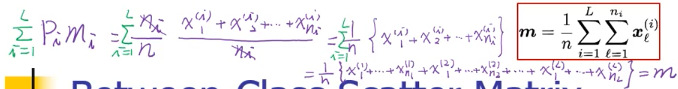
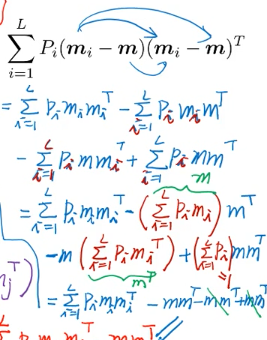
所以最后·「各个类的中心到所有数据的中心的距离」化简之后就是:
S_bLDA = ΣPimimiT - mmT
这个公式很 intuition
1.11.5 Within-Class Scatter Matrix
Weighted sum of all class-variances ·「最小化类内距」 就是最小化 weighted sum of all class-variance
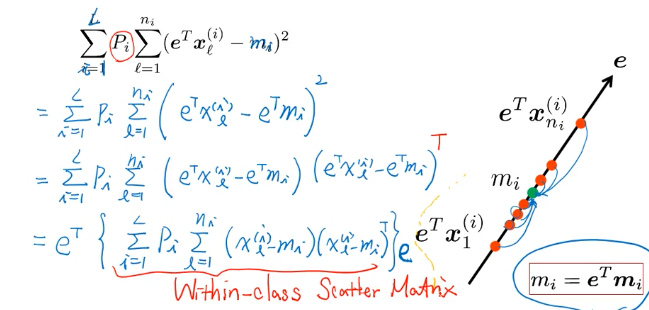
这个像什么,就像是 PCA 的最大化目标,PCA 是·「所有点力求映射之后的散布越大越好」这里 LDA 的两个目标中的最小化内距的目标是 「某类点力求映射之后的散布越小越好」
1.11.6 总结两者,为优化做准备

1.11.7 优化:Rayleigh Quotient
怎么调整这个映射 e, 使得同时 类间距最大 类内距最小 这种两个相反方向的最佳化问题,经常使用除法表示

要求最大化的这个 quotient 叫做 Rayleigh Quotient


Generalized eigen decomposition =====> Matrix*向量 = λ*向量这个是之前学得是 普通 eigenvalue problem.但是,这里的是 =====> Matrix1*向量 = λ*Matrix2*向量这个叫做 Generalized eigenvalue problem
注意,Generalized eigenvalue problem 找出的 eigen-vector 不是相互垂直的
·「工程上」的做法是等式两边同时乘以 SwLDA 的逆矩阵这样可以转换成 普通的 eigenvalue problem
这样之后同 PCA 一样也是求出 ·「最大 eigenvalue 所对应的 eigenvector」这个就是 e
1.12 很多的 Dimension reduction 方法
- MDS(multidimensional scaling)不需要把每个样本都表示成 vector,只需要两个样本之间的距离 MDS 跟 PCA 是有关系的,PCA 有一个特性是,他保留了原始点的距离在高维空间中接近,低维空间也会接近。一般教科书举出的例子都是:我有兩個城市,但是我不知道怎么把城市表示成向量, 我就可以用 MDS 因为他只要【兩個样本之间的距离】
- Probabilistic PCA (probabilistic version of PCA)
- Kernel PCA (non-linear version of PCA)
- CCA(Canonical Component Aanalysis) 如果你有两个 source,声音,图像,这两种不同的 source 都做 dimension reduction 这就是 CCA
- ICA(Independent Component Aanlysis) PCA 是找 othoganal component, ICA 是找 independent component
- LDA(linear discriminant analysis)—supervised
1.13 Demystifying Dimensionality Reduction
https://www.youtube.com/watch?v=YzqjassagUQ 这个视频很不错
也是在这里才发现:有很多 Matrix Decomposition 方法:
- LU Decomposition
- QR Decomposition
- Eigen Decomposition
Singular Value Decomposition
--------------------------------------------------- PCA method-1 使用了 eigen decomposition PCA method-2 使用了 SVD --------------------------------------------------- MF 使用了 SVD (matrix = (SV)D or S(VD)) (预测缺失值 GD) --------------------------------------------------- LDA 使用了 Generalized eigen decomposition ---------------------------------------------------