lec-22 Structured Linear Model

1. Structured Linear Model

1 Structured Linear Model

>>> 神之三问：

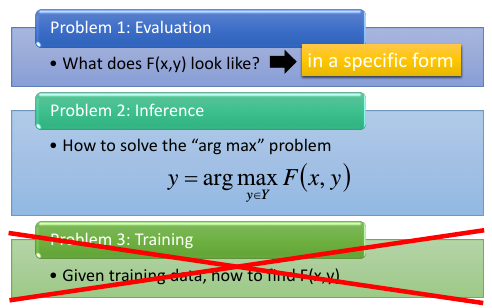
• Evaluation: What does F(x,y) look like? • Inference: How to solve the “arg max” problem • Training: Given training data, how to find F(x,y)

如果第一个问题表示成一个特殊的形式，那么第三个问题就不是问题。

1.1 Structure Linear Model: problem 1

用 DL 获得 Φi 注意如何获得 Φ 呢？

其实 DeepLearning 的 hiden-layer 不就是 feature extractor 么之前讲过的。

Φ1(x,y) 表示 xy 具有特征 1 的强度 scala; Φ2(x,y) 表示 xy 具有特征 2 的强度 scala; …

Φ(x，y) = [Φ3(x,y), Φ2(x,y), Φ3(x,y)…] vector.

可以把每一个 Φ 都理解成一个 F 的分量，只不过这些分量之间是线性组合的关系： F(x,y) = w1•Φ1(x，y) + w2•Φ2(x，y) + w3•Φ3(x，y)… w1,w2,w3… 是要从 training data 中学到的

如果第一个问题表示成一个特殊的形式，那么第三个问题就不是问题。

举例说明，这个公式的具体意思：

1.2 eg1, Object Detection

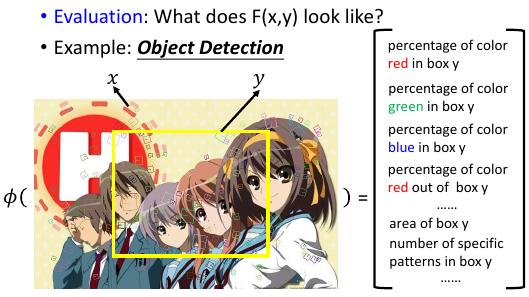在 bounding-box 这个例子中， x is image; y is box; Φi is 自己找的一些 x,y 匹配的特征：

percentage of color red in box y
percentage of color green in box y
percentage of color blue in box y
percentage of color red out of box y
……
area of box y
number of specific patterns in box y
……

1.2.1 visual word as a Φi

注意图中有些【大大小小的不同颜色的方块】，这叫做 pattern 一个小方块就是一个 pattern, pattern 就像是文章中的词汇一样。也叫做 visual word. 一般这么描述：在这个方框里面编号是 100 号的 visual word 出现幾個。他也是一个维度的 featuren:Φi

问题：這些 visual word 是要自己找呢？还是可以自动生成？因为这是个线性模型，我们是没办法做太复杂的事情，想提高效果，你要抽出很好的 feature.

1.2.2 用 DL 获得 Φi

那怎么抽取 feature 呢？像上面那些我们自己找的 x,y 匹配 feature 不一定是好的，这里可以用 CNN 来做。 CNN 的 input 是 image, output 就是一个 vector,而这个 vector 可以很好的代表这个 bounding-box 里面的东西。

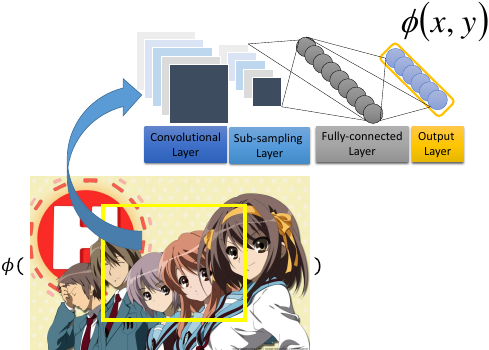
bounding box 是没法用 DNN 来做的，因为 DNN 怎么会知道 box 应该框在哪里。所以一般 object dectection 都是用 DNN + structure learning 来做的。

所以抽取 feature 是可以用 deep learning 来做。可以把所有的 hiden-layer 都理解成是对 input-layer 数据的某种 feature extraction 转换，最后输出给 output-layer 的是抽取之后的 features.

1.3 eg2, Summarization

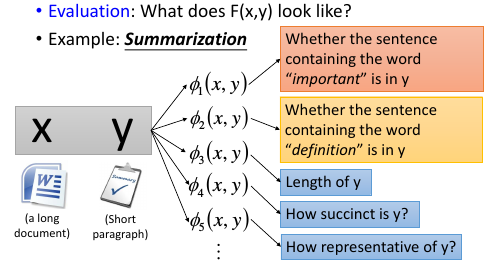
1.4 eg3, Retrieval

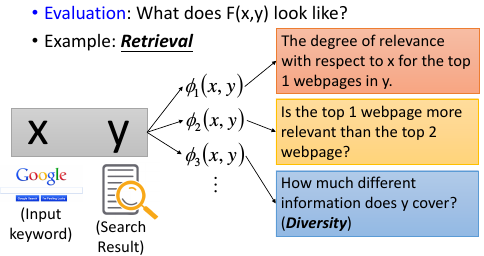
1.5 Structure Linear Model: problem 2

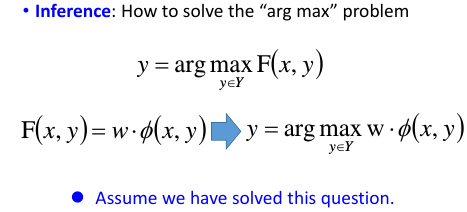如果第一个问题定义好了，下面怎么办呢？ [假装]已经被解决了，这里没弄懂李老师想干什么，他没有讲这个

1.6 Structure Linear Model: problem 3

希望找到一个 w 使得以下条件被满足：

对所有训练数据，希望正确的 xr,yr 得到的 w•Φ > 大于其他所有的 xr,y 得到的 w•Φ

举例说明：

1.6.1 eg1, Obejct Dectection

框对的图片的向量的打分 > 框错的图片的向量的打分

之前说过 Φ(x,y) 是一个 vector, F(x,y) = w•Φ(x,y) 换句话说，每一个 x1-image,y1-box 都有一个对应的 Φ(x1,y2) 他是一个 vector ,也就是一个【点】。

Φ(x1,y1) = Φ(iamge,box) = 一个点

现在有两个【正确】 boxed image 也就是两个【正确】处理过的图片，也就是（x1,y¹），（x2,y²）

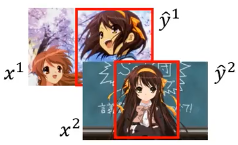
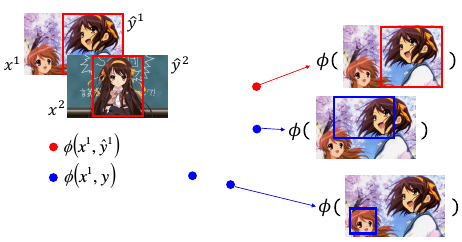
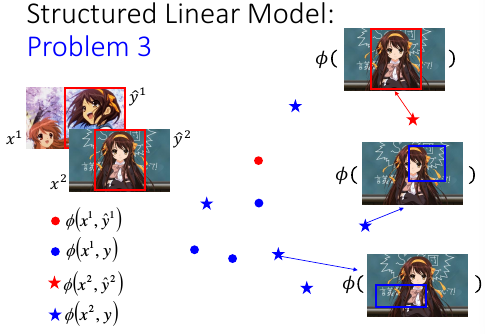
1.6.2 如何把 structure 数据变成 vector 数据

>>> 经过处理的图片 —Φ—> 点 >>> structure —Φ—> vector

Φ(x1,y1) = Φ(iamge,box) = 一个点

现在有两个【正确】 boxed image 也就是两个【正确】处理过的图片，也就是（x1,y¹），（x2,y²）

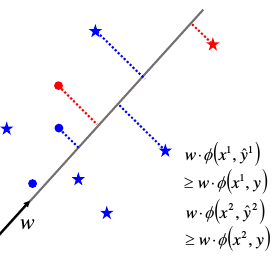
对于 (x1,y¹) 通过 Φ 转换之后形成红色● Φ(x1,y¹) 对于 (x1,瞎吊框) 通过 Φ 转换之后形成蓝色● Φ(x1,瞎吊框)

那么红色点会只有一个，而蓝色点有无数多个。

对于 (x2,y²) 通过 Φ 转换之后形成红色★ Φ(x2,y²) 对于 (x2,瞎吊框) 通过 Φ 转换之后形成蓝色★ Φ(x2,瞎吊框)

那么红色点会只有一个，而蓝色点有无数多个。

1.6.3 寻找让正确处理的图片打分最高的 w

x 图片 (x,y) 处理过的图片Φ(x,y) 处理过的图片的某些特征的向量 F(x,y) = w•Φ(x,y) 处理过的图片的某些特征的向量的打分现在处理过的图片都表示成了向量，下面我要做的就是进一步给所有的向量【打分】，分数最高的就是【框对的】，其他的都是【瞎吊框】，如何打分呢？

内积是什么，是向量夹角，向量相似性，也是映射

打分就是把 Φ vector 内积到 w 上

找到这样的 w 同时让

w•Φ(x1,框对的) > w•Φ(x1,瞎吊框)

w•Φ(x2,框对的) > w•Φ(x2,瞎吊框)

亦即框对的图片的向量的打分 > 框错的图片的向量的打分

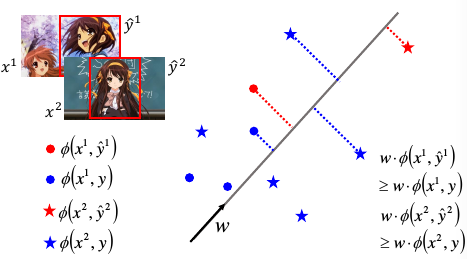注意 w 的方向很重要，他指明了【正】的方向

1.6.4 解决 problem-3 的算法

这个算法跟轩田老师的 perceptron 算法基本一致

- x1  表示 第一张未 box 的图片
- y^1 表示 给第一张图正确 box
- y1  表示 第一张图的所有 box 方法
- y*1 表示 能最大化打分的 box 方法

1. 我有一堆正确 boxed-images: {(x1,y^1),(x2,y^2),(x2,y^2)...}
2. 初始化 w0 = 0
3. do {
       挑出（下）一个图片，计算出【处理后的图片的向量的打分】 wi•Φ(x1,y1)
       这里 y1 有无限多个－－瞎吊框有无限种方法，所以这个分数也有无限多个
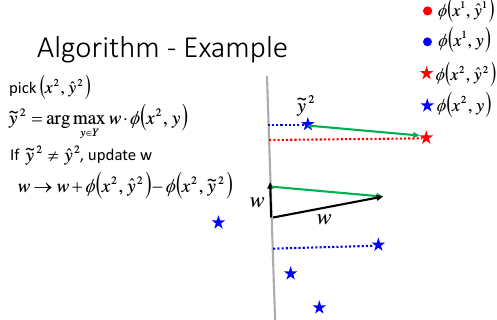
       找出其中能让 wi•Φ(x1,y1) 最大的那个 y*1（这一步就是 problem-2,我们先假设他已经完成了）
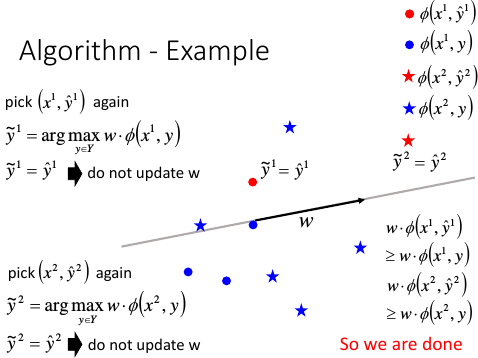
       比较 y*1 与 y^1
       如果 y*1 ≠ y^1, 则更新 w = w + Φ(x1,y^1) - Φ(x1,y*1)
      } until (w can not be updated by all images)