lec-12 Semi-supervised Learning
Table of Contents
1 Semi-supervised Learning
Outline
- Semi-supervised Learning for Generative Model
- Low-density Separation Assumption
- Smoothness Assumption
- Better Representation
半监督模型的核心问题是:如何把不带标签的数据,合理的变成带标签的数据

有 labeled-data 和 unlabeled-data. 且 无标签数据远远多余有标签数据两种 semi
- Transductive learning: unlabeled data is the testing data
- Inductive learning:unlabeled data is NOT the testing data
labeled data 很少 unlabeled data 很多所以需要 semi-supervised learning

虽然无标签数据是没有标签的,但是无标签数据的分布,暗含了·「某种信息」半监督学习通常需要·「某种假设」, 半监督学习是否能 work,也很依赖你做出的这些·「假设」·「假设是否符合实际」·「假设是否足够精确」
1.1 Supervised Generative Model
1.1.1 回忆监督学习下的生成模型

但是如果今天除了 有标签数据 还给你很多 无标签数据,结果就会发生变化 就会影响你对‘这件事情’的感觉
1.1.2 Semi-Supervised Generative Model
淡绿色点是 unlebeled data
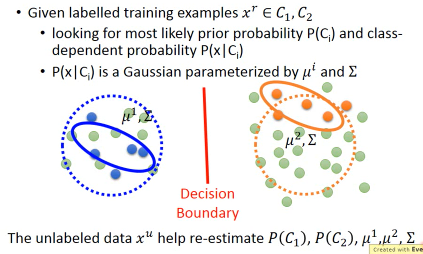
这些绿色的点会影响你对两个 gaussian(μ1,μ2,Σ)的估测, 也就是影响了 P(c1),P(c2)的估测进一步影响 P(x|ci) 的估测进一步影响 P(ci|x) 的估测最终影响了影响了你的 Decision Boundary
直觉上是上面这样,真正的算法如下:
1.1.3 EM algorithms

先初始化必要参数θ={P(c1), P(c2), μ1, μ2, Σ}
可以根据 labeled data 得到 θ进而算出 Pθ(c1|xu)
[E]:算 prior 概率:P(c1) μ1
回忆监督学习下的生成模型怎么算 P(c1) 的: P(c1) = N1/N ===> 就是用所有标记为 c1 的样本 除以 总样本数现在必须考虑那些 unlabeled-data 可以把 P(c1) = N1/N 看成 P(c1) = ΣP(c1|xr)/N = N1*100%/N 所以同理也可以这么处理 unlabeled-data P(c1) = ( ΣP(c1|xr) + ΣP(c1|xu) )/N 半监督模型的核心问题是:如何把不带标签的数据,合理的变成带标签的数据 这里 P(c1|xu) 可以看成:这个 unlabeled-data point 可以被看成几个 c1-data point, 半个,1/4 个 那么 ΣP(c1|xu) 可以看成:所有 unlabeled-data point 可以被看成几个 c1-data point Pθ(c1|xu) 可以由步骤 1 算出
回忆监督学习下的生成模型怎么算 μ1 的:利用 maximum likelihood 算出 Gaussian(μ,Σ) 最可能产生所有 c1 数据的 gaussian:最后得到:μ1 = average(all xr in c1) 现在必须考虑那些 unlabeled-data 套用跟 P(c1)计算相同的思路: c1 data point unlabeled-data point μ1 = c1 中 xr 的和/c1 的样本数 μ1 = c1 中 xr 的和 / c1 的样本数 + xu * 可以被看成几个 c1-data point/ 所有 unlabeled-data point 可以被看成几个 c1-data point μ1 = Σxr / N1 μ1 = Σxr / N1 + Σxu * P(c1|xu) / ΣP(c1|xu)
- [M]:把 step2 的 P(c1) μ1 带入 step1 中得到新的参数θ1
理论上这个方法会收敛,但是初始值会影响收敛的速度,类似 Gradient-descent
实际上 step2 is 'E' of EM algoritm 实际上 step3 is 'M' of EM algoritm
1.1.4 EM 算法背后的理论是什么
Why? 回忆 Generative-model labeled-data 分类法算法
后验 = 条件×先验 / 现象 这是我们做分类的标准生成模型公式。
- 首先根据每个标签各自的样本数比例算出先验概率
- 最有可能搞出 c1(c2,c3…)样本的高斯:根据 ·「最大似然法」 估计出每个标签对应的最有可能产生各自样本的高斯分布(μ1,Σ1)(μ2,Σ2)(μ3,Σ3)
- 最有可能搞出所有样本的高斯:假设所有高斯分布共用一个 Σ, 再次根据 ·「最大似然法」 算出各自样本的高斯分布(μ1,μ2,μ3…,Σ)
- 根据新的高斯分布(μ1,μ2,μ3…,Σ),算出 条件概率和现象概率
- 根据标准公式算出 后验概率
 现在 Generative-model labelled and unlabeled-data 分类法算法
现在 Generative-model labelled and unlabeled-data 分类法算法
step 1,2,3,4 都要改变,前面已经介绍了 1,2 如何改变
现在 ·「最大似然法」 也要改变:
每一个 unlabeled-data 都要最大化其成为每一个标签的概率。每一个 labeled-data 都只最大化其 标签的概率。
Maximum likelyhood with labelled data: logL(θ) = ΣlogPθ(xr,yr) Maximum likelyhood with labelled and unlabeled data: logL(θ) = ΣlogPθ(xr,yr) + ΣlogPθ(xu)
labeled and unlabeled-data : Pθ(xu) = Pθ(xu|C1)P(C1) + Pθ(xu|C2)P(C2) labeled-data : Pθ(xr, yr) = Pθ(xr|yr)*P(yr)
但是下面这个公式不是 convex 的,所以要 solved iteratively Pθ(xu) = Pθ(xu|C1)P(C1) + Pθ(xu|C2)P(C2) 所以前面的 EM 算法,每次循环就是要让 Likelyhood 增加一点直到他收敛到某一个 local maxima
这里没搞懂,logL(θ) = ΣlogPθ(xr,yr), Pθ(xr, yr) = Pθ(xr|yr)*P(yr)和下面讲的不一样(lec-4) 尤其是 Pθ(xr, yr) = Pθ(xr|yr)*P(yr) 这里,似乎对应的是步骤 4 的公式?
下面的公式,是用 MLE(maximum likelyhood estimation)来找出某个标签(Water 系神奇宝贝)的最好的 Gaussian 的过程但是这里并没有
* P(yr)这一项
而且在最后(对应步骤 4)的 modifying model 中也没有出现
* P(yr)
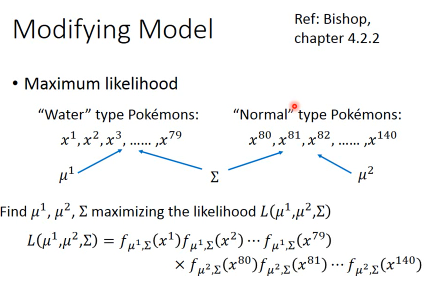
1.2 Semi-supervised learning low-density separation
假设有一大堆 data,两个 class 之间有非常明显的‘鸿沟’, 一个非黑即白的世界。 low-density separation 是说在两个 class 的分界面数据分布非常的稀疏,几乎是空白的没有数据的。

*半监督模型的核心问题是:如何把不带标签的数据,合理的变成带标签的数据* Generative mode 会把 不带标签的数据 变成 0.3,0.4,0.8 个带数据的标签 self-traing 会把 不带标签的数据 变成 0/1 个带数据的标签 前者叫做 soft-label 后者叫做 hard-lbael
1.2.1 Self-training
基于非黑即白的算法最典型的就是 self-training

- 只用 labeled-data 训练出一个 f*
- 然后用 f* 去给 unlabeled-data 分类(打标签)
- 用·「启发式算法」把一些打过标签的数据添加到 labeled-data 中
- 回到步骤 1
注意,self-training 的假设是·「边界上数据稀疏」。只有在这个假设前提下, self-training 才 work。所以对于 regression 问题,这个算法是很难奏效的。而且 regression 的输出标签是 实数。这个标签对于更新 f*是完全没有任何帮助的。
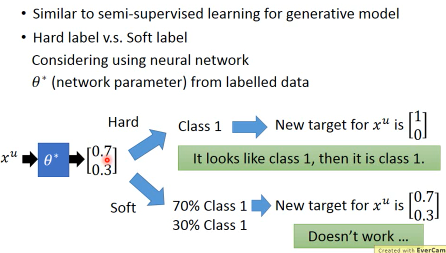
self-training 有一些类似刚才的 半监督生成模型方法区别是:
- Hard label: self-training 强制指定 unlabeled-data 必须属于某一个标签
- Soft label: generative model 的 unlabeled-data 会概率性的属于每一个标签
哪个更好呢:对于 NN 来说,方法 1 可行,方法 2 肯定不行,为什么呢?
通过方法 1,得到这个 xu 的 输出(是概率向量[0.1,0.4,0.5]), hard-label 就会认为是[0,0,1], xu 变成一个 xr(x,c3),然后你可以用这个 xr,作为 NN 的输入,然后得到一个 概率向量输出,然后算他们俩的 entropy。这个没什么问题。
通过方法 2,得到这个 xu 的 输出(是概率向量[0.1,0.4,0.5]), soft-label 就是用这个概率向量重新给 xu 打标签, 这完全没有 任何意义,用这个点作为输入得到的概率向量肯定还是这个[0.1,0.4,0.5]。训练不出任何东西。
1.2.2 Entropy-based Regularization

刚才那一招的进阶版:看到[0,0,1]就认为他是 c3 这样太武断了。用这种方法把 unlabeled-data 变成 labeled-data 再用 Lossfn去进化参数,这样做得到的参数未必好。因为如果输出是[0.3,0.3,0.4]把他当作[0,0,1]的 labeled-data 就太不负责任了。换一种角度也就说明这个模型(以 NN 为例)并没有把这个 unlabeled-data ·「转换成足够区分度的数据」,如何改进呢?
加入 regularization,这个 regularization 既不是 L2 也不是 L1而是针对这种‘可能性太分散’做出的修正 — entropy(对于某种信息分散性的度量)
Regularization 就是用来修正 loss-fn 的: L = ΣC(y,y') ===> L = ΣC(yr,yr') + λΣE(yu) yu 是 unlabeled-data 的输出,一个概率向量[0.3,0.4,0.3] E(yu) 就是计算这个向量和自己的 entropy。 E(yu) = - Σ yu*ln(yu)
两个向量是否相似:inner-product 两个分布是否相似:entropy 自己跟自己是否相似:how concentrate
这里提供了一个思路,教我们如何·「针对实际情况」来创造·「domain-oriented loss function」如果我想要一个·「区分度较高」的结果,就加·「高区分度的逆向函数」进 loss function 去让他自动的最小化。
如此一来,似乎机器学习的模型成了·「另一个具备自动执行能力的电脑」,一个大型 loop 语句,退出循环的条件就是 loss-function,你只需要按照你的意愿修改 loss-function 不用问什么,这个‘loop’就会自动给你需要的结果。
1.2.3 outlook:semi-supervised SVM
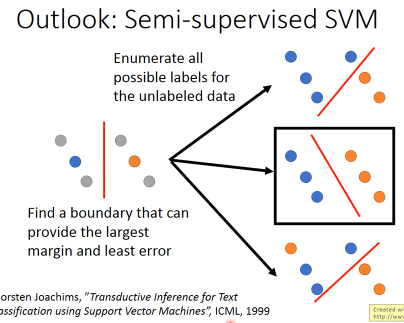
另一个很著名的算法, 半监督 SVM穷举每一个 unlabeled data 属于每一种分类的情况,在所有可能中找出·「令 margin 最大」·「令 error 最小」的那种。穷举太慢怎么办?每次选一笔 unlabeled-data,变成 labeled-data,看看是否会让 margin 变大且 error 变小。也是一种循序渐进的方法
1.3 Smoothness Assumption(high density path)
精神是:近朱者赤,近墨者黑
如果两个 x 是相似的,那么他们的 label 也应该相同。
精确的解释:
- x 的分布是不平均的
- 如果 x1 x2 在某个高密度区域中距离很近,那么他们的 label 应该相同
他们可以用 high density path 做 connection
假设这个是我们 data 的分布
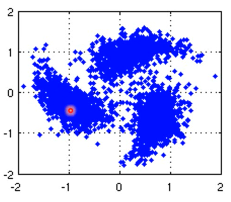
同时我们有三笔 data,x1,x2,x3,从距离上看,好像 x2,x3 的 label 应该比较像但是, smoothness assumption 的假设是·「要通过一个 high density region」来‘像’ x1,x2 之间有一个 high density region. 或者说他们俩是通过一个 high density path connect 起来的。所以这个符合 smoothness 假设,所以 x1,x2 的 label 应该相似。而 x2 x3 之间没有 high density path connect 他们,所以 x2,x3 的 label 没有相似。
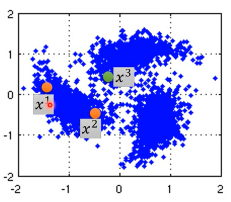
1.3.1 smoothness assumption 为什么 work?
三个例子:手写数字识别/人脸识别/文档分类
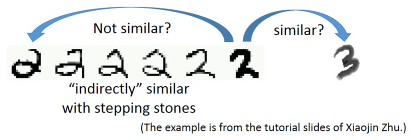
1.3.2 eg. handwriting recognition
从左边的 2,到中间的 2,再右边的 3.
从外形上看,中间的 2 跟右边的 3 可能比较相似,但是如果数据量很大,就会有从左边的 2 到中间的 2 的各种类似·「某种连续变换」的各种 2.这可以视为某种 high density path, 一组·「中间过度的形态」所以 左边的 2 和中间的 2 属于同一个标签。

1.3.3 eg. humanface recognition
人脸辨识其实也是一样的,
1.3.4 eg. 文档分类会更有用
比如要分类:天文学和旅游文章
天文学文章有固定的 word distribution
旅游学文章有固定的 word distribution
某些文章已经知道是天文学文章,他们就是 labele-天文学 data
某些文章已经知道是天文学文章,他们就是 labele-旅游学 data
如果你的 labeled-data 与 unlabeled-data 有很多重叠的单词,那么就可以很容易的处理这些问题,如下图

但是真实情况下,文章之间并不存在词汇重复,因为文章量很大,很难出现这种情况,词汇非常 sparse 的,重复 word 的比例非常小。
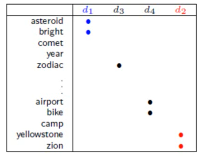
但是如果你收集到足够多的 unlabeled-document他们机会呈现出类似前面手写和人脸识别的某种·「某种连续变换」·「中间过度的形态」
 这样存在·「high density path」的两篇文章就可以被分到一类,而如果这一类中有一个是 labeled-document, 那么另一篇文章就也属于这一类。
这样存在·「high density path」的两篇文章就可以被分到一类,而如果这一类中有一个是 labeled-document, 那么另一篇文章就也属于这一类。
1.3.5 Cluster and then lable
怎么实现这个 smoothness function 呢?
蓝色--unlabeled data
橙色--class 1
绿色--class 2
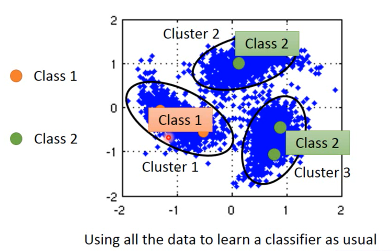
- 先把所有的 data 做 clustering
- 某个 cluster 中,哪一类标签的 data 最多,这整个 cluster 就属于那类 label 但是这种方法未必有效,因为有时候很难把·「同一个 class 的东西,cluster 在一起」
作业三,是可以用 self-training 的 但是用 cluster and then lable 就不 work.
尤其是在 Image 里面,想把同一个 class 的东西,cluster 在一起就更难了。
之前一节有说过机器学习经常要处理一些 Complex Task :不同的 class 可能会长的很想,同一个 class 可能会长的很不像。把相似的东西分成不同类,把不同的 东西分成相同的类。 单纯只用像素级做 clustering,是很难做的(不同的 class 可能会长的很想,同一个 class 可能长的很不像) 你没法把·「同一个 class,cluster 在一起」, label 就没有意义,label 的也是错误的标签所以你如果想用 cluster and then label 你的 cluster 必须要很强,你要有很好的方法来·「描述」你的 Image。 一般用 deep auto-encoder 来抽取 feature,然后在做 clustering,这样才会 work
1.4 Graph-based Approach
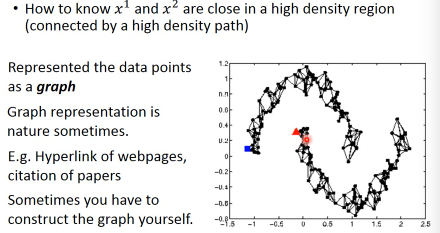
刚才的做法是比较直觉的做法来实现:smoothness assumption 另外一個做法是引入 graph structure 我们用 graph structure 来表达
connected by a high density path我们把所有的 data points 放在一起建成一个 graph 每一个 data 就是 graph 的一个 node 你要想办法建立 edge,也就是 similarity of data
建成 graph 之后,就可以说如果今天有两个点在这个 graph 中是·「相连」的,那么他们就是
connected by a high density path只有·「相连」才算·「connected」就算距离近但是不相连,也不算 connected
怎么做这个图呢?
有时候这个图是很自然就可以想到的
eg,今天要做网页分类 你有记录网页和网页之间的超链接,那·「超链接」自然的就告诉你这些网页间是如何 连接的。 eg,论文分类 论文与论文之间有引用的关系,这个·「引用」也是另外一种连接 这两种情况都可以很自然的画出这个图 有时候这个图需要你自己想出来
1.5 Graph Construction
Graph 的好坏对结果的影响是很严重的 Graph 的建立通常依赖经验跟直觉。
建立图的步骤:
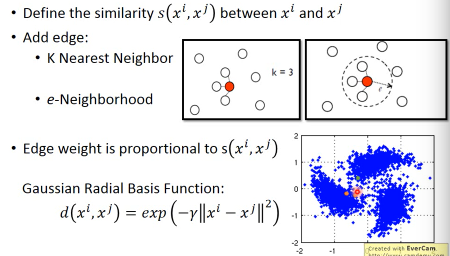
1.5.1 1. 定义如何计算两个 data 之间的相似度
影像如果直接用 pixel 算相似度,表现不太好 如果用 deep auto-encoder 算相似度,表现还不错. 怎么定义相似度呢? 推荐使用
RBF function: s(xi,xj) = exp(-γ * ||xi-xj||^2)
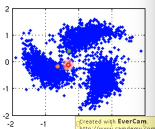
为什么 RBF 要用 exp 呢?因为这样做模型的表现会很好,因为没有 exp 的话,这个公式变化的太均匀,加上 exp 之后,只有当 xi,xj 非常近时,最后结果 (similarity) 才会大,接近 1.只要他们稍微‘远’一点 similarity 就会非常小。也就是说只有距离相当的近才会获得较大的 similarity,稍微远一点如途中黄点和浅蓝点的 similarity就非常的小. 只有这种机制才能避免做出·「跨海沟,但是距离近」的连接.
两个向量是否相似:inner-product 两个分布是否相似:entropy 自己跟自己是否相似:how concentrate 距离非常近相似度高,否则都非常低:RBF
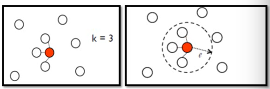
1.5.2 2. 算完相似度之后,就可以添加 edge 了
添加边的方法有很多种: K nearest neighbor,每个点都与·「相似度(来自 step1,不一定是距离)最高的」K 个点连线 e-neighbor ,每个点都与·「周围相似度超过某个 threshold e」的所有点连线
1.5.3 3. 连和不相连(0/1),还可以标注 weight
weight 需要跟 两个点之间的相似度(by step1)保持正比
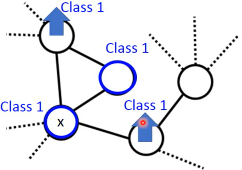
1.5.4 Graph 方法的核心思想:近邻 + 传染
紧挨某个 class 的点,被分成这个 class 的概率会上升,而且这种上升会·「传染」
- The labelled data influence their neighbors
- Propagate through the graph
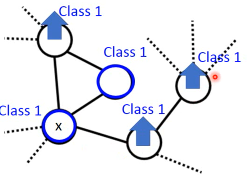
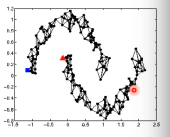
1.5.5 Graph-based 方法的弊端:
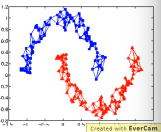
数据量要求较高之前文档分类已经提到过,要收集的信息必须是·「一种连续渐进的变化」这就是说基于图的方法要求数据量要高质也要高。否则就变成:

这种情况就是信息没有·「传染过去」,没有找到·「循序渐进变化的数据」
1.5.6 定义平滑度(smoothness)
刚才是讲如何定性的使用 graph,现在要讲如何定量的使用 graph
- Define the smoothness of the labels on graph 定义标签有多符合我们给予的 smoothness 的假设(平滑度)比如下面的两个图都一样,唯一不同的是给予了 data 不同的标签感觉上来说左边的 label 更 smooth 一些,但是如何定量描述 smooth 呢?
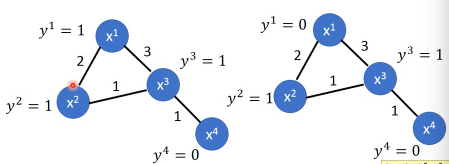
smoothness = 求和(所有相连的节点的标签的平方 × 边的权重)
 TODO : 这里为甚么是 'for all data (no matter labelled or not)'
那些没有无标签点的 y 值怎么算呢?
TODO : 这里为甚么是 'for all data (no matter labelled or not)'
那些没有无标签点的 y 值怎么算呢?
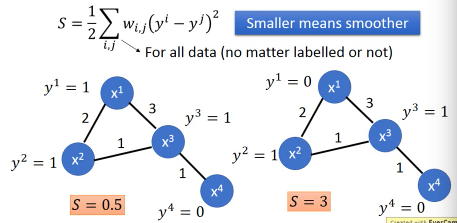 Sl = 1/2 * (2*(1-1)2+
3*(1-1)2+
1*(1-1)2+
1*(1-0)2) = 0.5
Sr = 1/2 * (2*(1-0)2+
3*(0-1)2+
1*(1-1)2
1*(1-0)2) = 3
Sl = 1/2 * (2*(1-1)2+
3*(1-1)2+
1*(1-1)2+
1*(1-0)2) = 0.5
Sr = 1/2 * (2*(1-0)2+
3*(0-1)2+
1*(1-1)2
1*(1-0)2) = 3
注意:相邻点只算一次距离,不是 yi-yj,yj-yi
1.5.7 简化 smoothness 公式
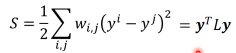 稍微整理一下,把 y 串成一个 vector,总共 R+U 维度
y = […yi…yj…]
稍微整理一下,把 y 串成一个 vector,总共 R+U 维度
y = […yi…yj…]
L:就是 graph laplacian (这里还会用到:Laplacian Eigenmaps )
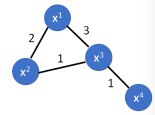
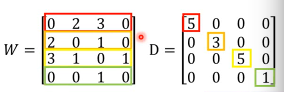
L = D - W W 是一个对称矩阵,是两两 data 之间的 weight D 是一个对角矩阵,把 W 的每一个 row 加总起来作为每一个对角位置的值
1.5.8 深入理解化简后的 smoothness 公式
S = yTLy 这个 y 是 label TODO , 为什么 yTLy 是 depending on NN parameters 没搞懂
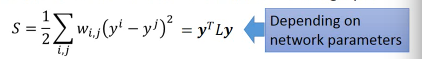
 所以我们可以通过修改 Loss-fn 来获得更 smooth 的 label
所以模型不仅要 ·「获得最小的 error」还要·「获得最好的 smoothenss」,越 smooth 值越小这个怎么解呢,还是用 GD
所以我们可以通过修改 Loss-fn 来获得更 smooth 的 label
所以模型不仅要 ·「获得最小的 error」还要·「获得最好的 smoothenss」,越 smooth 值越小这个怎么解呢,还是用 GD
这个 loss-fn 是很经典的,在以后的学习中会经常用到:他在一个 loss-fn 中统合了【监督学习 loss】和【非监督学习 loss】
cross-entropy 是典型的 监督学习的损失函数 smoothness 是典型的非监督学习的损失函数
半监督学习损失 = 监督学习损失 + 非监督学习损失
这个似曾相识啊:<来自之前的笔记>
加入 regularization,这个 regularization 既不是 L2 也不是 L1 而是针对这种‘可能性太分散’做出的修正 — entropy(对于某种信息分散性的度量)
Regularization 就是用来修正 loss-fn 的: L = ΣC(y,y') ===> L = ΣC(yr,yr') + λΣE(yu) yu 是 unlabeled-data 的输出,一个概率向量[0.3,0.4,0.3] E(yu) 就是计算这个向量和自己的 entropy。 E(yu) = - Σ yu*ln(yu)
>>> 相似性 similarity
两个向量是否相似:inner-product 两个分布是否相似:entropy 自己跟自己是否相似:how concentrate
这里提供了一个思路,教我们如何·「针对实际情况」来创造·「domain-oriented loss function」如果我想要一个·「区分度较高」的结果,就加·「高区分度的逆向函数」进 loss function 去让他自动的最小化。
如此一来,似乎机器学习的模型成了·「另一个具备自动执行能力的电脑」,一个大型 loop 语句,退出循环的条件就是 loss-function,你只需要按照你的意愿修改 loss-function 不用问什么,这个‘loop’就会自动给你需要的结果。
1.5.9 smoothness 注意事项(TODO,没理解)
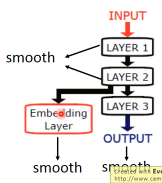
算 smoothness 不一定要在 output-layer,可以是某个 hiden-layer 算 smooth,也可以是每一个 hiden-layer 都算 smooth
1.6 Looking for better representation
去芜存菁,化繁为简这个会等到 unsupervised learning 再讲解简单说下精神:
- Find the latent factors behind the observation
- The latent factors(usually simpler) are better representations
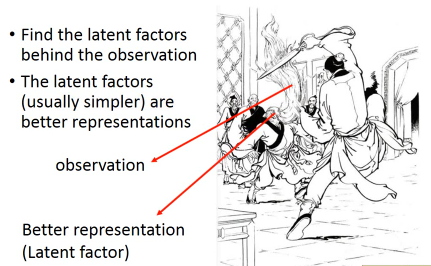 胡子变化多端,但是仍然需要依靠头
胡子变化多端,但是仍然需要依靠头