lec-15 Neighbor Embedding
Table of Contents
1 Neighbor Embedding
做的事情就是非线性版本的 PCA 降维 Manifold Learning 很近的距离的情况下,欧几里得距离才会成立,如果相距很远欧式距离就不成立了
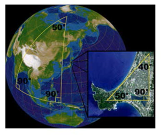
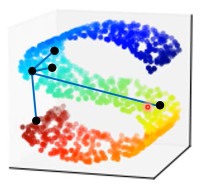
在高维空间中,算欧式距离可能就没有意义了比如上面淡蓝色部分的点,欧式距离上与红色点更近,但是从分类角度讲【循序渐进式】的变化才是更近的。高维空间中的【欧式距离】就像【虫洞】一样不可捉摸让人想到,semi-supervised learning 中的一个假设 Smoothness Assumption(high density path)
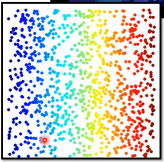 但是,如果我们可以把高维空间的点的分布【铺平---非线性降维】,这个时候就可以使用【欧式距离】了。 不论是接下来做 supervised learning 还是 clustering 都大有帮助
但是,如果我们可以把高维空间的点的分布【铺平---非线性降维】,这个时候就可以使用【欧式距离】了。 不论是接下来做 supervised learning 还是 clustering 都大有帮助
非线性降维有很多方法:
1.1 LLE: locally linear embedding
1.1.1 我想使用欧式距离
似乎这个 LLE 的终极目标就是【能使用欧式距离】这样就可以用之前【线性空间】中的很多算法了有一组点,先选出某个 xi 的 neighbor 然后边的权重就是 xi 与 neighbor 的【相似性】的某个正比数据:wij
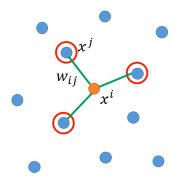
如何找到这个 wij 呢?
1.1.2 共用 wij
我们希望,每一个 xi 都可以用他的 neighbor 通过 linear combination 组合而成所以要用最小化 xi 与 xi'(用邻居模拟出的值)来约束 wij,并求出 wij
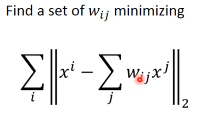
有了这些,就可以来做 transformation 了,也是找到一个转换从 卷轴 到 平铺从 x-space 到 z-space 从 xi,xj 到 zi,zj 唯一一点不同的是:xi 与 xj 的关系 wij 也必须是 zi 与 zj 的关系。
这就好像白居易的《长恨歌》一样:临别殷勤重寄词,词中有誓两心知,七月七日长生殿,夜半无人诗已迟,在天愿作比翼鸟,在地愿为连理枝,天长地久有时尽,此恨绵绵无尽时。
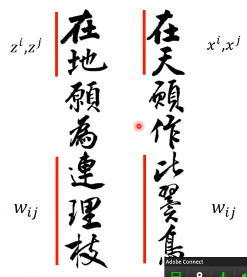
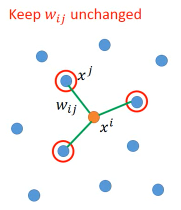 也就是说,原来的 xj 可以通过 linear combination 产生 xi.
现在我希望做了 dimension reduction 之后地 zi 也可以通过 zj 用相同的权重来产生。
也就是说,原来的 xj 可以通过 linear combination 产生 xi.
现在我希望做了 dimension reduction 之后地 zi 也可以通过 zj 用相同的权重来产生。
所以这衍生出 LLE 的一个优点:
优点:就像 MDS 一样,你可以只用 wij 就获得 zi,zj 而不用知道 xi,xj
缺点:注意 LLE 并不像 autoencoder 一样可以找出一个明确的 function 把原来的 x –> z
1.1.3 调整邻居的数量
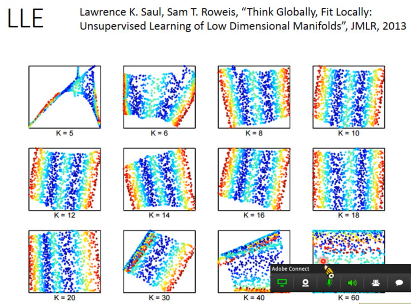 LLE 要好好调整你的 neighbor 才能获得好的结果---不同的 k(num of neighbor)
k 太小效果不好,太大效果也不好。为甚么太大效果也不好呢?因为之前讲过,【欧式距离只在距离较近时有效】,如果你选取的 neighbor 太多就有可能已经选到【很远的】neighbor, 这样在 transform 前后就 hold 不住。
LLE 要好好调整你的 neighbor 才能获得好的结果---不同的 k(num of neighbor)
k 太小效果不好,太大效果也不好。为甚么太大效果也不好呢?因为之前讲过,【欧式距离只在距离较近时有效】,如果你选取的 neighbor 太多就有可能已经选到【很远的】neighbor, 这样在 transform 前后就 hold 不住。
1.2 Laplacian Eigenmaps
1.2.1 Graph-based approach
(like semi-supervised, smoothness assumption – high density path) 就是说你在高维空间中算兩個点的欧式距离没意义,要算【他俩在高密度路径上】的距离给 wij 设置一个 threshold ,如果 wij 超过这个 threshold 就把两者 connect 起来
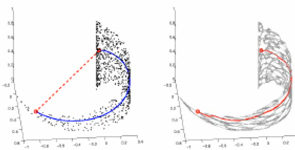
1.2.2 近似距离
所以如果你想知道高维空间中两点的距离,就先做图,把大于阈值的两点连线起来,然后高维空间中的【两点的距离】,就是铺平后【兩個点之间路径的距离之和】这是一种近似距离,因为路径肯定时弯弯曲曲的。
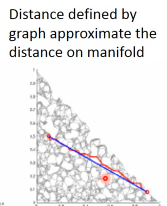
1.2.3 那些假设
回忆 semi-supervised learning 如何把没标签的点转化成有标签的点
【如果 x1,x2 足够近,那么 y1,y2 一样】

同样的道理可以被用在 unsupervised learning — Laplacian Eigenmaps 中
【如果 x1,x2 足够近,那么 y1,y2 一样】 ==========> 【如果 x1,x2 足够近,那么 z1,z2 足够近】
 但是,这里由于没有 监督学习损失函数的【辅助】 所以,不能直接使用 S 作为损失函数,所以要手动加上一个限制:
if the dim of z is M, Span{z1,z2,…,zn} = RM
但是,这里由于没有 监督学习损失函数的【辅助】 所以,不能直接使用 S 作为损失函数,所以要手动加上一个限制:
if the dim of z is M, Span{z1,z2,…,zn} = RM
加上这个限制之后呢,可以得到他跟 semi-supervised with smoothness assumption 的结果恰好【相反】,他得到的 z 恰好是 L(S = yTLy) 的对应的较低 eigen-value 的 eigen-vector
1.2.4 副产品:Spectral Clustering
如果你用上面得到的 z 做 cluster,这就是 spectral cluster (光谱聚类)
1.3 t-SNE
T-distributed Stochastic Neighbor Embedding 【T-SNE】作业四会用到
1.3.1 更严格的假设
前面只假设了【如果 x1,x2 足够近,那么 z1,z2 足够近】而没有假设: 【如果 x1,x2 足够远,那么 z1,z2 足够远】
类内聚集,类间分散
这个也跟 LDA 的要求很像
LLE on MNIST 会出现这样的问题:
 他确实会把不同类型的点聚集在一起 ===> 相似不同类的点映射之后足够近但是他没有做到把同类型的点分散开 ===> 不同类的点相互重叠
他确实会把不同类型的点聚集在一起 ===> 相似不同类的点映射之后足够近但是他没有做到把同类型的点分散开 ===> 不同类的点相互重叠
1.3.2 与 LDA 比较
----------------------------- 极似 LDA 不过 LDA 是 supervised t-sne 是 unsupervised t-sne 一般用来做 visulization LDA 一般用来做 降维 -----------------------------
1.3.3 损失函数

1. 上面公式里的 [*] 是其他所有的 datapoint 2. KL 表示 KL divergence 3. 用 GD 来解 L --------------------------------------------------------- 1. t-SNE 的问题是也就是所有点的 similarity,计算量很大。 2. 虽然他也是降维但是代价略高,一般都是先用较快的方法 PCA 把 x 降到 50 维, 然后再用 t-sne 把 50 维度降到 2 维度。 3. t-sne 是没办法 on-line 的,必须事先给定数据集,因为要算各个点之间的 similarity 所以 t-sne 通常是做 _visualization_
1.3.4 计算相似性
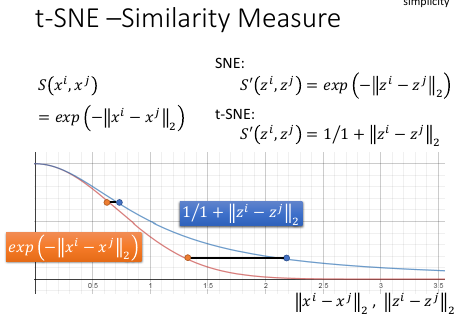
------------------------------------------------------- PCA 用 RBF 函数来算 similarity SNE 用的也是 RBF t-SNE 神妙的地方在于,他在 映射前后选择的 similarity 是不一样的 -------------------------------------------------------
他在做了 dimension reduction 之后选择的 similarity 是 t-distribution 中的 一种,t 分布中有参数,可以调整他。为甚么要这么做呢?
>>>如果映射之后你要维持他原来的几率(他们的相对关系)的话,就变成如下函数图形 >>>如果黄色两点原来的距离较大,映射之后蓝色兩點的距离会被拉大 >>>同样可以想象, >>>如果黄色两点原来的距离很近,映射之后蓝色兩點的距离也会很近
对 pixels 做 PCA 降维之后做 t-SNE 的图,手写识别(MNIST)右边扭曲的圈圈是什么意思呢?没听懂【qqqq】
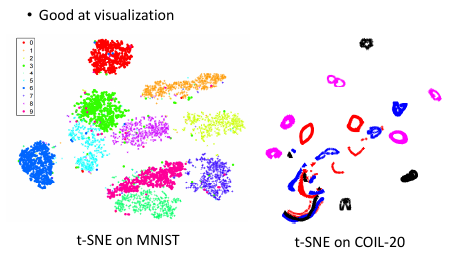
1.3.5 可视化效果
这个图展示了 t-SNE 做可视化的效果非常好

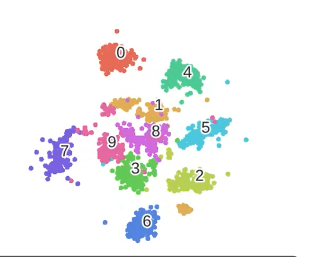
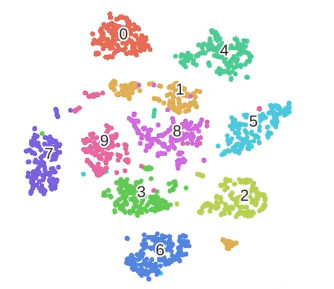
符合类内聚集,类间分散的要求
1.4 Reference
To learn more …
- Locally Linear Embedding (LLE): [Alpaydin, Chapter 6.11]
- Laplacian Eigenmaps: [Alpaydin, Chapter 6.12]
- t-SNE
- Laurens van der Maaten, Geoffrey Hinton, “Visualizing Data using t-SNE”, JMLR, 2008
- Excellent tutorial: https://github.com/oreillymedia/t-SNE-tutorial